人教版数学 八年级下册 第18章 平行四边形 培优训练含答案
文档属性
| 名称 | 人教版数学 八年级下册 第18章 平行四边形 培优训练含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 431.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 21:17:31 | ||
图片预览

文档简介
人教版
八年级下册
第18章
平行四边形
培优训练(含答案)
一、选择题(本大题共4道小题)
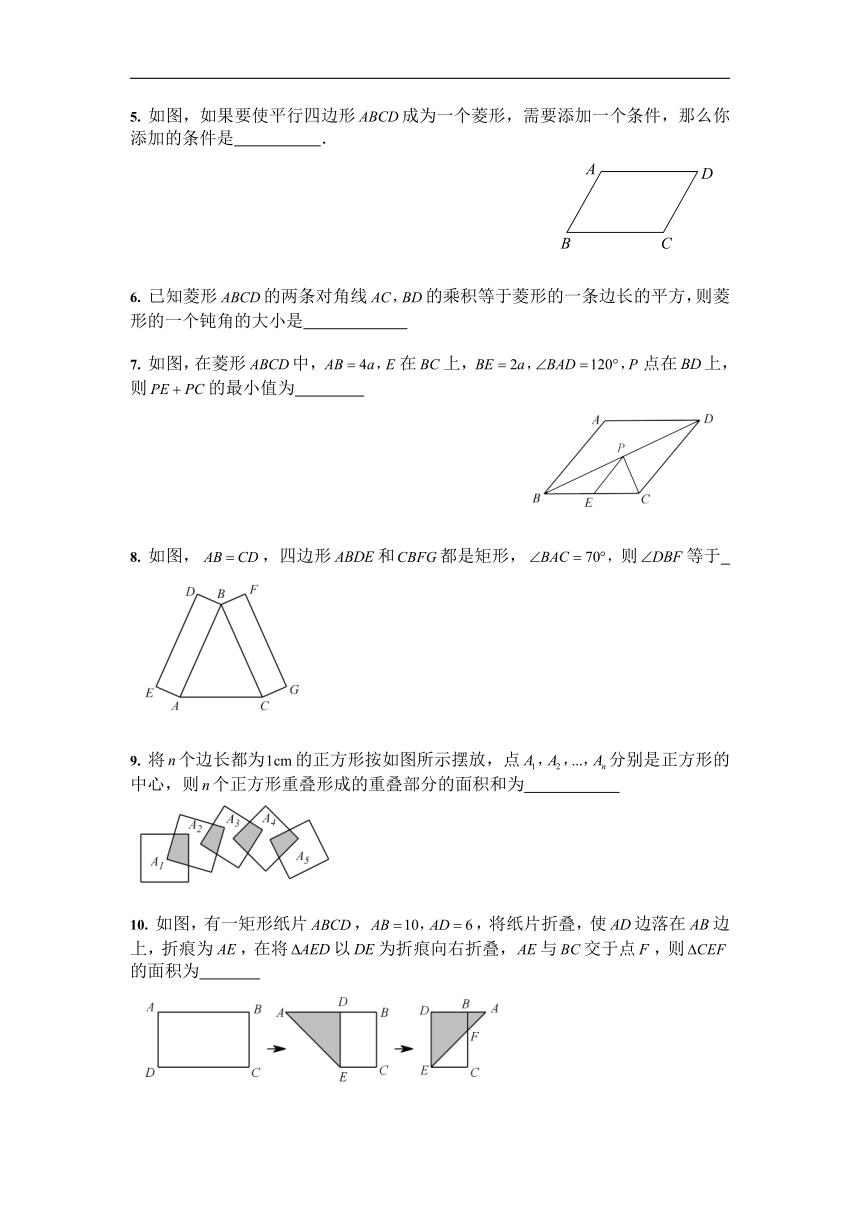
1.
四边形中,、分别是、上的点,、分别是、的中点,当点在上从向移动而点不动时,那么下列结论成立的是
(
)
A.线段的长逐渐增大
B.线段的长逐渐减小
C.线段的长不变
D.线段的长与点的位置有关
2.
如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.
7
B.
9
C.
10
D.
11
3.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
4.
如图,在矩形中,的交点在上,图中面积相等的四边形有(
)
A.对
B.对
C.对
D.对
二、填空题(本大题共6道小题)
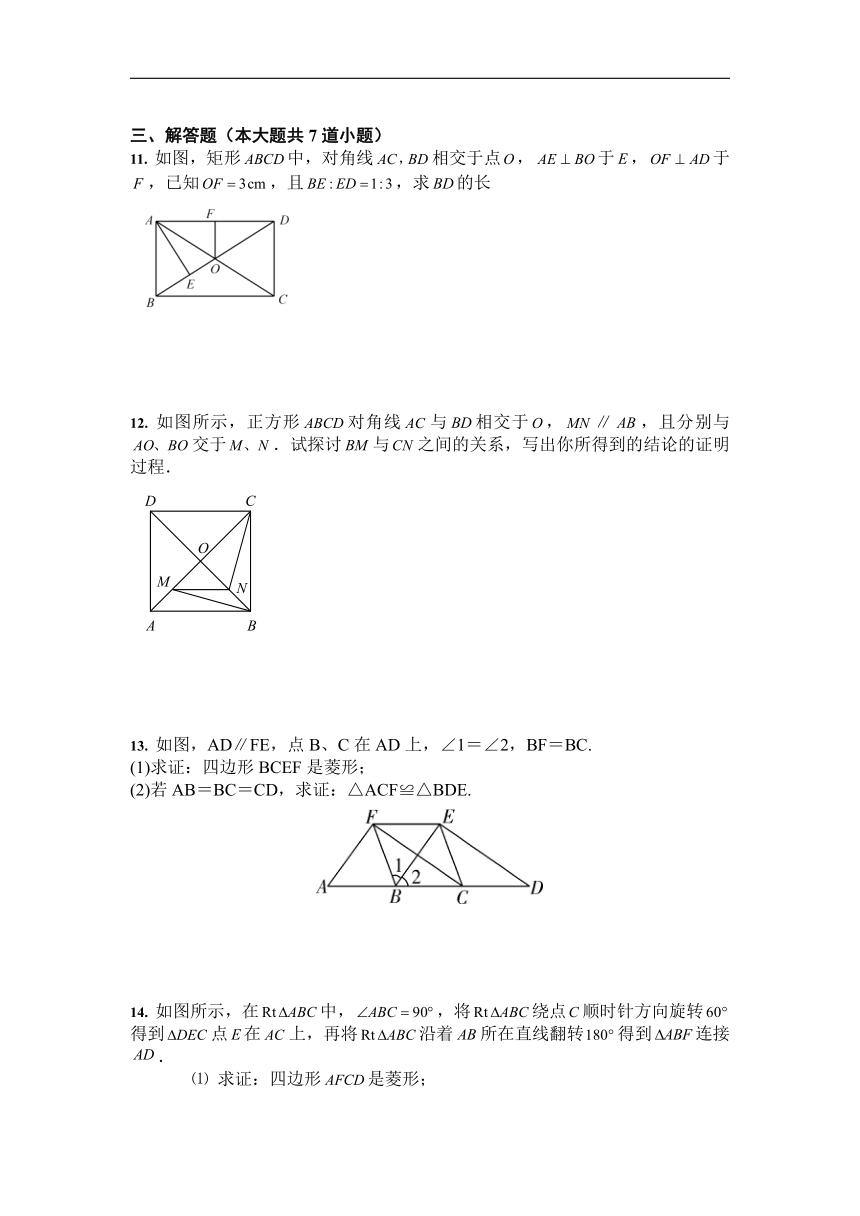
5.
如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是
.
6.
已知菱形的两条对角线的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是
7.
如图,在菱形中,在上,点在上,则的最小值为
8.
如图,,四边形和都是矩形,则等于
9.
将个边长都为的正方形按如图所示摆放,点分别是正方形的中心,则个正方形重叠形成的重叠部分的面积和为
10.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
三、解答题(本大题共7道小题)
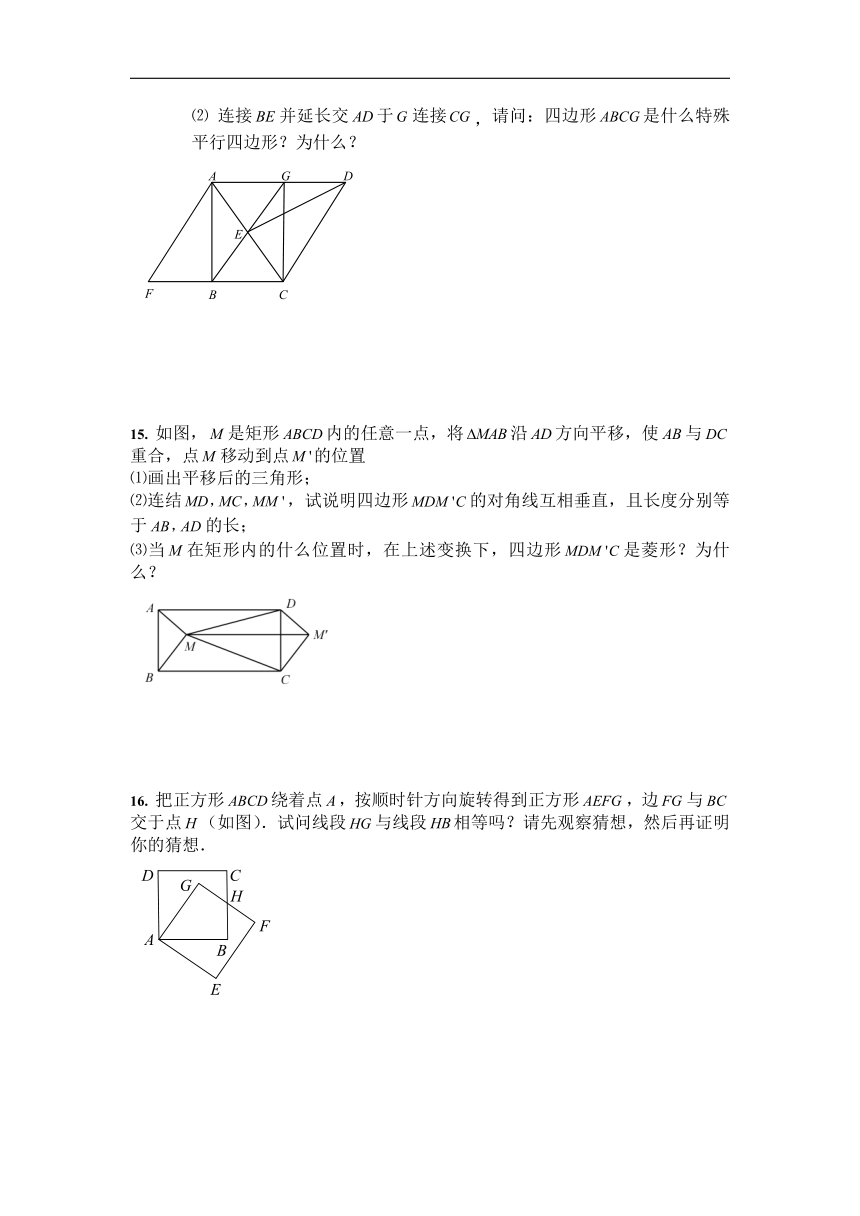
11.
如图,矩形中,对角线相交于点,于,于,已知,且,求的长
12.
如图所示,正方形对角线与相交于,∥,且分别与交于.试探讨与之间的关系,写出你所得到的结论的证明过程.
13.
如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
14.
如图所示,在中,,将绕点顺时针方向旋转得到点在上,再将沿着所在直线翻转得到连接.
⑴
求证:四边形是菱形;
⑵
连接并延长交于连接,请问:四边形是什么特殊平行四边形?为什么?
15.
如图,是矩形内的任意一点,将沿方向平移,使与重合,点移动到点的位置
⑴画出平移后的三角形;
⑵连结,试说明四边形的对角线互相垂直,且长度分别等于的长;
⑶当在矩形内的什么位置时,在上述变换下,四边形是菱形?为什么?
16.
把正方形绕着点,按顺时针方向旋转得到正方形,边与交于点(如图).试问线段与线段相等吗?请先观察猜想,然后再证明你的猜想.
17.
如图,在中,都是等边三角形,求四边形的面积
人教版
八年级下册
第18章
平行四边形
培优训练-答案
一、选择题(本大题共4道小题)
1.
【答案】C
【解析】连结,利用三角形的中位线可得与点无关.
2.
【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长
.
解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
3.
【答案】B
4.
【答案】D
二、填空题(本大题共6道小题)
5.
【答案】
6.
【答案】
【解析】如图,过点作于,则,又,得,
7.
【答案】
【解析】关于对称,连交于,且
为最小值
8.
【答案】
9.
【答案】
10.
【答案】
【解析】,所以可得面积为
三、解答题(本大题共7道小题)
11.
【答案】
【解析】因为,且矩形中,所以,因为,所以
,是等边三角形,即,由条件易得是的中位线,,所以
12.
【答案】
与的关系是:且
∵是正方形,∴
∵∥,∴,∴
∵,
∴≌,∴,
∵,∴
∴
13.
【答案】
证明:(1)∵AD∥EF,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴BF=EF.∵BF=BC,
∴BC=EF.∴四边形BCEF是平行四边形.
∵BF=BC.∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥FE.
∴四边形ABEF、四边形CDEF均为平行四边形,
∴AF=BE,FC=ED.
又∵AC=2BC=BD.∴△ACF≌△BDE.
14.
【答案】
⑴
是由绕点旋转得到
∴,
∴是等边三角形
∴
又∵是由沿所在
直线翻转得到
∴,
∴
∴点、、三点共线
∴是等边三角形
∴
∴
∴四边形是菱形.
⑵
四边形是矩形.
由⑴可知:是等边三角形,于
∴,又∵
∴,
∴,∴
∴四边形是平行四边形,而
∴四边形是矩形.
15.
【答案】
⑴如图,就是所要作的三角形
⑵因为平移到,所以且,四边形是平行四边形,所以,矩形中,,所以,又因为,,所以四边形的对角线互相垂直,且长度分别等于的长
⑶当点是的交点时,四边形是菱形,理由:如图,矩形中,,又因为,可得,所以
四边形是菱形
16.
【答案】
.
证法1:连结,如图.
∵四边形,都是正方形,
∴.
由题意知,
又∵.
∴≌.
∴.
证法2:连结,如图.
∵四边形都是正方形,
∴.
由题意知.
∴.
∴.
∴.
17.
【答案】
由,得,故四边形为平行四边形,又,到的距离为,所以可知:
八年级下册
第18章
平行四边形
培优训练(含答案)
一、选择题(本大题共4道小题)
1.
四边形中,、分别是、上的点,、分别是、的中点,当点在上从向移动而点不动时,那么下列结论成立的是
(
)
A.线段的长逐渐增大
B.线段的长逐渐减小
C.线段的长不变
D.线段的长与点的位置有关
2.
如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.
7
B.
9
C.
10
D.
11
3.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
4.
如图,在矩形中,的交点在上,图中面积相等的四边形有(
)
A.对
B.对
C.对
D.对
二、填空题(本大题共6道小题)
5.
如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是
.
6.
已知菱形的两条对角线的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是
7.
如图,在菱形中,在上,点在上,则的最小值为
8.
如图,,四边形和都是矩形,则等于
9.
将个边长都为的正方形按如图所示摆放,点分别是正方形的中心,则个正方形重叠形成的重叠部分的面积和为
10.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
三、解答题(本大题共7道小题)
11.
如图,矩形中,对角线相交于点,于,于,已知,且,求的长
12.
如图所示,正方形对角线与相交于,∥,且分别与交于.试探讨与之间的关系,写出你所得到的结论的证明过程.
13.
如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
14.
如图所示,在中,,将绕点顺时针方向旋转得到点在上,再将沿着所在直线翻转得到连接.
⑴
求证:四边形是菱形;
⑵
连接并延长交于连接,请问:四边形是什么特殊平行四边形?为什么?
15.
如图,是矩形内的任意一点,将沿方向平移,使与重合,点移动到点的位置
⑴画出平移后的三角形;
⑵连结,试说明四边形的对角线互相垂直,且长度分别等于的长;
⑶当在矩形内的什么位置时,在上述变换下,四边形是菱形?为什么?
16.
把正方形绕着点,按顺时针方向旋转得到正方形,边与交于点(如图).试问线段与线段相等吗?请先观察猜想,然后再证明你的猜想.
17.
如图,在中,都是等边三角形,求四边形的面积
人教版
八年级下册
第18章
平行四边形
培优训练-答案
一、选择题(本大题共4道小题)
1.
【答案】C
【解析】连结,利用三角形的中位线可得与点无关.
2.
【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长
.
解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
3.
【答案】B
4.
【答案】D
二、填空题(本大题共6道小题)
5.
【答案】
6.
【答案】
【解析】如图,过点作于,则,又,得,
7.
【答案】
【解析】关于对称,连交于,且
为最小值
8.
【答案】
9.
【答案】
10.
【答案】
【解析】,所以可得面积为
三、解答题(本大题共7道小题)
11.
【答案】
【解析】因为,且矩形中,所以,因为,所以
,是等边三角形,即,由条件易得是的中位线,,所以
12.
【答案】
与的关系是:且
∵是正方形,∴
∵∥,∴,∴
∵,
∴≌,∴,
∵,∴
∴
13.
【答案】
证明:(1)∵AD∥EF,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴BF=EF.∵BF=BC,
∴BC=EF.∴四边形BCEF是平行四边形.
∵BF=BC.∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥FE.
∴四边形ABEF、四边形CDEF均为平行四边形,
∴AF=BE,FC=ED.
又∵AC=2BC=BD.∴△ACF≌△BDE.
14.
【答案】
⑴
是由绕点旋转得到
∴,
∴是等边三角形
∴
又∵是由沿所在
直线翻转得到
∴,
∴
∴点、、三点共线
∴是等边三角形
∴
∴
∴四边形是菱形.
⑵
四边形是矩形.
由⑴可知:是等边三角形,于
∴,又∵
∴,
∴,∴
∴四边形是平行四边形,而
∴四边形是矩形.
15.
【答案】
⑴如图,就是所要作的三角形
⑵因为平移到,所以且,四边形是平行四边形,所以,矩形中,,所以,又因为,,所以四边形的对角线互相垂直,且长度分别等于的长
⑶当点是的交点时,四边形是菱形,理由:如图,矩形中,,又因为,可得,所以
四边形是菱形
16.
【答案】
.
证法1:连结,如图.
∵四边形,都是正方形,
∴.
由题意知,
又∵.
∴≌.
∴.
证法2:连结,如图.
∵四边形都是正方形,
∴.
由题意知.
∴.
∴.
∴.
17.
【答案】
由,得,故四边形为平行四边形,又,到的距离为,所以可知:
