冀教版数学四年级上册第6单元认识更大的数用计算器探索规律课件(22张PPT)
文档属性
| 名称 | 冀教版数学四年级上册第6单元认识更大的数用计算器探索规律课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 776.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 22:28:22 | ||
图片预览







文档简介
(共22张PPT)
认识更大的数
第2课时
用计算器探索规律
冀教版
数学
四年级
上册
1.经历用计算器计算、探索并发现特殊数学运算规律的过程。
2.会用计算器探索并发现一些特殊运算的规律,能进行有条理的思考和归纳推理。
3.感受数学知识的奥秘,激发用计算器探索数学规律的兴趣和愿望。
按下图给出的顺序计算。
任取一个两位数
如48,是双数,除以2,得24;再除以2,得12;再除以2,得6;再除以2,得3;是单数,乘3再加1,得10;是双数,除以2,得5;是单数,乘3再加1,得16;是双数,除以2,得8;再除以2,得4;再除以2,得2;再除以2,得1。
是双数,除以2;
是单数,乘3再加1
得出结果后,
如上反复进行
最后得出结果1,停止
任取一个三位数,按上面的程序再计算一下,看结果如何。
任选一个自然数,按“逢双数除以2,逢单数乘3再加1”
的规则重复进行运算,最终结果必定是1。这是著名的“角谷猜想”。
如102,是双数,除以2,得51;是单数,乘3再加1,得154;是双数,除以2,得77;是单数,乘3再加1,得232;是双数,除以2,得116;再除以2,得58;再除以2,得29;是单数,乘3再加1,得88……再除以2,得4;再除以2,得2;再除以2,得1。
计算结果还是1。
将角谷猜想中的“逢单数乘3再加1”,改为“逢单数乘5再加1”,结果会怎样??
自己可以大胆作个猜想!
将“角谷猜想”中的“逢单数乘3再加1”,改为“逢单数乘5再加1”
,结果不等于1,没有规律。
如34,是双数,除以2,得17;是单数,乘5再加1,得86;是双数,除以2,得43;是单数,乘5再加1,得216;是双数,除以2,得108;再除以2,得54;再除以2,得27;是单数,乘5再加1,得136;是双数,除以2,得68,再除以2,得34……
哥德巴赫猜想
1742年,德国数学家哥德巴赫提出了这样的猜想:任何大于2的偶数,都可以用两个质数的和表示。如,4=2+2,6=3+3,8=3+5,14=3+11=7+7等。人们对大于4、小于330000000的偶数进行了检验,结果表明这个猜想是正确的。
但是,
这个猜想对于大于2的任意偶数都正确吗?这需要得到科学的证明。二百多年来,众多的数学家为证明这一猜想付出了艰辛的劳动,1966年,
我国数学家陈景润在这一猜想证明方面取得了举世嘱目的成果。
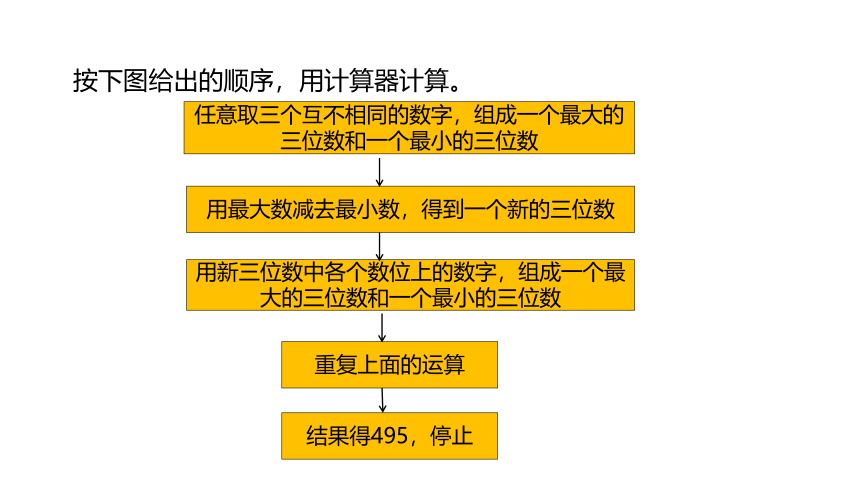
按下图给出的顺序,用计算器计算。
任意取三个互不相同的数字,组成一个最大的三位数和一个最小的三位数
用最大数减去最小数,得到一个新的三位数
用新三位数中各个数位上的数字,组成一个最大的三位数和一个最小的三位数
重复上面的运算
结果得495,停止
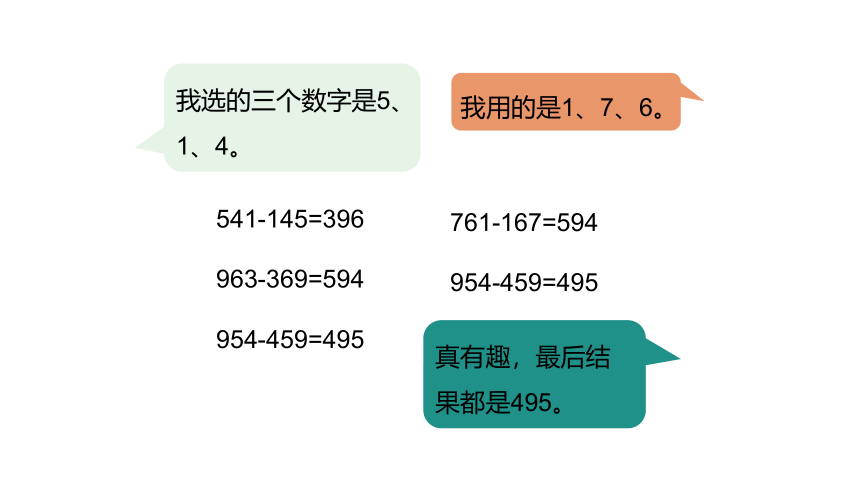
541-145=396
963-369=594
954-459=495
761-167=594
954-459=495
我选的三个数字是5、1、4。
真有趣,最后结果都是495。
我用的是1、7、6。
任意选四个互不相同的数字,组成一个最大的四位数和一个最小的四位数。
1
例如选数字1,3,5,7,组成的最大的四位数是7531,组成的最小的四位数是1357。7531-1357=6174??
同理,
7641-1467=?6174
发现:按照题意重复运算的最终结果都为6174。
用第8页的规则进行探索,你发现了什么?
225
积的规律是:积的十位和个位数是5乘5的积“25”;积的百位和千位数是乘数“十位上的数字加1”再乘自己。例如“35
×
35”
,5×5=25,
(3+1)
×3=12,所以“35
×
35=
1225”
。
15×15=
35×35=
55×55=
25×25=
45×45=
65×65=
625
1225
2025
3025
4225
2
用计算器计算下面各题,看一看积有什么规律。
角谷猜想:任选一个自然数,按“逢双数除以2,逢单数乘3再加1”
的规则重复进行运算,最终结果必定是1。
用计算器计算。
6870-
687-
687-
687=
809+34+56+78=
267×67=
349×34=
9095÷85=
28944÷72=
56×108=
16324÷28=
4809
977
17889
11866
107
402
6048
583
1
有趣的算式。
1=1×1
1+3=4=2×2
1+3+5=9=3×3
1+3+5+7=16=4×4
……
从1开始的连续奇数项相加,和等于项数的平方。
(1)从这些算式中寻找规律。
2
正确。
(2)用计算器来验证规律是否正确。
(3)按规律写出两组算式。
1+3+5+7+9+11+13+15=64=8×8
1+3+5+7+9+11+13+15+17=81=9×9
1+3+5+7+9=25=5×5
1+3+5+7+9+11=36=6×6
1+3+5+7+9+11+13=49=7×7
2
先计算,再根据规律填空。
8547×13=
8547×26=
8547×39=
8547×
(
)
=
444444
8547×
(
)
=
555555
8547×
(
)
=
888888
111111
222222
333333
52
65
104
3
1×8+1=
12×8+2=
123×8+3=
1234×8+4=
123456×8+6=
123456789×8+9=
9
98
987
9876
987654
987654321
4
先用计算器算出每组前三道算式的得数,再根据规律直接写出其余算式的得数。
(1)
(2)
108÷9=
1107÷9=
11106÷9=
111105÷9=?
1111104÷9=
11111103÷9=
12
123
1234
12345
123456
1234567
4
先用计算器算出每组前三道算式的得数。再根据规律直接写出其余算式的得数。
3÷7=
(
)
4÷7=
(
)
5÷7=
(
)
1÷7=0.142857
2÷7=0.285714
0.428571
0.
571428
0.
714285
5
根据规律直接写出答案。
1÷11=
0.0909……
2÷11=
0.1818……
3÷11=
0.2727
……
4÷11=_____________
5÷11=_____________
6÷11=_____________
0.3636……
0.4545……
0.5454……
6
用计算器算出前三道算式,然后根据规律写出其他算式的得数。
111111÷37037=3
222222÷37037=6
(
)÷37037=9
(
)÷37037=12
555555÷37037=(
)
666666÷37037=(
)
777777÷37037=(
)
333333
444444
15
18
21
7
根据你的发现,把其他算式补充完整。
111111111÷9=____________
222222222÷18=____________
333333333÷27=____________
444444444÷36=____________
666666666÷54=____________
888888888÷72=____________
12345679
12345679
12345679
12345679
12345679
12345679
8
用计算器计算前两道题的结果,然后试着直接写出后四道题的商。
99×99=9801
999×999=998001
9999×9999=99980001
99999×99999=______________
999999×999999=______________
9999800001
999998000001
9
根据你发现的规律,直接写得数。
认识更大的数
第2课时
用计算器探索规律
冀教版
数学
四年级
上册
1.经历用计算器计算、探索并发现特殊数学运算规律的过程。
2.会用计算器探索并发现一些特殊运算的规律,能进行有条理的思考和归纳推理。
3.感受数学知识的奥秘,激发用计算器探索数学规律的兴趣和愿望。
按下图给出的顺序计算。
任取一个两位数
如48,是双数,除以2,得24;再除以2,得12;再除以2,得6;再除以2,得3;是单数,乘3再加1,得10;是双数,除以2,得5;是单数,乘3再加1,得16;是双数,除以2,得8;再除以2,得4;再除以2,得2;再除以2,得1。
是双数,除以2;
是单数,乘3再加1
得出结果后,
如上反复进行
最后得出结果1,停止
任取一个三位数,按上面的程序再计算一下,看结果如何。
任选一个自然数,按“逢双数除以2,逢单数乘3再加1”
的规则重复进行运算,最终结果必定是1。这是著名的“角谷猜想”。
如102,是双数,除以2,得51;是单数,乘3再加1,得154;是双数,除以2,得77;是单数,乘3再加1,得232;是双数,除以2,得116;再除以2,得58;再除以2,得29;是单数,乘3再加1,得88……再除以2,得4;再除以2,得2;再除以2,得1。
计算结果还是1。
将角谷猜想中的“逢单数乘3再加1”,改为“逢单数乘5再加1”,结果会怎样??
自己可以大胆作个猜想!
将“角谷猜想”中的“逢单数乘3再加1”,改为“逢单数乘5再加1”
,结果不等于1,没有规律。
如34,是双数,除以2,得17;是单数,乘5再加1,得86;是双数,除以2,得43;是单数,乘5再加1,得216;是双数,除以2,得108;再除以2,得54;再除以2,得27;是单数,乘5再加1,得136;是双数,除以2,得68,再除以2,得34……
哥德巴赫猜想
1742年,德国数学家哥德巴赫提出了这样的猜想:任何大于2的偶数,都可以用两个质数的和表示。如,4=2+2,6=3+3,8=3+5,14=3+11=7+7等。人们对大于4、小于330000000的偶数进行了检验,结果表明这个猜想是正确的。
但是,
这个猜想对于大于2的任意偶数都正确吗?这需要得到科学的证明。二百多年来,众多的数学家为证明这一猜想付出了艰辛的劳动,1966年,
我国数学家陈景润在这一猜想证明方面取得了举世嘱目的成果。
按下图给出的顺序,用计算器计算。
任意取三个互不相同的数字,组成一个最大的三位数和一个最小的三位数
用最大数减去最小数,得到一个新的三位数
用新三位数中各个数位上的数字,组成一个最大的三位数和一个最小的三位数
重复上面的运算
结果得495,停止
541-145=396
963-369=594
954-459=495
761-167=594
954-459=495
我选的三个数字是5、1、4。
真有趣,最后结果都是495。
我用的是1、7、6。
任意选四个互不相同的数字,组成一个最大的四位数和一个最小的四位数。
1
例如选数字1,3,5,7,组成的最大的四位数是7531,组成的最小的四位数是1357。7531-1357=6174??
同理,
7641-1467=?6174
发现:按照题意重复运算的最终结果都为6174。
用第8页的规则进行探索,你发现了什么?
225
积的规律是:积的十位和个位数是5乘5的积“25”;积的百位和千位数是乘数“十位上的数字加1”再乘自己。例如“35
×
35”
,5×5=25,
(3+1)
×3=12,所以“35
×
35=
1225”
。
15×15=
35×35=
55×55=
25×25=
45×45=
65×65=
625
1225
2025
3025
4225
2
用计算器计算下面各题,看一看积有什么规律。
角谷猜想:任选一个自然数,按“逢双数除以2,逢单数乘3再加1”
的规则重复进行运算,最终结果必定是1。
用计算器计算。
6870-
687-
687-
687=
809+34+56+78=
267×67=
349×34=
9095÷85=
28944÷72=
56×108=
16324÷28=
4809
977
17889
11866
107
402
6048
583
1
有趣的算式。
1=1×1
1+3=4=2×2
1+3+5=9=3×3
1+3+5+7=16=4×4
……
从1开始的连续奇数项相加,和等于项数的平方。
(1)从这些算式中寻找规律。
2
正确。
(2)用计算器来验证规律是否正确。
(3)按规律写出两组算式。
1+3+5+7+9+11+13+15=64=8×8
1+3+5+7+9+11+13+15+17=81=9×9
1+3+5+7+9=25=5×5
1+3+5+7+9+11=36=6×6
1+3+5+7+9+11+13=49=7×7
2
先计算,再根据规律填空。
8547×13=
8547×26=
8547×39=
8547×
(
)
=
444444
8547×
(
)
=
555555
8547×
(
)
=
888888
111111
222222
333333
52
65
104
3
1×8+1=
12×8+2=
123×8+3=
1234×8+4=
123456×8+6=
123456789×8+9=
9
98
987
9876
987654
987654321
4
先用计算器算出每组前三道算式的得数,再根据规律直接写出其余算式的得数。
(1)
(2)
108÷9=
1107÷9=
11106÷9=
111105÷9=?
1111104÷9=
11111103÷9=
12
123
1234
12345
123456
1234567
4
先用计算器算出每组前三道算式的得数。再根据规律直接写出其余算式的得数。
3÷7=
(
)
4÷7=
(
)
5÷7=
(
)
1÷7=0.142857
2÷7=0.285714
0.428571
0.
571428
0.
714285
5
根据规律直接写出答案。
1÷11=
0.0909……
2÷11=
0.1818……
3÷11=
0.2727
……
4÷11=_____________
5÷11=_____________
6÷11=_____________
0.3636……
0.4545……
0.5454……
6
用计算器算出前三道算式,然后根据规律写出其他算式的得数。
111111÷37037=3
222222÷37037=6
(
)÷37037=9
(
)÷37037=12
555555÷37037=(
)
666666÷37037=(
)
777777÷37037=(
)
333333
444444
15
18
21
7
根据你的发现,把其他算式补充完整。
111111111÷9=____________
222222222÷18=____________
333333333÷27=____________
444444444÷36=____________
666666666÷54=____________
888888888÷72=____________
12345679
12345679
12345679
12345679
12345679
12345679
8
用计算器计算前两道题的结果,然后试着直接写出后四道题的商。
99×99=9801
999×999=998001
9999×9999=99980001
99999×99999=______________
999999×999999=______________
9999800001
999998000001
9
根据你发现的规律,直接写得数。
