沪科版八年级下册第18章 勾股定理期末复习自测试卷(无答案)
文档属性
| 名称 | 沪科版八年级下册第18章 勾股定理期末复习自测试卷(无答案) | 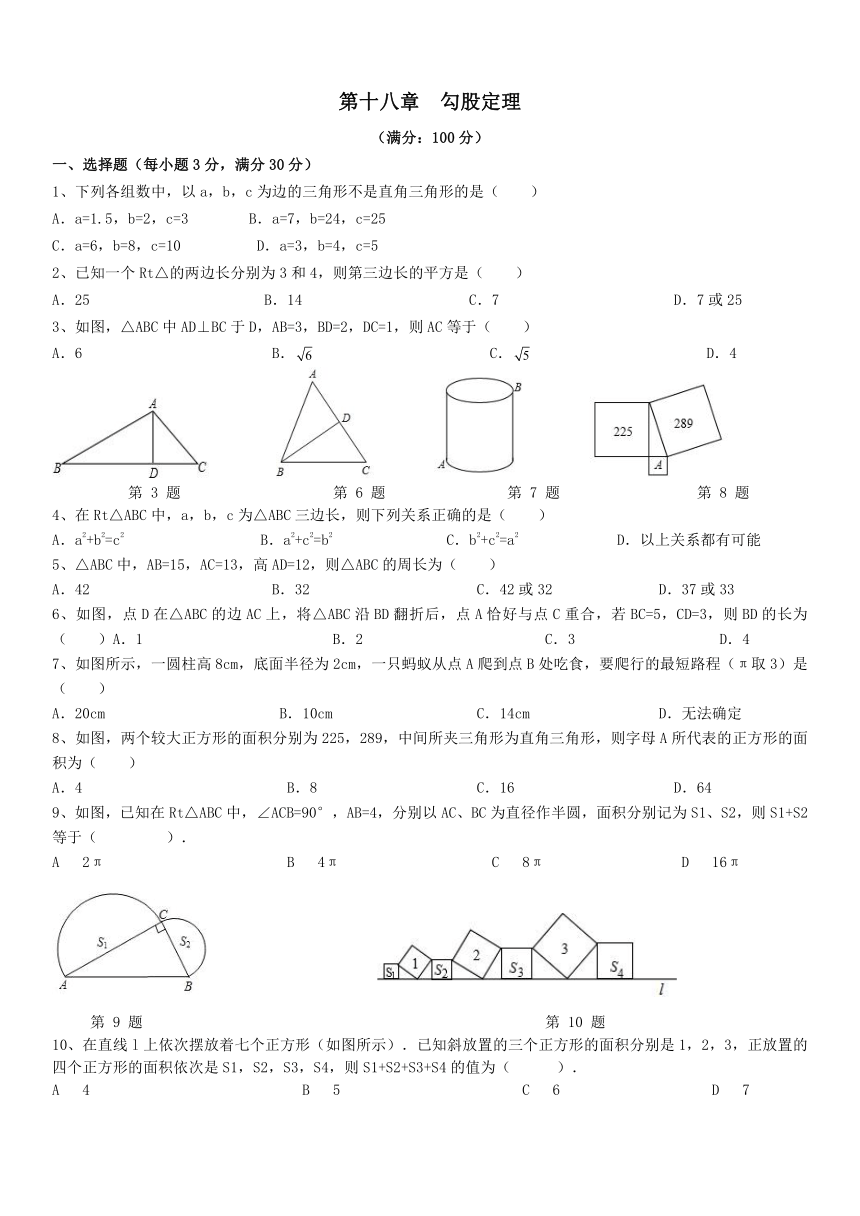 | |
| 格式 | zip | ||
| 文件大小 | 126.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 08:16:44 | ||
图片预览


文档简介
第十八章
勾股定理
(满分:100分)
一、选择题(每小题3分,满分30分)
1、下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3
B.a=7,b=24,c=25
C.a=6,b=8,c=10
D.a=3,b=4,c=5
2、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A.25
B.14
C.7
D.7或25
3、如图,△ABC中AD⊥BC于D,AB=3,BD=2,DC=1,则AC等于( )
A.6
B.
C.
D.4
第
3
题
第
6
题
第
7
题
第
8
题
4、在Rt△ABC中,a,b,c为△ABC三边长,则下列关系正确的是( )
A.a2+b2=c2
B.a2+c2=b2
C.b2+c2=a2
D.以上关系都有可能
5、△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42或32
D.37或33
6、如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合,若BC=5,CD=3,则BD的长为( )A.1
B.2
C.3
D.4
7、如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.20cm
B.10cm
C.14cm
D.无法确定
8、如图,两个较大正方形的面积分别为225,289,中间所夹三角形为直角三角形,则字母A所代表的正方形的面积为( )
A.4
B.8
C.16
D.64
9、如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于(
).
A
2π
B
4π
C
8π
D
16π
第
9
题
第
10
题
10、在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4的值为(
).
A
4
B
5
C
6
D
7
二、填空题(每小题4分,满分20分)
11、已知a,b,c分别是Rt△ABC的两条直角边长和斜边长,且a+b=14,c=10,则S△ABC=
.
12、在直角三角形中,若两直角边的长分别为1cm,2cm,则斜边长的高为
cm.
13、如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有
米
第
13
题
第
14
题
第
15
题
14、有一只小鸟在一棵高4m的小树梢上捉虫子,它的伙伴在离该树12m,高20m的一棵大树的树梢上发出友好的叫声,它立刻以4m/s的速度飞向大树树梢,那么这只小鸟至少
秒才可能到达大树和伙伴在一起?
15、课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为
20013
cm.
三、解答题(满分50分)
16、若a,b,c是△ABC的三边长,且a,b,c满足(a-5)2+(b-12)2+|c-13|=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
17、如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?
18、如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.
19、如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
20、【阅读资料】小学学过图形中的长方形有一下两个性质:(1)四个角是直角;(2)对边相等;
根据资料解决问题:如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.
21、如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
勾股定理
(满分:100分)
一、选择题(每小题3分,满分30分)
1、下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3
B.a=7,b=24,c=25
C.a=6,b=8,c=10
D.a=3,b=4,c=5
2、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A.25
B.14
C.7
D.7或25
3、如图,△ABC中AD⊥BC于D,AB=3,BD=2,DC=1,则AC等于( )
A.6
B.
C.
D.4
第
3
题
第
6
题
第
7
题
第
8
题
4、在Rt△ABC中,a,b,c为△ABC三边长,则下列关系正确的是( )
A.a2+b2=c2
B.a2+c2=b2
C.b2+c2=a2
D.以上关系都有可能
5、△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42或32
D.37或33
6、如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合,若BC=5,CD=3,则BD的长为( )A.1
B.2
C.3
D.4
7、如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.20cm
B.10cm
C.14cm
D.无法确定
8、如图,两个较大正方形的面积分别为225,289,中间所夹三角形为直角三角形,则字母A所代表的正方形的面积为( )
A.4
B.8
C.16
D.64
9、如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于(
).
A
2π
B
4π
C
8π
D
16π
第
9
题
第
10
题
10、在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4的值为(
).
A
4
B
5
C
6
D
7
二、填空题(每小题4分,满分20分)
11、已知a,b,c分别是Rt△ABC的两条直角边长和斜边长,且a+b=14,c=10,则S△ABC=
.
12、在直角三角形中,若两直角边的长分别为1cm,2cm,则斜边长的高为
cm.
13、如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有
米
第
13
题
第
14
题
第
15
题
14、有一只小鸟在一棵高4m的小树梢上捉虫子,它的伙伴在离该树12m,高20m的一棵大树的树梢上发出友好的叫声,它立刻以4m/s的速度飞向大树树梢,那么这只小鸟至少
秒才可能到达大树和伙伴在一起?
15、课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为
20013
cm.
三、解答题(满分50分)
16、若a,b,c是△ABC的三边长,且a,b,c满足(a-5)2+(b-12)2+|c-13|=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
17、如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?
18、如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.
19、如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
20、【阅读资料】小学学过图形中的长方形有一下两个性质:(1)四个角是直角;(2)对边相等;
根据资料解决问题:如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.
21、如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
