华师大版七年级数学下册课件:10.4中心对称(共24张PPT)
文档属性
| 名称 | 华师大版七年级数学下册课件:10.4中心对称(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-25 11:51:47 | ||
图片预览








文档简介
(共24张PPT)
第10章
轴对称、平移与旋转
10.4
中心对称
什么是轴对称图形?
什么是轴对称?
什么是旋转?
什么是旋转对称图形?
温故知新
创设问题情境
上面图形中哪个图形旋转180°后能与自身重合?
你能举出日常生活中旋转180°后能与自身重合的例子吗?
中心对称图形
一个图形绕着某中心点旋转180°后能与自身重合,我们就把这种图形叫做中心对称图形,这个中心点叫做对称中心.
你能举一些中心对称图形吗?它们的对称中心在哪里?
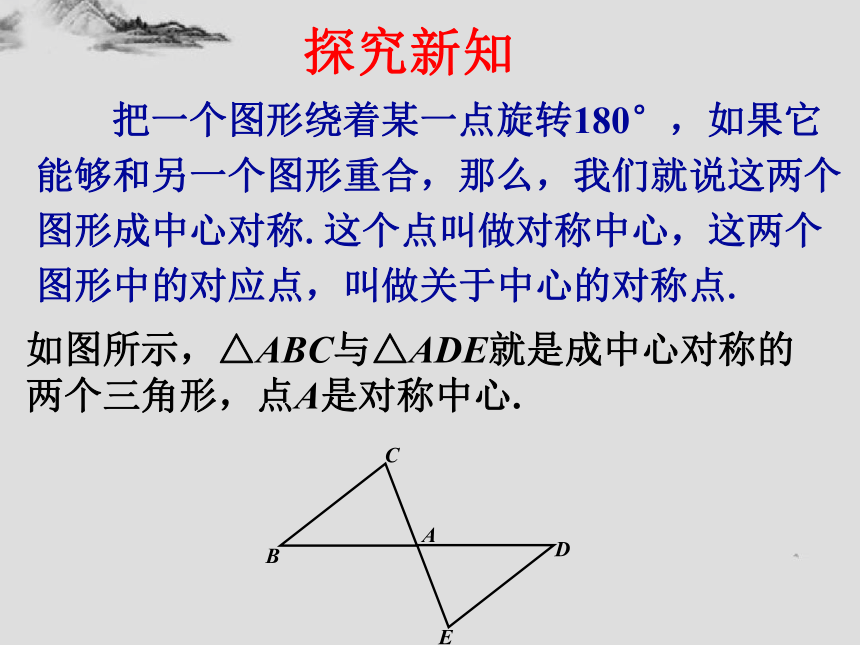
探究新知
把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称.这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
如图所示,△ABC与△ADE就是成中心对称的
两个三角形,点A是对称中心.
OA=OA′,OB=OB′,OC=OC′.
探究新知
在下图中,
△ABC与△A′B′C′关于点O是成中心对称的,除了对应线段相等外,你能从图中找到哪些相等的线段呢?
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
探究新知
在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
【归纳】
关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
反过来,如果两个图形的所有对应点连线都经过某一点,并且被这点平分,那么这两个图形关于这一点对称.
中心对称的多边形很多,如边数为偶数的正多边形都是中心对称图形。
3.中心对称与轴对称的联系与区别
F
D
E
探究新知
例1
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
解:(1)连接AO并延长AO到点D,使OD=OA,于是得到点A的对应点D;
(2)同样画出点B和点C关于点O的对称点E和点F;
(3)顺次连接DE、EF、FD.△DEF为所求的三角形.
探究新知
●
1.下列图形中,是中心对称图形的是(
)
随堂演练
A
2.下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
A
ABCDEMTUVWY
HIOX
HINO
SXZ
HINO
SXZ
3.仔细观察下图所列的26个英文字母,将相应的
字母填入表中适当的空格内.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
对称形式
轴对称
旋转对称
中心对称
只有一条对称轴
有两条对称轴
英文字母
4.如图,已知四边形ABCD和点O,画出四边形
A′B′C′D′,使四边形A′B′C′D′和四边形ABCD
关于点O成中心对称.
5.如图,已知△ABC和过点O的两条互相垂直的直线x、
y,画出△ABC关于直线x对称的△A′B′C′,再画出
△A′B′C′关于直线y对称的△A′′
B′′
C′′,
△A′′
B′′
C′′
与△ABC是否关于点O成中心对称?
△A′′
B′′
C′′与△ABC关于点O成中心对称.
6.
如图1,先在纸上画△ABC、点P,
再画△ABC关于点P成中心对称的△A′B′C′.
如图2,在图1的基础上,过点P任意画一条直线,画出△ABC关于此直线对称的△A′′
B′′
C′′.
观察△A′B′C′和△A′′
B′′
C′′,你发现了什么?
△ABC与△A′′
B′′
C′′关于此直线过点P的垂线对称.
7.按下列要求正确画出图形:
(1)已知△ABC和直线MN,画出△ABC关于直线MN对称的图形;
(2)已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
解:(1)过点A作AA′⊥MN且使MN垂直平分AA′,过点B作BB′⊥MN且使MN垂直平分BB′,过点C作CC′⊥MN且使MN垂直平分CC′,然后顺次连接即可;
△A′B′C′如图所示;
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
8.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
1.说说中心对称和中心对称图形的区别和联系.
2.中心对称有什么基本性质?
课堂小结
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
第10章
轴对称、平移与旋转
10.4
中心对称
什么是轴对称图形?
什么是轴对称?
什么是旋转?
什么是旋转对称图形?
温故知新
创设问题情境
上面图形中哪个图形旋转180°后能与自身重合?
你能举出日常生活中旋转180°后能与自身重合的例子吗?
中心对称图形
一个图形绕着某中心点旋转180°后能与自身重合,我们就把这种图形叫做中心对称图形,这个中心点叫做对称中心.
你能举一些中心对称图形吗?它们的对称中心在哪里?
探究新知
把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称.这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
如图所示,△ABC与△ADE就是成中心对称的
两个三角形,点A是对称中心.
OA=OA′,OB=OB′,OC=OC′.
探究新知
在下图中,
△ABC与△A′B′C′关于点O是成中心对称的,除了对应线段相等外,你能从图中找到哪些相等的线段呢?
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
探究新知
在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
【归纳】
关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
反过来,如果两个图形的所有对应点连线都经过某一点,并且被这点平分,那么这两个图形关于这一点对称.
中心对称的多边形很多,如边数为偶数的正多边形都是中心对称图形。
3.中心对称与轴对称的联系与区别
F
D
E
探究新知
例1
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
解:(1)连接AO并延长AO到点D,使OD=OA,于是得到点A的对应点D;
(2)同样画出点B和点C关于点O的对称点E和点F;
(3)顺次连接DE、EF、FD.△DEF为所求的三角形.
探究新知
●
1.下列图形中,是中心对称图形的是(
)
随堂演练
A
2.下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
A
ABCDEMTUVWY
HIOX
HINO
SXZ
HINO
SXZ
3.仔细观察下图所列的26个英文字母,将相应的
字母填入表中适当的空格内.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
对称形式
轴对称
旋转对称
中心对称
只有一条对称轴
有两条对称轴
英文字母
4.如图,已知四边形ABCD和点O,画出四边形
A′B′C′D′,使四边形A′B′C′D′和四边形ABCD
关于点O成中心对称.
5.如图,已知△ABC和过点O的两条互相垂直的直线x、
y,画出△ABC关于直线x对称的△A′B′C′,再画出
△A′B′C′关于直线y对称的△A′′
B′′
C′′,
△A′′
B′′
C′′
与△ABC是否关于点O成中心对称?
△A′′
B′′
C′′与△ABC关于点O成中心对称.
6.
如图1,先在纸上画△ABC、点P,
再画△ABC关于点P成中心对称的△A′B′C′.
如图2,在图1的基础上,过点P任意画一条直线,画出△ABC关于此直线对称的△A′′
B′′
C′′.
观察△A′B′C′和△A′′
B′′
C′′,你发现了什么?
△ABC与△A′′
B′′
C′′关于此直线过点P的垂线对称.
7.按下列要求正确画出图形:
(1)已知△ABC和直线MN,画出△ABC关于直线MN对称的图形;
(2)已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
解:(1)过点A作AA′⊥MN且使MN垂直平分AA′,过点B作BB′⊥MN且使MN垂直平分BB′,过点C作CC′⊥MN且使MN垂直平分CC′,然后顺次连接即可;
△A′B′C′如图所示;
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
8.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
1.说说中心对称和中心对称图形的区别和联系.
2.中心对称有什么基本性质?
课堂小结
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
