人教版六年级数学下册:6.4 数学思考 课件(共17张PPT)
文档属性
| 名称 | 人教版六年级数学下册:6.4 数学思考 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-25 11:42:20 | ||
图片预览


文档简介
(共17张PPT)
人民教育出版社
小学数学六年级下册
数学思考
1
别着急,从2个点开始,逐渐增加点数,找找规律。
8个点可以连成多少条线段?
太乱了,我都数晕了。
一、直接导入,发现问题
点数
增加条数
总条数
2
A
B
1
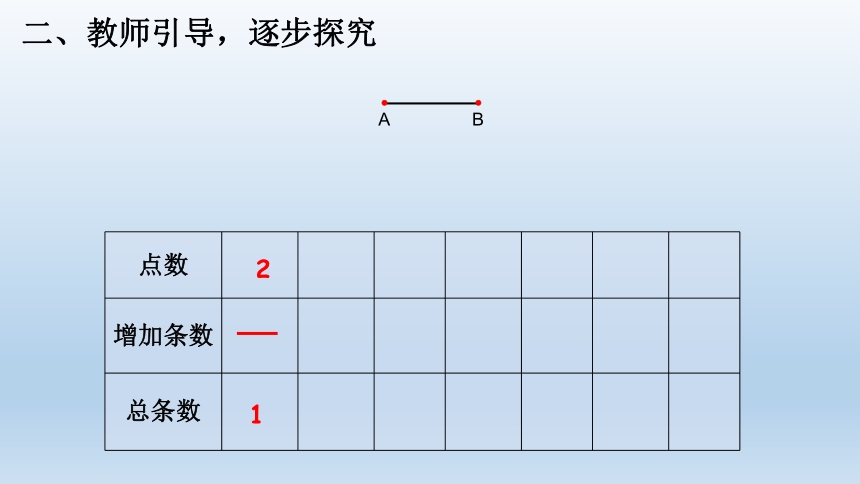
二、教师引导,逐步探究
点数
增加条数
总条数
2
1
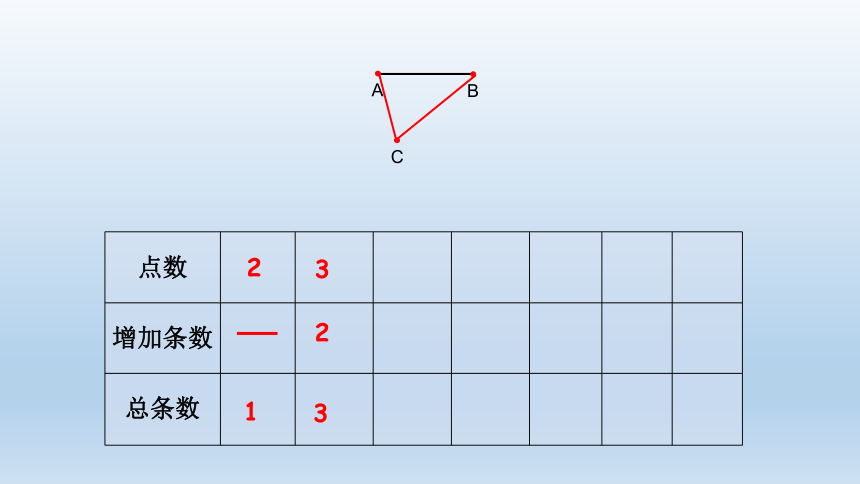
3
C
A
B
3
2
点数
增加条数
总条数
2
1
3
C
A
B
3
2
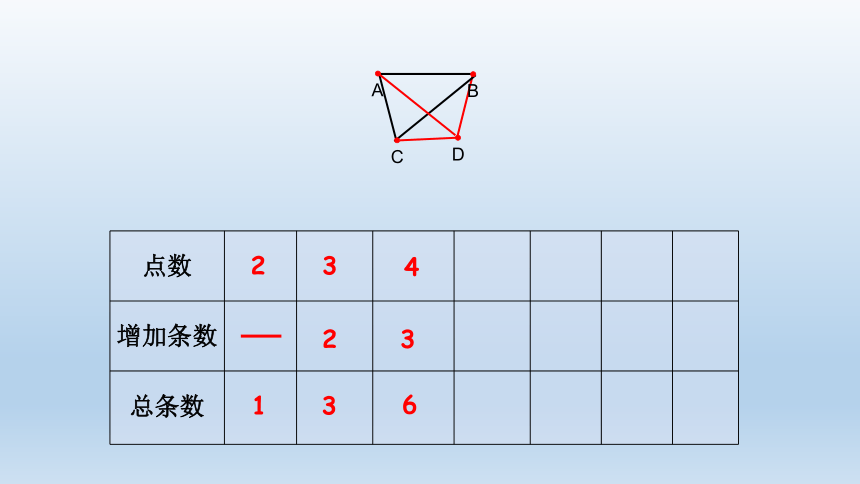
D
4
6
3
点数
增加条数
总条数
2
1
3
C
B
3
2
D
4
6
3
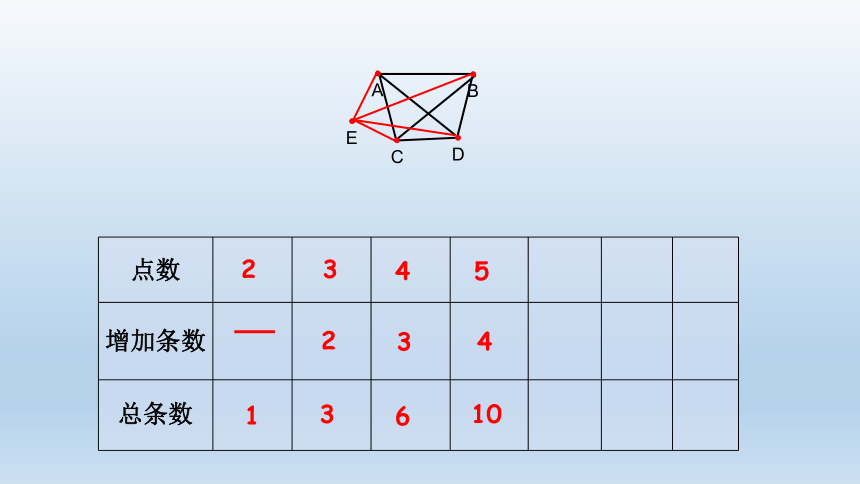
5
E
A
10
4
点数
增加条数
总条数
2
1
3
C
3
2
D
4
6
3
5
10
4
6
A
B
E
F
15
5
点数
增加条数
总条数
2
1
3
3
2
4
6
3
5
10
4
6
A
B
15
5
7
C
D
E
F
G
21
6
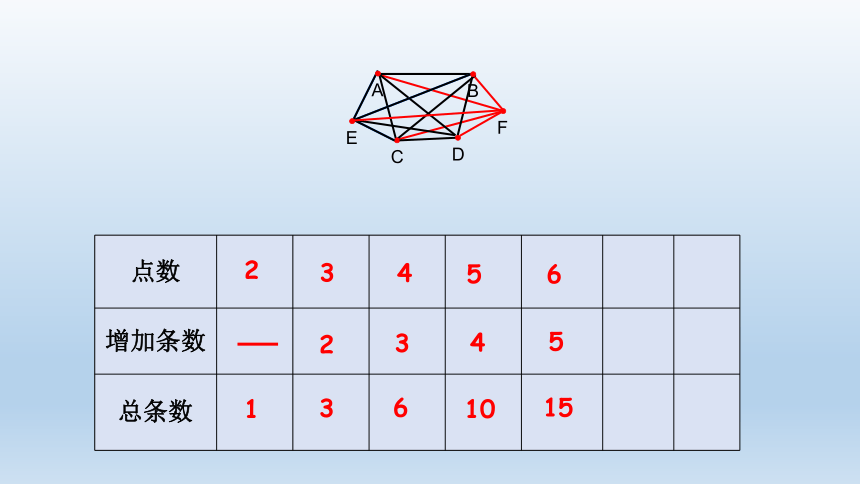
点数
增加条数
总条数
2
1
3
3
2
4
6
3
5
10
4
6
15
5
7
C
D
E
F
G
21
6
8
H
不画出来,你知道增加了几条线段吗?
7
28
B
A
点数
增加条数
总条数
1
3
3
2
4
6
3
5
10
4
6
15
5
7
21
6
8
7
28
2个点连成线段的条数:
1(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4=10(条)
1+2+3+4+5=15(条)
1+2+3+4+5+6=21(条)
1+2+3+4+5+6+7=28(条)
3个点连成线段的条数:
4个点连成线段的条数:
5个点连成线段的条数:
6个点连成线段的条数:
7个点连成线段的条数:
8个点连成线段的条数:
n个点连成线段的条数:
1+2+3+4+……+(n-1)
2
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+17+18+19=190(条)
12个点连成线段的条数:
20个点连成线段的条数:
三、归纳小结,提升思想
观察下图,想一想。(1)第7幅图有多少个棋子?第15幅图呢?
问题:1.
从最简单的数据开始,数一数每幅图各有多少个棋子?
2.在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1
2×2
3×3
4×4
1
4
9
16
四、巩固练习,提升能力
问题:1.
第7幅图每行有几个棋子?有几行?共有几个棋子?
3.
第15幅图共有几个棋子?
7×7=49(个)
15×15=225(个)
想一想:(1)第7幅图有多少个棋子?第15幅图呢?
2.
每边的棋子数与图形的序号有什么关系?
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
想一想:(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n
×
n
=
棋子总数
n2
=棋子总数
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
2、摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(15根)
…
平行四边形
多边形
边数
3
4
5
6
内角和
180°
360°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
多边形内角和=(边数-2)×180°
(9-2)×180°=1260°
问题:遇到复杂的问题,你可以怎样思考?
1.
化繁为简
2.
画图、枚举
3.
有序思考
4.
探究规律
五、回顾所学,课堂总结
人民教育出版社
小学数学六年级下册
数学思考
1
别着急,从2个点开始,逐渐增加点数,找找规律。
8个点可以连成多少条线段?
太乱了,我都数晕了。
一、直接导入,发现问题
点数
增加条数
总条数
2
A
B
1
二、教师引导,逐步探究
点数
增加条数
总条数
2
1
3
C
A
B
3
2
点数
增加条数
总条数
2
1
3
C
A
B
3
2
D
4
6
3
点数
增加条数
总条数
2
1
3
C
B
3
2
D
4
6
3
5
E
A
10
4
点数
增加条数
总条数
2
1
3
C
3
2
D
4
6
3
5
10
4
6
A
B
E
F
15
5
点数
增加条数
总条数
2
1
3
3
2
4
6
3
5
10
4
6
A
B
15
5
7
C
D
E
F
G
21
6
点数
增加条数
总条数
2
1
3
3
2
4
6
3
5
10
4
6
15
5
7
C
D
E
F
G
21
6
8
H
不画出来,你知道增加了几条线段吗?
7
28
B
A
点数
增加条数
总条数
1
3
3
2
4
6
3
5
10
4
6
15
5
7
21
6
8
7
28
2个点连成线段的条数:
1(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4=10(条)
1+2+3+4+5=15(条)
1+2+3+4+5+6=21(条)
1+2+3+4+5+6+7=28(条)
3个点连成线段的条数:
4个点连成线段的条数:
5个点连成线段的条数:
6个点连成线段的条数:
7个点连成线段的条数:
8个点连成线段的条数:
n个点连成线段的条数:
1+2+3+4+……+(n-1)
2
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+17+18+19=190(条)
12个点连成线段的条数:
20个点连成线段的条数:
三、归纳小结,提升思想
观察下图,想一想。(1)第7幅图有多少个棋子?第15幅图呢?
问题:1.
从最简单的数据开始,数一数每幅图各有多少个棋子?
2.在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1
2×2
3×3
4×4
1
4
9
16
四、巩固练习,提升能力
问题:1.
第7幅图每行有几个棋子?有几行?共有几个棋子?
3.
第15幅图共有几个棋子?
7×7=49(个)
15×15=225(个)
想一想:(1)第7幅图有多少个棋子?第15幅图呢?
2.
每边的棋子数与图形的序号有什么关系?
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
想一想:(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n
×
n
=
棋子总数
n2
=棋子总数
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
2、摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(15根)
…
平行四边形
多边形
边数
3
4
5
6
内角和
180°
360°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
多边形内角和=(边数-2)×180°
(9-2)×180°=1260°
问题:遇到复杂的问题,你可以怎样思考?
1.
化繁为简
2.
画图、枚举
3.
有序思考
4.
探究规律
五、回顾所学,课堂总结
