二元一次不等式(组)与简单的线性
文档属性
| 名称 | 二元一次不等式(组)与简单的线性 |  | |
| 格式 | rar | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-21 19:33:55 | ||
图片预览


文档简介
(共17张PPT)
3.3.2简单的线性规划问题(一)
1、画出二元一次不等式表示的平面区域的方法:
方法1:直线定界,特殊点定域
方法2:
当B>0, Ax+By+C>0表示在直线的上方区域
当B<0, Ax+By+C>0表示在直线的下方区域
当B=0呢?
复习回顾
2、怎样画不等式组表示的平面区域呢?
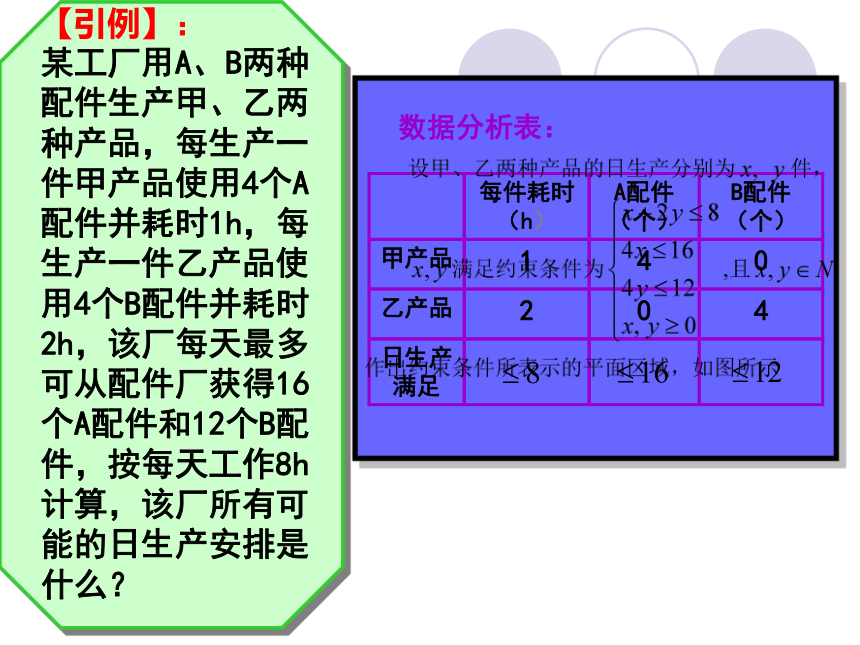
数据分析表:
日生产满足
4
0
2
乙产品
0
4
1
甲产品
B配件(个)
A配件(个)
每件耗时(h)
【引例】:
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
2
4
8
6
4
2
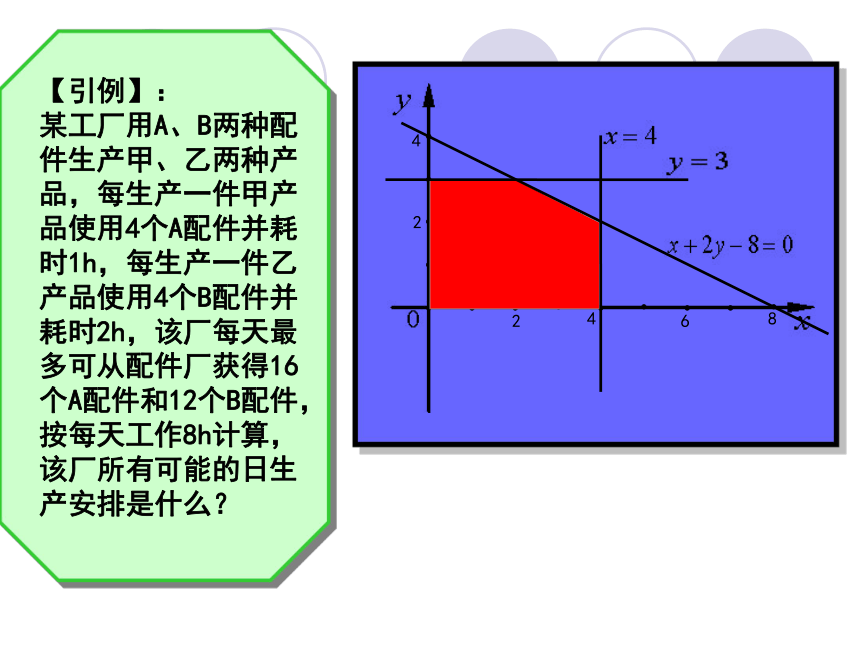
【引例】:
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
2
4
8
6
4
2
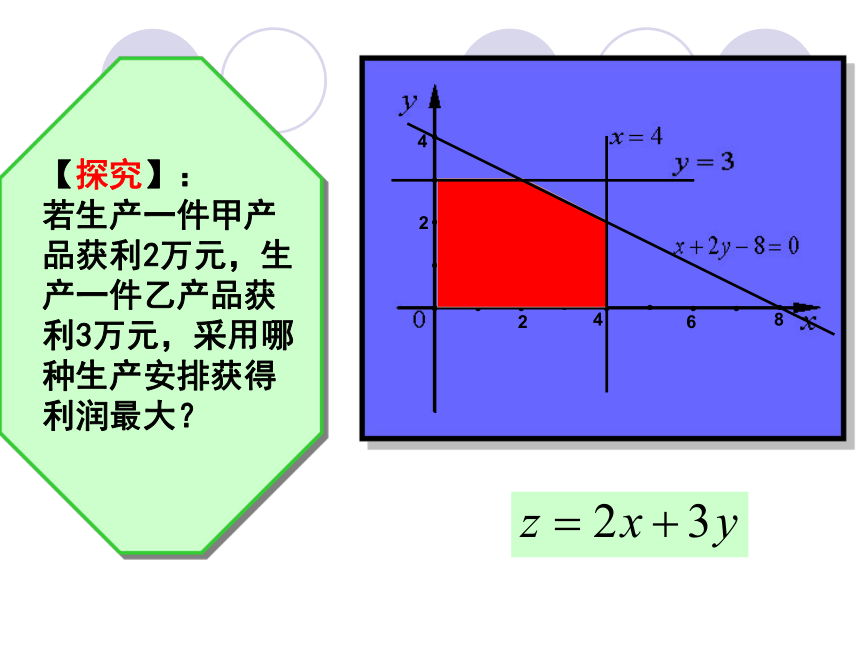
【探究】:
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排获得利润最大?
0
x
y
4
3
4
8
M(4,2)
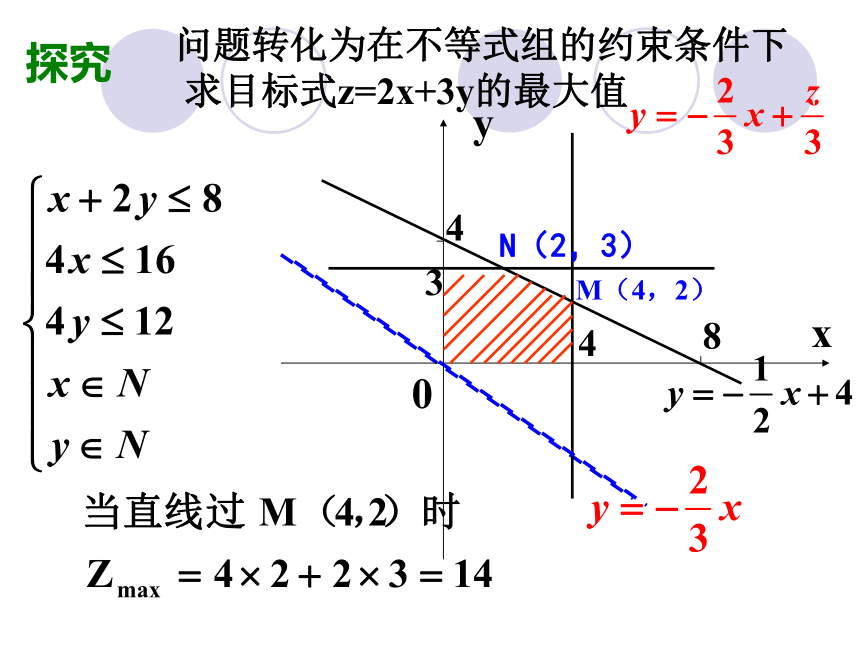
问题转化为在不等式组的约束条件下
求目标式z=2x+3y的最大值
探究
N(2,3)
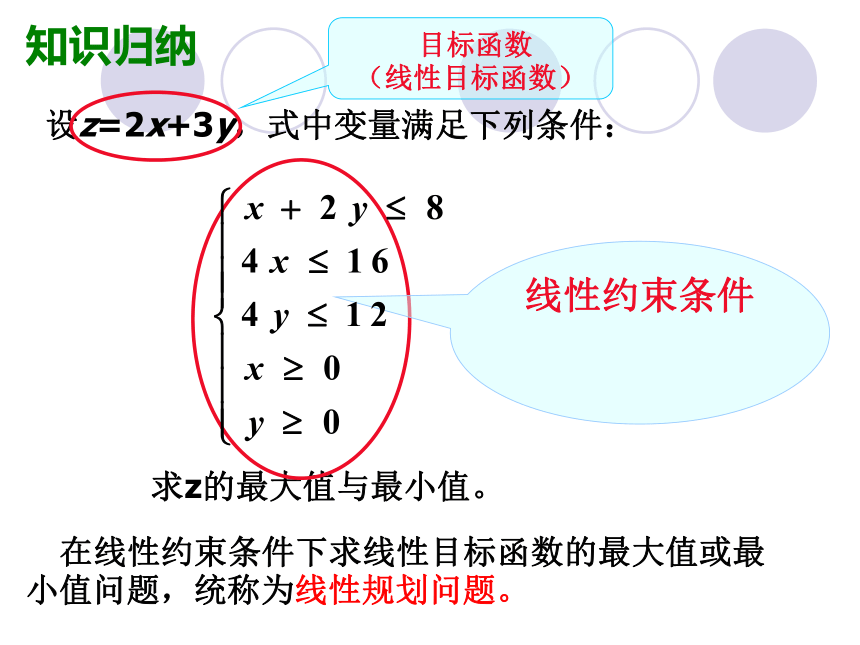
设z=2x+3y,式中变量满足下列条件:
求z的最大值与最小值。
目标函数
(线性目标函数)
线性约束条件
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
知识归纳
y
4
8
4
3
o
可行域
可行解
最优解
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
知识归纳
0
A
B
C
①
在____处有最大值___,
在____处有最小值___;
②
在____处有最大值___,
在____处有最小值___;
请你探究并讨论以下问题:
合作学习
A 6
BC 1
B -3
C 1
例题1.如图,已知
中的三顶点
点
在
内部及边界运动,
x+y=0
四个步骤:画、作、移、答
转化
线性约束条件
可行域
转化
线性目标函数
Z=Ax+By
一组平行线
转化
最优解
求纵截距 的最值
知识归纳
求最优解的方法:
数形结合法
(2)代点验算法(适用于封闭的可行域)
思考与延伸:
已知目标函数是z=2x-ay,可行域如图所示(含边界)
(1)Z取最大值时最优解是(4,2),求a的取值范围。
(2)Z取得最大值的最优解有无数个,求实数a的值。
例题2:求Z=3x+5y的最大值和最小值,
使x,y满足约束条件
解:作出可行域
x
y
o
A
B
C
z=3x+5y
直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
x,y满足约束条件
思考与延伸:
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:平移直线法、代点验算法
1、知识小结:
2、数形结合思想:距离、斜率、截距
作业:
《学法大视野》第29课时
3.3.2简单的线性规划问题(一)
1、画出二元一次不等式表示的平面区域的方法:
方法1:直线定界,特殊点定域
方法2:
当B>0, Ax+By+C>0表示在直线的上方区域
当B<0, Ax+By+C>0表示在直线的下方区域
当B=0呢?
复习回顾
2、怎样画不等式组表示的平面区域呢?
数据分析表:
日生产满足
4
0
2
乙产品
0
4
1
甲产品
B配件(个)
A配件(个)
每件耗时(h)
【引例】:
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
2
4
8
6
4
2
【引例】:
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
2
4
8
6
4
2
【探究】:
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排获得利润最大?
0
x
y
4
3
4
8
M(4,2)
问题转化为在不等式组的约束条件下
求目标式z=2x+3y的最大值
探究
N(2,3)
设z=2x+3y,式中变量满足下列条件:
求z的最大值与最小值。
目标函数
(线性目标函数)
线性约束条件
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
知识归纳
y
4
8
4
3
o
可行域
可行解
最优解
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
知识归纳
0
A
B
C
①
在____处有最大值___,
在____处有最小值___;
②
在____处有最大值___,
在____处有最小值___;
请你探究并讨论以下问题:
合作学习
A 6
BC 1
B -3
C 1
例题1.如图,已知
中的三顶点
点
在
内部及边界运动,
x+y=0
四个步骤:画、作、移、答
转化
线性约束条件
可行域
转化
线性目标函数
Z=Ax+By
一组平行线
转化
最优解
求纵截距 的最值
知识归纳
求最优解的方法:
数形结合法
(2)代点验算法(适用于封闭的可行域)
思考与延伸:
已知目标函数是z=2x-ay,可行域如图所示(含边界)
(1)Z取最大值时最优解是(4,2),求a的取值范围。
(2)Z取得最大值的最优解有无数个,求实数a的值。
例题2:求Z=3x+5y的最大值和最小值,
使x,y满足约束条件
解:作出可行域
x
y
o
A
B
C
z=3x+5y
直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
x,y满足约束条件
思考与延伸:
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:平移直线法、代点验算法
1、知识小结:
2、数形结合思想:距离、斜率、截距
作业:
《学法大视野》第29课时
