高中物理第四章机械能和能源习题课:功能关系的三类典型问题课件 56张PPT
文档属性
| 名称 | 高中物理第四章机械能和能源习题课:功能关系的三类典型问题课件 56张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-25 00:00:00 | ||
图片预览











文档简介
(共55张PPT)
习题课:
功能关系的三类典型问题
一 板块模型中的功能关系
1.模型特点:
(1)系统中的两个组成物体会发生相对运动。
(2)一般是多个物体的多个过程问题。
(3)往往涉及摩擦力做功、动能、内能变化问题。
(4)处理问题常常用到整体法和隔离法。
2.解决思路:
(1)分清有多少种形式的能(如机械能、热能、电能)在变化。
(2)分别找出所有减少的能量和所有增加的能量。
(3)利用增加的能量与减少的能量相等列式计算。
【典例示范】
如图所示,一块足够长的平板放在光滑的水平面上①,其质量M=2
kg,一滑块以v0=12
m/s的初速度冲上平板,滑块的质量m=1
kg,
滑块与平板间的动摩擦因数μ=0.4②,g取10
m/s2。求最终滑块与平板由于摩擦产生的热量③。
【审题关键】
序号
信息提取
①
平板与水平面间无摩擦力
②
滑块在摩擦力作用下减速,而平板是加速
③
最终状态是两者共速一起运动
【解析】滑块的加速度大小:
a1=
=4
m/s2
平板的加速度的大小:
a2=
m/s2=2
m/s2
最终滑块与平板具有共同速度v
则v=v0-a1t,v=a2t
代入数据解得v=4
m/s
由能量守恒定律知:Q=
代入数据得Q=48
J
答案:48
J
【定向训练】
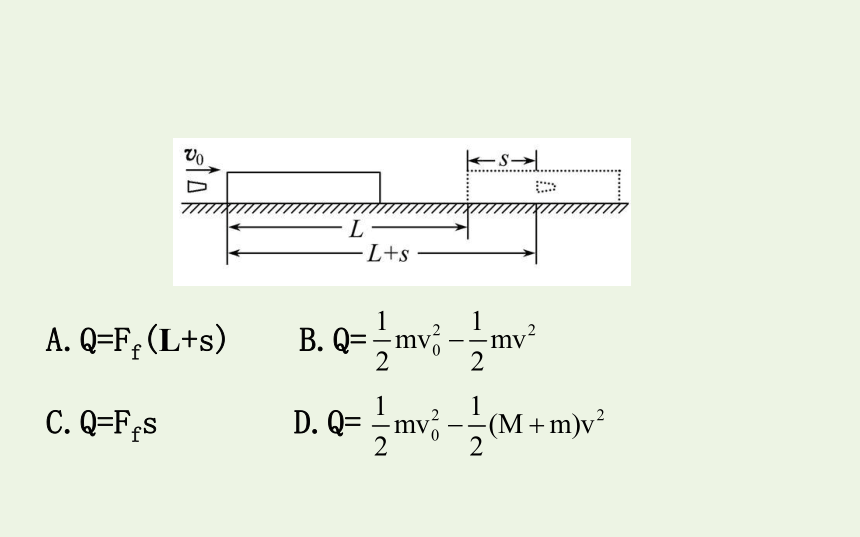
1.(多选)如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0水平射中木块,并最终留在木块中与木块一起以速度v运动。已知当子弹相对木块静止时,木块前进距离L,子弹进入木块的深度为s。若木块对子弹的阻力Ff视为恒定,则在此过程中产生的热量
A.Q=Ff(L+s)
B.Q=
C.Q=Ffs
D.Q=
【解析】选C、D。对木块:FfL=
Mv2
对子弹:-Ff(L+s)=
mv2-
m
联立可得,Ffs=
m
-
(M+m)v2
依据能量转化和守恒定律,Q=
m
-
(M+m)v2
产生的热量Q=Ffs,故C、D正确。
2.如图所示,右端连有一个光滑弧形槽的水平桌面AB长L=1.5
m,一个质量为m=0.5
kg的木块在F=1.5
N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,g取10
m/s2。求:
(1)木块沿弧形槽上升的最大高度(木块未离开弧形槽)。
(2)木块沿弧形槽滑回B端后,在水平桌面上滑动的最大距离。
【解析】(1)设木块沿弧形槽上升的最大高度为h,木块在最高点时的速度为零。从木块开始运动到弧形槽最高点,由动能定理得:
FL-fL-mgh=0
其中f=μN=μmg=0.2×0.5×10
N=1.0
N
所以h=
(2)设木块离开B点后沿桌面滑动的最大距离为x。由动能定理得:mgh-fx=0
所以:x=
m=0.75
m
答案:(1)0.15
m (2)0.75
m
二 含弹簧系统中的功能关系
1.模型特点:
(1)系统中的弹簧发生弹性形变从而具有弹性势能。
(2)弹簧的弹性势能具有对称性。相对于零势能点形变量相等的两点(弹簧仍处于弹性限度内)的弹性势能相等。
(3)弹簧形变量发生变化,弹性势能与其他形式的能发生转化。
2.解决思路:
(1)弹簧弹力做正功,弹簧的弹性势能减少;弹簧弹力做负功,弹簧的弹性势能增加。
(2)弹簧弹力是变力,求弹力做功时,一般从能量的转化和守恒的角度来解决。
(3)当弹簧最长或最短时,物体速度有极值,弹簧的弹性势能最大。
【典例示范】
(多选)(2019·江苏高考)如图所示,
轻质弹簧的左端固定,并处于自然状
态。小物块的质量为m,从A点向左沿水平地面运动,压缩弹簧后被弹回,运动到A点恰好静止。物块向左运动的最大距离为s,与地面间的动摩擦因数为μ,重力加速度为g,弹簧未超出弹性限度。在上述过程中
A.弹簧的最大弹力为μmg
B.物块克服摩擦力做的功为2μmgs
C.弹簧的最大弹性势能为μmgs
D.物块在A点的初速度为
【解析】选B、C。弹簧被压缩到最短时,物块有向右的
加速度,弹力大于滑动摩擦力f=μmg,选项A错误;物块
在运动中所受的摩擦力与运动方向总相反,物块运动的
路程为2s,所以克服摩擦力做的功为W=2μmgs,选项B正
确;由动能定理可知,从弹簧被压缩至最短到物块运动
到A点,动能的变化为零,弹簧的弹性势能等于克服摩擦
力做功W′=μmgs,选项C正确;由物块从A点到返回A点,
根据动能定理-μmg·2s=0-
可得v0=2
,所
以选项D错误。
【定向训练】
1.劲度系数分别为kA=2
000
N/m和
kB=3
000
N/m的弹簧A和B连接在一
起,拉长后将两端固定,如图所示,弹性势能EpA、EpB的关系为
( )
A.EpA=EpB B.EpA=1.5EpB
C.EpA=2EpB
D.EpA=0.5EpB
【解析】选B。弹簧A和B连接在一起,拉长后将两端固
定,根据力的相互性可知,两个弹簧的弹力大小相等。
由于弹簧的弹力大小与弹簧的伸长量之间的关系:F=kx,
所以拉长弹簧的过程中对弹簧做的功:W=F·x=
Fx
=
;
又克服弹簧的弹力做的功等于弹簧增加的
弹性势能,可知,两个弹簧的拉力相等的条件下,弹性势
能与弹簧的劲度系数成反比,则
即EpA=
1.5EpB,故B正确。
2.
(2019·南充高一检测)如图所示,把质量
为m的物体放在竖直放置的弹簧上,并把物体
往下按至位置A保持平衡。
迅速松手后,弹
簧把物体弹起,物体升至最高位置C,途中经
过位置B时弹簧正好处于自由状态。
已知A、B的
高度差h1,B、C的高度差h2,弹簧质量和空气阻力均可忽略,重力加速度为g,取B处所在水平面为零势能面。求:
(1)物体在C处具有的重力势能。
(2)物体在位置A处时弹簧的弹性势能。
(3)物体上升过程中获得最大速度时,弹簧的形变量。(设弹簧劲度系数为k)
【解析】(1)取B处所在水平面为零势能面,则物体在C处具有的重力势能EpC=mgh2。
(2)根据能量关系可知:Ep弹+(-mgh1)=mgh2,解得Ep弹=mg(h1+h2)。
(3)物体速度最大时重力等于弹力,而F=k·Δx
k·Δx=mg,解得:Δx=
。
答案:(1)mgh2 (2)mg(h1+h2) (3)
【补偿训练】
(多选)如图,劲度系数为k的轻质弹簧,
一端系在竖直放置的半径为R的圆环顶
点P,另一端系一质量为m的小球,小球
穿在圆环上做无摩擦的运动。设开始时小球置于A点,弹簧处于自然状态,当小球运动到最低点时速率为v,对圆环恰好没有压力。下列正确的是
( )
A.从A到B的过程中,小球的机械能守恒
B.从A到B的过程中,小球的机械能减少
C.小球过B点时,弹簧的弹力为mg+m
D.小球过B点时,弹簧的弹力为mg+m
【解析】选B、C。运动过程中,弹力对小球做负功,
小球的机械能减少,A错,B对;由牛顿第二定律得F-
mg=m
,故小球过B点时,弹力F=mg+m
,C对,D错。
三 皮带传动模型中的功能关系
1.模型特点:
(1)物块与传送带之间往往存在相对滑动。
(2)物块的运动一般存在多个过程。
(3)一般涉及内能的增加,即摩擦生热。
2.解决思路:
(1)对物块受力分析,明确物块的运动情况。
(2)计算物块和传送带的位移及相对位移。
(3)利用公式Q=fx相对求热量。
【典例示范】
如图所示,皮带的速度是3
m/s,两圆心距离s=4.5
m,现将m=1
kg的小物体轻放在左轮正上方的皮带上,物体与皮带间的动摩擦因数μ=0.15,电动机带动皮带将物体从左轮运送到右轮正上方时,求:
(1)小物体获得的动能Ek。
(2)这一过程摩擦产生的热量Q。
(3)这一过程电动机多消耗的电能E是多少?(g取
10
m/s2)
【解析】(1)对小物体有μmg=ma,得a=1.5
m/s2
速度相等时v=at,t=2
s
x=
at2=3
m<4.5
m
所以小物体应先匀加速后匀速,那么传到右轮正上方
时,Ek=
mv2=4.5
J
(2)只有加速过程受摩擦力,这一过程传送带的路程为
s=vt=6
m
Q=μmg(s-x)=4.5
J
(3)电动机多消耗的电能转化为小物体的动能和摩擦生热
E电=Ek+Q=9
J
答案:(1)4.5
J (2)4.5
J (3)9
J
【定向训练】
1.一条长12
m的传送带,倾角为30°,它能够将工件从地面送到卡车上,每个工件的质量为25
kg,传送带每分钟可传送16个工件,不考虑传送带对工件的加速,g取10
m/s2,则有
( )
A.传送带每分钟对工件做的总功是2.4×104J
B.摩擦力对工件每分钟做的总功是1.2×104J
C.传送带的传送功率为100
W
D.传送带的传送功率为200
W
【解析】选A。传送工件时不计加速,则工件随传送带
一起匀速上升,即摩擦力f=mgsinθ,传送带对工件做功
实质上是传送带的摩擦力f对工件做功。所以W=
nf·l=16×mgsin30°×l=2.4×104
J,A对B错。由功率
定义P=
W=400
W,C、D错。
2.如图所示,一水平方向的传送带以
恒定的速度v=2
m/s沿顺时针方向匀
速转动,传送带右端固定着一光滑的
四分之一圆弧面轨道,并与弧面下端相切。一质量为
m=1
kg的物体自圆弧面轨道的最高点由静止滑下,圆弧
面轨道的半径R=0.45
m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,g取10
m/s2。求:
(1)物体第一次从滑上传送带到离开传送带所经历的时间。
(2)物体第一次从滑上传送带到离开传送带的过程中,传送带对物体做的功。
(3)物体第一次从滑上传送带到离开传送带的过程中,由于摩擦产生的热量。
【解析】(1)沿圆弧面轨道下滑过程中机械能守恒,设物体滑上传送带时的速度为v1,
则mgR=
,得v1=3
m/s,
物体在传送带上运动的加速度
a=
=μg=2
m/s2,
物体在传送带上向左运动的时间t1=
=1.5
s,
向左滑动的最大距离
s物1=
=2.25
m,
物体向右运动速度达到v时,向右运动的距离
s物2=
=1
m,
所用时间t2=
=1
s,
匀速运动的时间t3=
=0.625
s,
所以t=t1+t2+t3=3.125
s
(2)根据动能定理,传送带对物体做的功:
W=
=-2.5
J,
(3)物体在传送带上向左滑动的最大距离
s物1=
=2.25
m
传送带向右运动位移
s带1=vt1=3
m
Δs1=s物1+s带1=5.25
m
物体在传送带上向右运动,加速到与传送带速度相同
过程中
向右运动的距离s物2=
=1
m
s带2=vt2=2
m,Δs2=s带2-s物2=1
m
物体相对传送带运动的位移Δs=Δs1+Δs2=6.25
m
由于摩擦产生的热量Q=μmgΔs=12.5
J
答案:(1)3.125
s
(2)-2.5
J
(3)12.5
J
【补偿训练】
(多选)如图所示,水平桌面上的轻
质弹簧一端固定,另一端与小物块
相连,弹簧处于自然长度时物块位于O点(图中未标
出)。物块的质量为m,AB=a,物块与桌面间的动摩擦
因数为μ。现用水平向右的力将物块从O点拉至A点,拉力做的功为W。撤去拉力后物块由静止向左运动,经O点到达B点时速度为零。重力加速度为g。则上述过程中
( )
A.物块在A点时,弹簧的弹性势能等于W-
μmga
B.物块在B点时,弹簧的弹性势能小于W-
μmga
C.经O点时,物块的动能小于W-μmga
D.物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能
【解析】选B、C。由于摩擦力的存在,A点时的弹性势
能必大于B点时的弹性势能,故弹簧原长的位置即O点一
定在稍靠近B右侧的某点,由O点拉到A点时,克服摩擦力
做的功一定大于
μmga,故物块在A点时,弹簧的弹性
势能小于W-
μmga,A项错误;从A点至B点,机械能继续
减少μmga,故物块在B点时,弹簧的弹性势能小于W-
μmga,B项正确;从A点至O点,克服摩擦力做的功仍
然大于
μmga,故由O至A再由A至O,克服摩擦力做的
功的总量一定大于μmga,故O点的动能小于W-μmga,C项
正确;物块动能最大时,弹力等于摩擦力,而在B点弹力
与摩擦力的大小关系未知,故物块动能最大时弹簧伸长量与物块在B点时弹簧伸长量大小未知,故此两位置弹性势能大小关系无法判断,故D错误。
习题课:
功能关系的三类典型问题
一 板块模型中的功能关系
1.模型特点:
(1)系统中的两个组成物体会发生相对运动。
(2)一般是多个物体的多个过程问题。
(3)往往涉及摩擦力做功、动能、内能变化问题。
(4)处理问题常常用到整体法和隔离法。
2.解决思路:
(1)分清有多少种形式的能(如机械能、热能、电能)在变化。
(2)分别找出所有减少的能量和所有增加的能量。
(3)利用增加的能量与减少的能量相等列式计算。
【典例示范】
如图所示,一块足够长的平板放在光滑的水平面上①,其质量M=2
kg,一滑块以v0=12
m/s的初速度冲上平板,滑块的质量m=1
kg,
滑块与平板间的动摩擦因数μ=0.4②,g取10
m/s2。求最终滑块与平板由于摩擦产生的热量③。
【审题关键】
序号
信息提取
①
平板与水平面间无摩擦力
②
滑块在摩擦力作用下减速,而平板是加速
③
最终状态是两者共速一起运动
【解析】滑块的加速度大小:
a1=
=4
m/s2
平板的加速度的大小:
a2=
m/s2=2
m/s2
最终滑块与平板具有共同速度v
则v=v0-a1t,v=a2t
代入数据解得v=4
m/s
由能量守恒定律知:Q=
代入数据得Q=48
J
答案:48
J
【定向训练】
1.(多选)如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0水平射中木块,并最终留在木块中与木块一起以速度v运动。已知当子弹相对木块静止时,木块前进距离L,子弹进入木块的深度为s。若木块对子弹的阻力Ff视为恒定,则在此过程中产生的热量
A.Q=Ff(L+s)
B.Q=
C.Q=Ffs
D.Q=
【解析】选C、D。对木块:FfL=
Mv2
对子弹:-Ff(L+s)=
mv2-
m
联立可得,Ffs=
m
-
(M+m)v2
依据能量转化和守恒定律,Q=
m
-
(M+m)v2
产生的热量Q=Ffs,故C、D正确。
2.如图所示,右端连有一个光滑弧形槽的水平桌面AB长L=1.5
m,一个质量为m=0.5
kg的木块在F=1.5
N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,g取10
m/s2。求:
(1)木块沿弧形槽上升的最大高度(木块未离开弧形槽)。
(2)木块沿弧形槽滑回B端后,在水平桌面上滑动的最大距离。
【解析】(1)设木块沿弧形槽上升的最大高度为h,木块在最高点时的速度为零。从木块开始运动到弧形槽最高点,由动能定理得:
FL-fL-mgh=0
其中f=μN=μmg=0.2×0.5×10
N=1.0
N
所以h=
(2)设木块离开B点后沿桌面滑动的最大距离为x。由动能定理得:mgh-fx=0
所以:x=
m=0.75
m
答案:(1)0.15
m (2)0.75
m
二 含弹簧系统中的功能关系
1.模型特点:
(1)系统中的弹簧发生弹性形变从而具有弹性势能。
(2)弹簧的弹性势能具有对称性。相对于零势能点形变量相等的两点(弹簧仍处于弹性限度内)的弹性势能相等。
(3)弹簧形变量发生变化,弹性势能与其他形式的能发生转化。
2.解决思路:
(1)弹簧弹力做正功,弹簧的弹性势能减少;弹簧弹力做负功,弹簧的弹性势能增加。
(2)弹簧弹力是变力,求弹力做功时,一般从能量的转化和守恒的角度来解决。
(3)当弹簧最长或最短时,物体速度有极值,弹簧的弹性势能最大。
【典例示范】
(多选)(2019·江苏高考)如图所示,
轻质弹簧的左端固定,并处于自然状
态。小物块的质量为m,从A点向左沿水平地面运动,压缩弹簧后被弹回,运动到A点恰好静止。物块向左运动的最大距离为s,与地面间的动摩擦因数为μ,重力加速度为g,弹簧未超出弹性限度。在上述过程中
A.弹簧的最大弹力为μmg
B.物块克服摩擦力做的功为2μmgs
C.弹簧的最大弹性势能为μmgs
D.物块在A点的初速度为
【解析】选B、C。弹簧被压缩到最短时,物块有向右的
加速度,弹力大于滑动摩擦力f=μmg,选项A错误;物块
在运动中所受的摩擦力与运动方向总相反,物块运动的
路程为2s,所以克服摩擦力做的功为W=2μmgs,选项B正
确;由动能定理可知,从弹簧被压缩至最短到物块运动
到A点,动能的变化为零,弹簧的弹性势能等于克服摩擦
力做功W′=μmgs,选项C正确;由物块从A点到返回A点,
根据动能定理-μmg·2s=0-
可得v0=2
,所
以选项D错误。
【定向训练】
1.劲度系数分别为kA=2
000
N/m和
kB=3
000
N/m的弹簧A和B连接在一
起,拉长后将两端固定,如图所示,弹性势能EpA、EpB的关系为
( )
A.EpA=EpB B.EpA=1.5EpB
C.EpA=2EpB
D.EpA=0.5EpB
【解析】选B。弹簧A和B连接在一起,拉长后将两端固
定,根据力的相互性可知,两个弹簧的弹力大小相等。
由于弹簧的弹力大小与弹簧的伸长量之间的关系:F=kx,
所以拉长弹簧的过程中对弹簧做的功:W=F·x=
Fx
=
;
又克服弹簧的弹力做的功等于弹簧增加的
弹性势能,可知,两个弹簧的拉力相等的条件下,弹性势
能与弹簧的劲度系数成反比,则
即EpA=
1.5EpB,故B正确。
2.
(2019·南充高一检测)如图所示,把质量
为m的物体放在竖直放置的弹簧上,并把物体
往下按至位置A保持平衡。
迅速松手后,弹
簧把物体弹起,物体升至最高位置C,途中经
过位置B时弹簧正好处于自由状态。
已知A、B的
高度差h1,B、C的高度差h2,弹簧质量和空气阻力均可忽略,重力加速度为g,取B处所在水平面为零势能面。求:
(1)物体在C处具有的重力势能。
(2)物体在位置A处时弹簧的弹性势能。
(3)物体上升过程中获得最大速度时,弹簧的形变量。(设弹簧劲度系数为k)
【解析】(1)取B处所在水平面为零势能面,则物体在C处具有的重力势能EpC=mgh2。
(2)根据能量关系可知:Ep弹+(-mgh1)=mgh2,解得Ep弹=mg(h1+h2)。
(3)物体速度最大时重力等于弹力,而F=k·Δx
k·Δx=mg,解得:Δx=
。
答案:(1)mgh2 (2)mg(h1+h2) (3)
【补偿训练】
(多选)如图,劲度系数为k的轻质弹簧,
一端系在竖直放置的半径为R的圆环顶
点P,另一端系一质量为m的小球,小球
穿在圆环上做无摩擦的运动。设开始时小球置于A点,弹簧处于自然状态,当小球运动到最低点时速率为v,对圆环恰好没有压力。下列正确的是
( )
A.从A到B的过程中,小球的机械能守恒
B.从A到B的过程中,小球的机械能减少
C.小球过B点时,弹簧的弹力为mg+m
D.小球过B点时,弹簧的弹力为mg+m
【解析】选B、C。运动过程中,弹力对小球做负功,
小球的机械能减少,A错,B对;由牛顿第二定律得F-
mg=m
,故小球过B点时,弹力F=mg+m
,C对,D错。
三 皮带传动模型中的功能关系
1.模型特点:
(1)物块与传送带之间往往存在相对滑动。
(2)物块的运动一般存在多个过程。
(3)一般涉及内能的增加,即摩擦生热。
2.解决思路:
(1)对物块受力分析,明确物块的运动情况。
(2)计算物块和传送带的位移及相对位移。
(3)利用公式Q=fx相对求热量。
【典例示范】
如图所示,皮带的速度是3
m/s,两圆心距离s=4.5
m,现将m=1
kg的小物体轻放在左轮正上方的皮带上,物体与皮带间的动摩擦因数μ=0.15,电动机带动皮带将物体从左轮运送到右轮正上方时,求:
(1)小物体获得的动能Ek。
(2)这一过程摩擦产生的热量Q。
(3)这一过程电动机多消耗的电能E是多少?(g取
10
m/s2)
【解析】(1)对小物体有μmg=ma,得a=1.5
m/s2
速度相等时v=at,t=2
s
x=
at2=3
m<4.5
m
所以小物体应先匀加速后匀速,那么传到右轮正上方
时,Ek=
mv2=4.5
J
(2)只有加速过程受摩擦力,这一过程传送带的路程为
s=vt=6
m
Q=μmg(s-x)=4.5
J
(3)电动机多消耗的电能转化为小物体的动能和摩擦生热
E电=Ek+Q=9
J
答案:(1)4.5
J (2)4.5
J (3)9
J
【定向训练】
1.一条长12
m的传送带,倾角为30°,它能够将工件从地面送到卡车上,每个工件的质量为25
kg,传送带每分钟可传送16个工件,不考虑传送带对工件的加速,g取10
m/s2,则有
( )
A.传送带每分钟对工件做的总功是2.4×104J
B.摩擦力对工件每分钟做的总功是1.2×104J
C.传送带的传送功率为100
W
D.传送带的传送功率为200
W
【解析】选A。传送工件时不计加速,则工件随传送带
一起匀速上升,即摩擦力f=mgsinθ,传送带对工件做功
实质上是传送带的摩擦力f对工件做功。所以W=
nf·l=16×mgsin30°×l=2.4×104
J,A对B错。由功率
定义P=
W=400
W,C、D错。
2.如图所示,一水平方向的传送带以
恒定的速度v=2
m/s沿顺时针方向匀
速转动,传送带右端固定着一光滑的
四分之一圆弧面轨道,并与弧面下端相切。一质量为
m=1
kg的物体自圆弧面轨道的最高点由静止滑下,圆弧
面轨道的半径R=0.45
m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,g取10
m/s2。求:
(1)物体第一次从滑上传送带到离开传送带所经历的时间。
(2)物体第一次从滑上传送带到离开传送带的过程中,传送带对物体做的功。
(3)物体第一次从滑上传送带到离开传送带的过程中,由于摩擦产生的热量。
【解析】(1)沿圆弧面轨道下滑过程中机械能守恒,设物体滑上传送带时的速度为v1,
则mgR=
,得v1=3
m/s,
物体在传送带上运动的加速度
a=
=μg=2
m/s2,
物体在传送带上向左运动的时间t1=
=1.5
s,
向左滑动的最大距离
s物1=
=2.25
m,
物体向右运动速度达到v时,向右运动的距离
s物2=
=1
m,
所用时间t2=
=1
s,
匀速运动的时间t3=
=0.625
s,
所以t=t1+t2+t3=3.125
s
(2)根据动能定理,传送带对物体做的功:
W=
=-2.5
J,
(3)物体在传送带上向左滑动的最大距离
s物1=
=2.25
m
传送带向右运动位移
s带1=vt1=3
m
Δs1=s物1+s带1=5.25
m
物体在传送带上向右运动,加速到与传送带速度相同
过程中
向右运动的距离s物2=
=1
m
s带2=vt2=2
m,Δs2=s带2-s物2=1
m
物体相对传送带运动的位移Δs=Δs1+Δs2=6.25
m
由于摩擦产生的热量Q=μmgΔs=12.5
J
答案:(1)3.125
s
(2)-2.5
J
(3)12.5
J
【补偿训练】
(多选)如图所示,水平桌面上的轻
质弹簧一端固定,另一端与小物块
相连,弹簧处于自然长度时物块位于O点(图中未标
出)。物块的质量为m,AB=a,物块与桌面间的动摩擦
因数为μ。现用水平向右的力将物块从O点拉至A点,拉力做的功为W。撤去拉力后物块由静止向左运动,经O点到达B点时速度为零。重力加速度为g。则上述过程中
( )
A.物块在A点时,弹簧的弹性势能等于W-
μmga
B.物块在B点时,弹簧的弹性势能小于W-
μmga
C.经O点时,物块的动能小于W-μmga
D.物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能
【解析】选B、C。由于摩擦力的存在,A点时的弹性势
能必大于B点时的弹性势能,故弹簧原长的位置即O点一
定在稍靠近B右侧的某点,由O点拉到A点时,克服摩擦力
做的功一定大于
μmga,故物块在A点时,弹簧的弹性
势能小于W-
μmga,A项错误;从A点至B点,机械能继续
减少μmga,故物块在B点时,弹簧的弹性势能小于W-
μmga,B项正确;从A点至O点,克服摩擦力做的功仍
然大于
μmga,故由O至A再由A至O,克服摩擦力做的
功的总量一定大于μmga,故O点的动能小于W-μmga,C项
正确;物块动能最大时,弹力等于摩擦力,而在B点弹力
与摩擦力的大小关系未知,故物块动能最大时弹簧伸长量与物块在B点时弹簧伸长量大小未知,故此两位置弹性势能大小关系无法判断,故D错误。
