11.2 简谐运动的描述—人教版高中物理选修3-4课件(共21张PPT)
文档属性
| 名称 | 11.2 简谐运动的描述—人教版高中物理选修3-4课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 925.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-25 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
二、简谐运动的描述
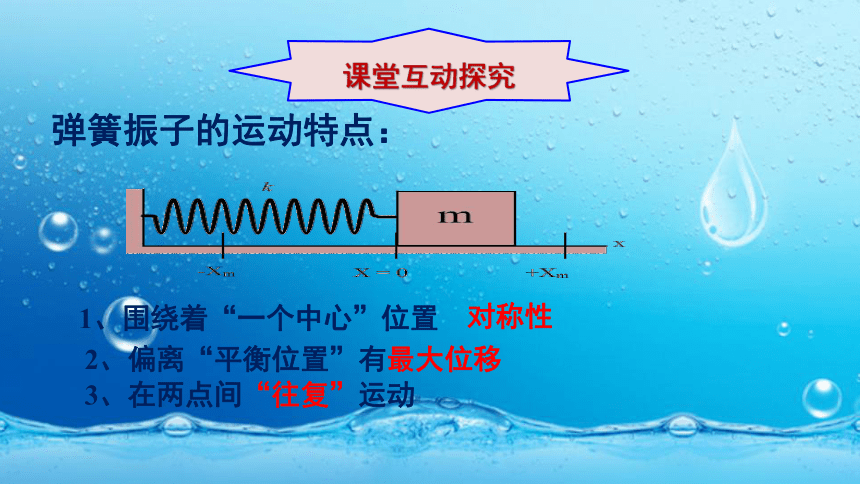
课堂互动探究
弹簧振子的运动特点:
1、围绕着“一个中心”位置
2、偏离“平衡位置”有最大位移
3、在两点间“往复”运动
对称性
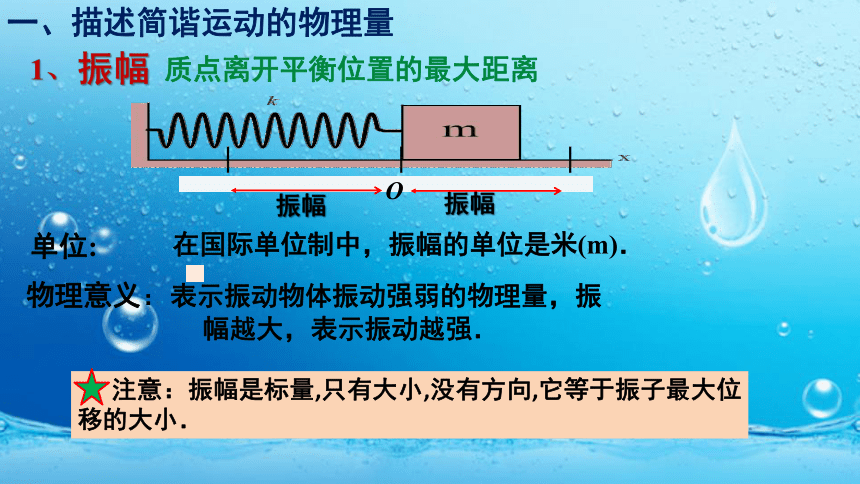
一、描述简谐运动的物理量
1、
质点离开平衡位置的最大距离
振幅
振幅
振幅
O
单位:
在国际单位制中,振幅的单位是米(m).
物理意义:表示振动物体振动强弱的物理量,振
幅越大,表示振动越强.
注意:振幅是标量,只有大小,没有方向,它等于振子最大位移的大小.
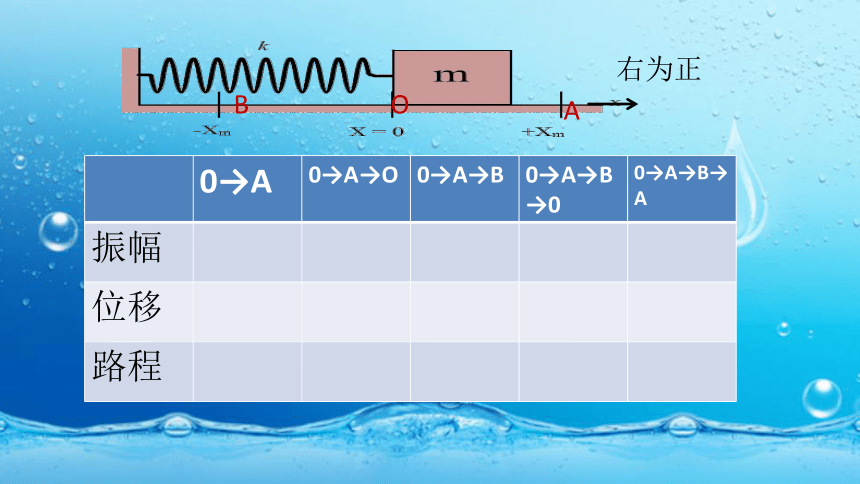
一、描述简谐运动的物理量
振幅
位移
路程
定义
振动物体离开平衡位置的最大距离
从平衡位置指向振子所在位置的有向线段
运动轨迹的长度
矢、标性
标量
矢量
标量
变化
在稳定的振动系统中不发生变化
大小和方向随时间做周期性变化
随时间增加
联系
(1)振幅等于位移最大值的数值;(2)振子在一个周期内的路程等于4个振幅;而振子在一个周期内的位移等于零。
0→A
0→A→O
0→A→B
0→A→B→0
0→A→B→A
振幅
位移
路程
O
A
B
右为正
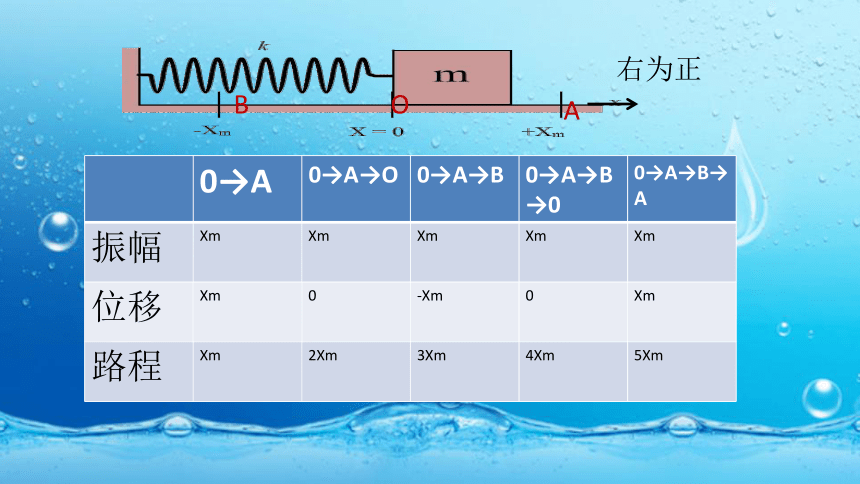
0→A
0→A→O
0→A→B
0→A→B→0
0→A→B→A
振幅
Xm
Xm
Xm
Xm
Xm
位移
Xm
0
-Xm
0
Xm
路程
Xm
2Xm
3Xm
4Xm
5Xm
O
A
B
右为正
一、描述简谐运动的物理量
振幅
振幅
O
2、周期(频率)
振子进行一次完整的振动(全振动)所经历的时间
一、描述简谐运动的物理量
3、相位
位置
用来描述周期性运动在各个时刻所处的不同状态.其单位是弧度(或度)
一、描述简谐运动的物理量
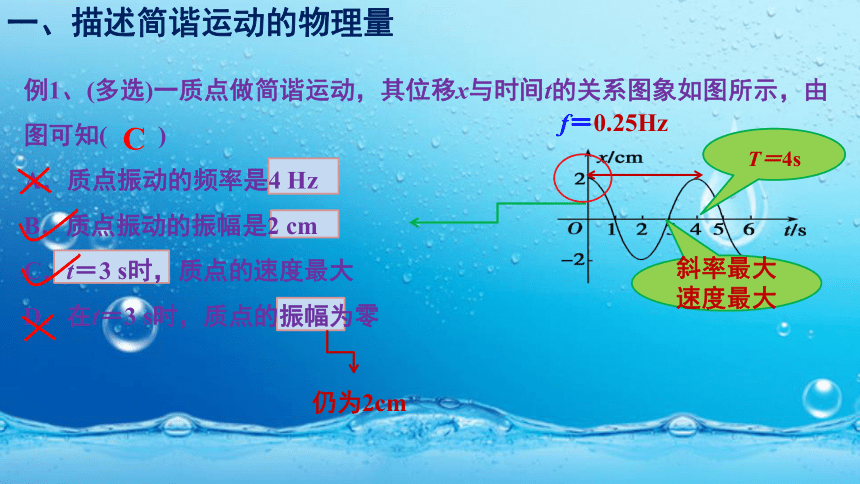
例1、(多选)一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知( )
A.质点振动的频率是4
Hz
B.质点振动的振幅是2
cm
C.t=3
s时,质点的速度最大
D.在t=3
s时,质点的振幅为零
C
f=0.25Hz
仍为2cm
T=4s
斜率最大速度最大
二、简谐运动的表达式
振幅
圆频率
初相位
相位
二、简谐运动的表达式
6.相位差:即某一时刻的相位之差.两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
特别提醒:相位差的取值范围一般为-π≤Δφ≤π,当Δφ=0时两运动步调完全相同,称为同相,当Δφ=π(或-π)时,两运动步调相反,称为反相.
二、简谐运动的表达式
例2、(多选)物体A做简谐运动的振动位移xA=3sin(100t+
)m,物体B做简谐运动的振动位移xB=5sin(100t+
)m,比较A、B的运动( )
A.振幅是矢量,A的振幅是6
m,B的振幅是10
m
B.周期是标量,A、B的周期都是100
s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位
标量
A是3m,B是5m
A是3m,B是5m
CD
二、简谐运动的表达式
例3、一物体沿x轴做简谐运动,振幅为8
cm,频率为0.5
Hz,在t=0时位移是4
cm.且向x轴负向运动,试写出用正弦函数表示的振动方程.
解析
x=Asin(ωt+φ)
A=8cm
f=0.5Hz
x=0.08
sin(πt+φ)m
ω=2πf=π
将t=0时,x=0.04
m代入得
0.04=0.08
sinφ
解得初相φ=
或
.
位移在减小
所求振动方程为:
科学漫步——月相
1、随着月亮每天在星空中自西向东移动,在地球上看,它的形状从圆到缺,又从缺到圆周期性地变化着,周期为29.5天,这就是月亮位相的变化,叫做月相。
2、随着月亮相对于地球和太阳的位置变化,使它被太阳照亮的一面有时朝向地球,有时背向地球;朝向地球的月亮部分有时大一些,有时小一些,这样就出现了不同的月相。
科学漫步——月相
1、朔——当月球运行到太阳与地球之间,被太阳照亮的半球背对着地球,此时地球上的人们就看不到月球,这一天称为“新月”,也叫“朔日”,即农历初一。
2、上弦——随后,月球自西向东逐渐远离太阳,到了农历初七、八,半个亮区对着地球,人们可以看到半个月亮(凸面向西),这一月相叫“上弦月”。
3、望——当月球运行到地球的背日方向,即农历十五、十六、十七,月球的亮区全部对着地球,我们能看到一轮圆月,这一月相称为“满月”,也叫“望”。
4、下弦——满月过后,月球逐渐向太阳靠拢,亮区西侧开始亏缺,到农历二十二、二十三,又能看到半个月亮(凸面向东),这一月相叫做“下弦月”。
出现在黄昏
出现在清晨
1、下列关于振幅的说法中正确的有(
)
A、振幅是振动物体离开平衡位置的最大位移
B、振动物体所经过的路程始终大于振幅
C、振幅是振动物体最大位移的绝对值
D、简谐振动的振幅随时间呈周期性变化
C
课堂练习
CD
课堂练习
2、一个质点在平衡位置0点附近做简谐运动,若从0点开始计时,经过3s质点第一次经过M点;若再继续运动,又经过2s它第二次经过M点;则质点第三次经过M点所需要的时间是(
)
A、8s
B、16s
C、14s
D、(10/3)s
s
s
写出振动方程.
x=10sin(2πt+π/2)
(cm)
课堂练习
3、一弹簧振子的位移随时间变化的图线如下图所示,试写出相应的函数表达式。
4、(多选)如图所示,弹簧振子以O为平衡位置,在BC间振动,则
( )
A.从B→O→C→O→B为一次全振动
B.从O→B→O→C→B为一次全振动
C.从C→O→B→O→C为一次全振动
D.OB的大小不一定等于OC
路程为4个振幅
一定
AC
课堂练习
5、两个简谐运动分别为x1=4asin(4πbt+
)和x2=2asin(4πbt+
),求它们的振幅之比,各自的频率,以及它们的相位差。
解析
振幅之比=
x=Asin(ωt+φ)
两者频率均为:
两者相位差为:
两振动为反相
课堂练习
6、一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13
s质点第一次通过M点,再经0.1
s第二次通过M点,则质点振动周期是多少?
解析
(1)若质点从O点向右运动到M点,
如甲、乙图所示
O→M→A历时0.18s
根据对称性可得到周期T1=4×0.18
s=0.72
s
(2)若质点从O点向左运动到M点,如丙图所示
由O→A→M历时t1=0.13
s
由M→A历时t2=0.05
s,
课堂练习
二、简谐运动的描述
课堂互动探究
弹簧振子的运动特点:
1、围绕着“一个中心”位置
2、偏离“平衡位置”有最大位移
3、在两点间“往复”运动
对称性
一、描述简谐运动的物理量
1、
质点离开平衡位置的最大距离
振幅
振幅
振幅
O
单位:
在国际单位制中,振幅的单位是米(m).
物理意义:表示振动物体振动强弱的物理量,振
幅越大,表示振动越强.
注意:振幅是标量,只有大小,没有方向,它等于振子最大位移的大小.
一、描述简谐运动的物理量
振幅
位移
路程
定义
振动物体离开平衡位置的最大距离
从平衡位置指向振子所在位置的有向线段
运动轨迹的长度
矢、标性
标量
矢量
标量
变化
在稳定的振动系统中不发生变化
大小和方向随时间做周期性变化
随时间增加
联系
(1)振幅等于位移最大值的数值;(2)振子在一个周期内的路程等于4个振幅;而振子在一个周期内的位移等于零。
0→A
0→A→O
0→A→B
0→A→B→0
0→A→B→A
振幅
位移
路程
O
A
B
右为正
0→A
0→A→O
0→A→B
0→A→B→0
0→A→B→A
振幅
Xm
Xm
Xm
Xm
Xm
位移
Xm
0
-Xm
0
Xm
路程
Xm
2Xm
3Xm
4Xm
5Xm
O
A
B
右为正
一、描述简谐运动的物理量
振幅
振幅
O
2、周期(频率)
振子进行一次完整的振动(全振动)所经历的时间
一、描述简谐运动的物理量
3、相位
位置
用来描述周期性运动在各个时刻所处的不同状态.其单位是弧度(或度)
一、描述简谐运动的物理量
例1、(多选)一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知( )
A.质点振动的频率是4
Hz
B.质点振动的振幅是2
cm
C.t=3
s时,质点的速度最大
D.在t=3
s时,质点的振幅为零
C
f=0.25Hz
仍为2cm
T=4s
斜率最大速度最大
二、简谐运动的表达式
振幅
圆频率
初相位
相位
二、简谐运动的表达式
6.相位差:即某一时刻的相位之差.两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
特别提醒:相位差的取值范围一般为-π≤Δφ≤π,当Δφ=0时两运动步调完全相同,称为同相,当Δφ=π(或-π)时,两运动步调相反,称为反相.
二、简谐运动的表达式
例2、(多选)物体A做简谐运动的振动位移xA=3sin(100t+
)m,物体B做简谐运动的振动位移xB=5sin(100t+
)m,比较A、B的运动( )
A.振幅是矢量,A的振幅是6
m,B的振幅是10
m
B.周期是标量,A、B的周期都是100
s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位
标量
A是3m,B是5m
A是3m,B是5m
CD
二、简谐运动的表达式
例3、一物体沿x轴做简谐运动,振幅为8
cm,频率为0.5
Hz,在t=0时位移是4
cm.且向x轴负向运动,试写出用正弦函数表示的振动方程.
解析
x=Asin(ωt+φ)
A=8cm
f=0.5Hz
x=0.08
sin(πt+φ)m
ω=2πf=π
将t=0时,x=0.04
m代入得
0.04=0.08
sinφ
解得初相φ=
或
.
位移在减小
所求振动方程为:
科学漫步——月相
1、随着月亮每天在星空中自西向东移动,在地球上看,它的形状从圆到缺,又从缺到圆周期性地变化着,周期为29.5天,这就是月亮位相的变化,叫做月相。
2、随着月亮相对于地球和太阳的位置变化,使它被太阳照亮的一面有时朝向地球,有时背向地球;朝向地球的月亮部分有时大一些,有时小一些,这样就出现了不同的月相。
科学漫步——月相
1、朔——当月球运行到太阳与地球之间,被太阳照亮的半球背对着地球,此时地球上的人们就看不到月球,这一天称为“新月”,也叫“朔日”,即农历初一。
2、上弦——随后,月球自西向东逐渐远离太阳,到了农历初七、八,半个亮区对着地球,人们可以看到半个月亮(凸面向西),这一月相叫“上弦月”。
3、望——当月球运行到地球的背日方向,即农历十五、十六、十七,月球的亮区全部对着地球,我们能看到一轮圆月,这一月相称为“满月”,也叫“望”。
4、下弦——满月过后,月球逐渐向太阳靠拢,亮区西侧开始亏缺,到农历二十二、二十三,又能看到半个月亮(凸面向东),这一月相叫做“下弦月”。
出现在黄昏
出现在清晨
1、下列关于振幅的说法中正确的有(
)
A、振幅是振动物体离开平衡位置的最大位移
B、振动物体所经过的路程始终大于振幅
C、振幅是振动物体最大位移的绝对值
D、简谐振动的振幅随时间呈周期性变化
C
课堂练习
CD
课堂练习
2、一个质点在平衡位置0点附近做简谐运动,若从0点开始计时,经过3s质点第一次经过M点;若再继续运动,又经过2s它第二次经过M点;则质点第三次经过M点所需要的时间是(
)
A、8s
B、16s
C、14s
D、(10/3)s
s
s
写出振动方程.
x=10sin(2πt+π/2)
(cm)
课堂练习
3、一弹簧振子的位移随时间变化的图线如下图所示,试写出相应的函数表达式。
4、(多选)如图所示,弹簧振子以O为平衡位置,在BC间振动,则
( )
A.从B→O→C→O→B为一次全振动
B.从O→B→O→C→B为一次全振动
C.从C→O→B→O→C为一次全振动
D.OB的大小不一定等于OC
路程为4个振幅
一定
AC
课堂练习
5、两个简谐运动分别为x1=4asin(4πbt+
)和x2=2asin(4πbt+
),求它们的振幅之比,各自的频率,以及它们的相位差。
解析
振幅之比=
x=Asin(ωt+φ)
两者频率均为:
两者相位差为:
两振动为反相
课堂练习
6、一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13
s质点第一次通过M点,再经0.1
s第二次通过M点,则质点振动周期是多少?
解析
(1)若质点从O点向右运动到M点,
如甲、乙图所示
O→M→A历时0.18s
根据对称性可得到周期T1=4×0.18
s=0.72
s
(2)若质点从O点向左运动到M点,如丙图所示
由O→A→M历时t1=0.13
s
由M→A历时t2=0.05
s,
课堂练习
