9.5解直角三角形的应用

9.5解直角三角形的应用4
山东单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一 学习目标：
1能够应用解直角三角形的知识解决实际生活中的测高问题和航海问题。
2经历将实际问题转化为数学问题，然后利用数学 知识加以解决的过程。
二自主预习：
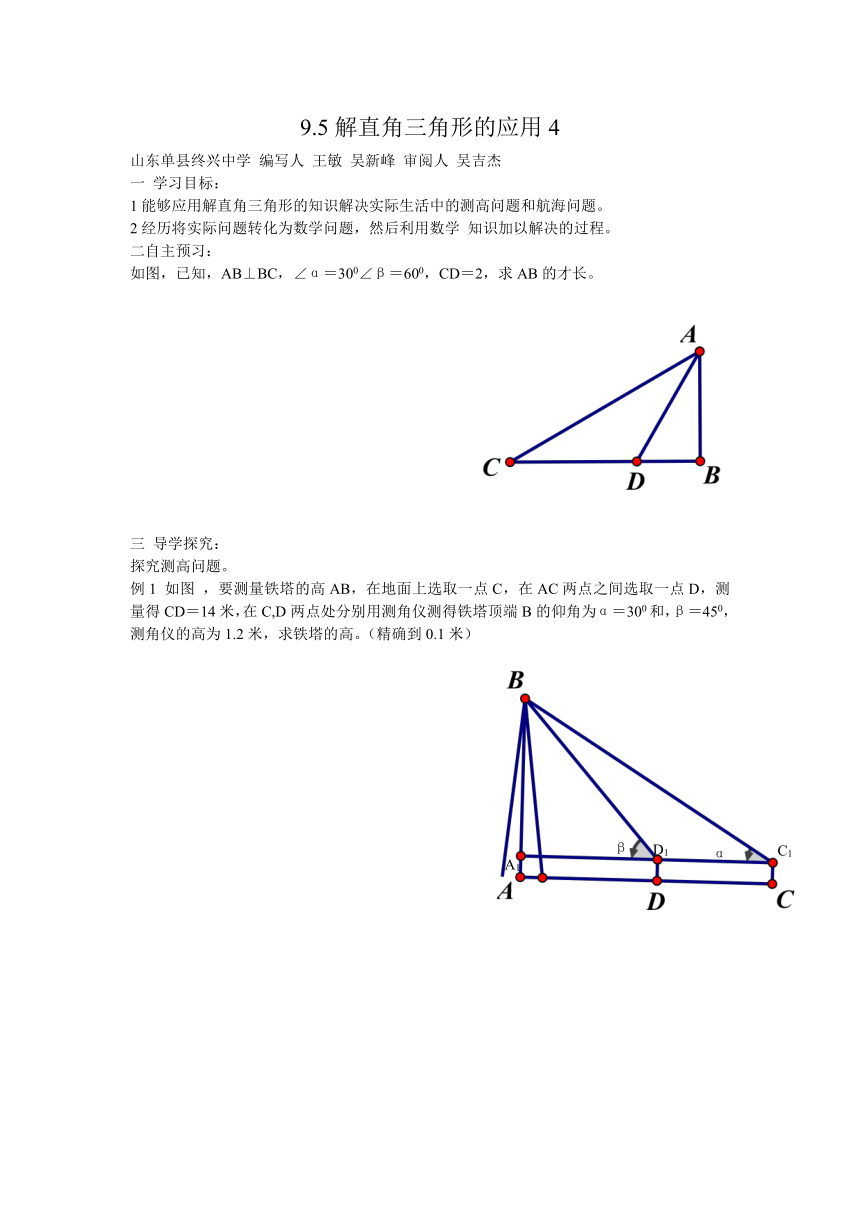
如图，已知，AB⊥BC，∠α＝300∠β＝600，CD＝2，求AB的才长。
三 导学探究：
探究测高问题。
例1 如图 ，要测量铁塔的高AB，在地面上选取一点C，在AC两点之间选取一点D，测量得CD＝14米，在C,D两点处分别用测角仪测得铁塔顶端B的仰角为α＝300和，β＝450，测角仪的高为1.2米，求铁塔的高。（精确到0.1米）
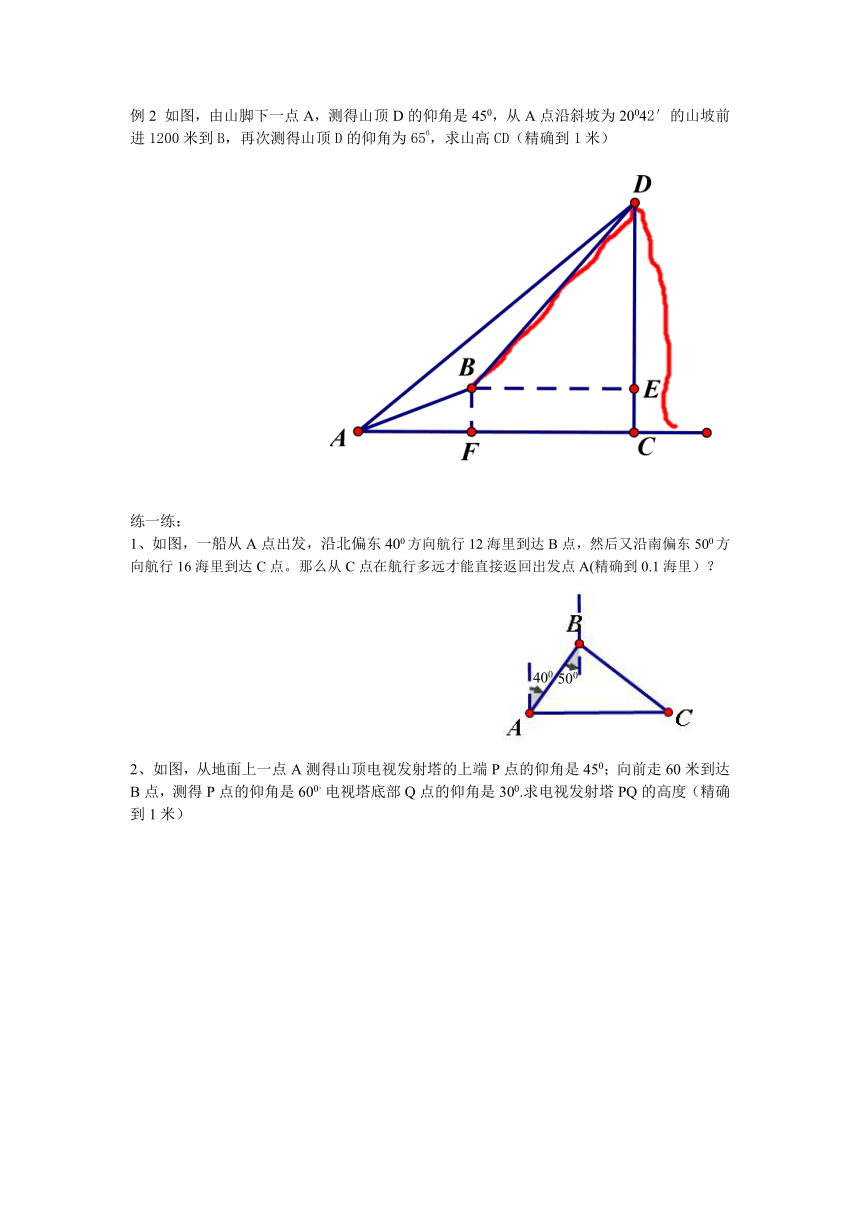
例2 如图，由山脚下一点A，测得山顶D的仰角是450，从A点沿斜坡为20042′的山坡前进1200米到B，再次测得山顶D的仰角为650，求山高CD（精确到1米）
练一练：
1、如图，一船从A点出发，沿北偏东400方向航行12海里到达B点，然后又沿南偏东500方向航行16海里到达C点。那么从C点在航行多远才能直接返回出发点A(精确到0.1海里）？
如图，从地面上一点A测得山顶电视发射塔的上端P点的仰角是450；向前走60米到达B点，测得P点的仰角是600，电视塔底部Q点的仰角是300.求电视发射塔PQ的高度（精确到1米）
四 当堂达标
1 一艘船向正北航行，在A处看到灯塔S在船的北偏东300的方向上，航行12海里到达B处，在B处看到灯塔S在船的北偏东600的方向上，此船继续沿正北方向航行过程中距灯塔S的最近距离是 海里（不作近似计算）
2 在一次测量活动中，同学们要测量某公园湖的码头A与它的正东方向的亭子B之间的距离，如图，他们选择了与码头A、亭子B在同一水平面上的点P，在点P处测量码头A位于点P北偏西300方向，亭子B位于点P北偏东430方向；又测得点P与码头A之间的距离为200米，请你运用以上测得的数据求出码头A与亭子B之间的距离。（结果精确到1米，参考数据：≈1.732 ，tan430≈0.933）
（1题图） （2题图）
3如图，小明想知道湖中两个小亭A、B之间的距离，他在与小亭A、B 位于同一水平面且东西走向的湖边小道l上某一观测点M处，测得亭A、B
C111
D1
A1
α
β
500
400
300
600
450
300
600