六年级下册数学课件-信息窗三(圆锥的体积) 青岛(六三)版 (共27张PPT)
文档属性
| 名称 | 六年级下册数学课件-信息窗三(圆锥的体积) 青岛(六三)版 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 721.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-26 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
圆锥的体积
温故知新
1、圆柱的体积等于(
),用字母表示为(
)或(
)。
2、已知圆柱的体积和底面积,求高可以用公式(
)。
3、已知圆柱的体积和高,求表面积可以用公式(
)。
4、圆锥有什么特点?
h=v÷s
底面积×高
V=sh
V=兀r2h
s=v÷h
学习目标
长方体的体积=底面积×高
圆柱的体积
=
底面积×高
V
=
Sh
1、观察手中的实验工具,看看圆柱和圆锥的底面积和高有着怎样的关系?
2、利用手中的圆柱和圆锥学具探究二者之间体积的关系,并完成实验表格。
群学
–展示
学习提示
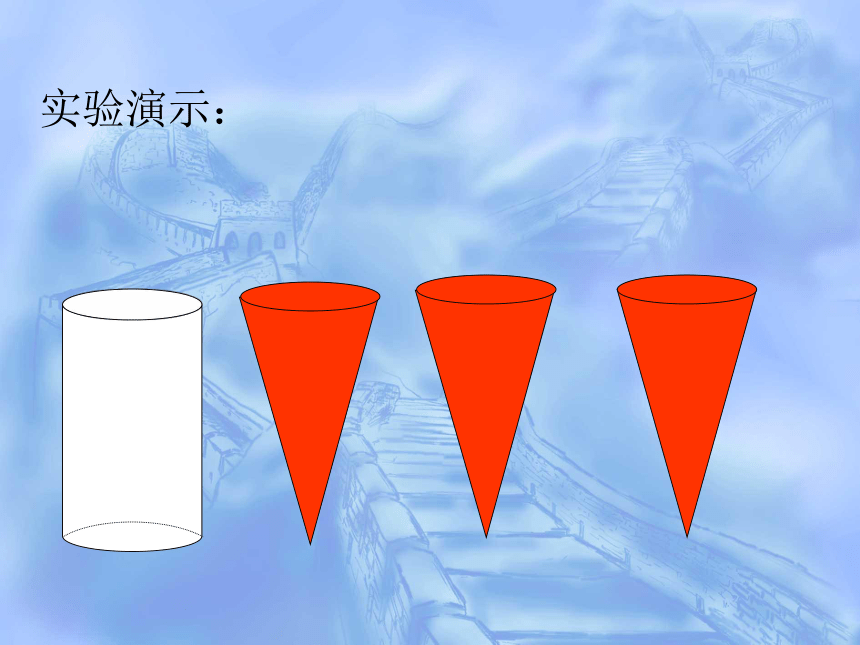
实验演示:
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
判断:
1、圆柱的体积是圆锥体积的3倍。(
)
2、圆锥的体积是和它等底等高圆柱体积的
(
)
3、正方体、长方体、圆锥体的体积都等于底面积×高.(
)
4、圆柱的体积大于和它等底等高的圆锥的体积(
)
√
√
×
×
根据已知条件求出圆锥的体积。
只列式不计算:
1、底面积3.14平方分米,高3分米。
2、底面半径3厘米,高5厘米。
3、底面直径10分米,高9分米。
4、底面周长12.56米,高4米。
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
填空:
1、圆锥的体积等于(
),用字母表示:(
)。
2、圆柱的体积等于和它(
)的圆锥的体积的(
)倍。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是
3立方分米,圆锥的体积是(
)立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
×底面积×高
等底等高
3
1
24
目标检测
判断:
1、圆柱体的体积一定比圆锥体的体积大(
)
2、圆锥的体积等于和它等底等高的圆柱体积的
。
(
)
3、圆锥的底面积是20平方厘米,高5厘米,体积是100立方厘米。(
)
4、一个圆柱体木料,把它加工成最大的圆锥体,削去的部分的体积和圆锥的体积比是2:1.
(
)
√
×
√
×
列式计算
1、求下面各圆锥的体积。(单位:厘米)
7
3
2.一堆圆锥形的煤体积是12立方米,底面积是6立方米,高是多少?
有一根底面直径是6厘米,长是10厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
10厘米
6厘米
3.14×(6÷2)×10×(1-
),
=3.14×9×10×
=188.4(立方厘米)
答:要削去钢材188.4立方厘米.
6÷2=3(厘米)
3.14
×3
×3×10=282.6(立方厘米)
282.6-282.6×
=188.4(立方厘米)
答:要削去钢材188.4立方厘米.
2
圆锥的体积
温故知新
1、圆柱的体积等于(
),用字母表示为(
)或(
)。
2、已知圆柱的体积和底面积,求高可以用公式(
)。
3、已知圆柱的体积和高,求表面积可以用公式(
)。
4、圆锥有什么特点?
h=v÷s
底面积×高
V=sh
V=兀r2h
s=v÷h
学习目标
长方体的体积=底面积×高
圆柱的体积
=
底面积×高
V
=
Sh
1、观察手中的实验工具,看看圆柱和圆锥的底面积和高有着怎样的关系?
2、利用手中的圆柱和圆锥学具探究二者之间体积的关系,并完成实验表格。
群学
–展示
学习提示
实验演示:
圆锥的体积V等于和它等底等高的圆柱体积的三分之一
判断:
1、圆柱的体积是圆锥体积的3倍。(
)
2、圆锥的体积是和它等底等高圆柱体积的
(
)
3、正方体、长方体、圆锥体的体积都等于底面积×高.(
)
4、圆柱的体积大于和它等底等高的圆锥的体积(
)
√
√
×
×
根据已知条件求出圆锥的体积。
只列式不计算:
1、底面积3.14平方分米,高3分米。
2、底面半径3厘米,高5厘米。
3、底面直径10分米,高9分米。
4、底面周长12.56米,高4米。
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
填空:
1、圆锥的体积等于(
),用字母表示:(
)。
2、圆柱的体积等于和它(
)的圆锥的体积的(
)倍。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是
3立方分米,圆锥的体积是(
)立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
×底面积×高
等底等高
3
1
24
目标检测
判断:
1、圆柱体的体积一定比圆锥体的体积大(
)
2、圆锥的体积等于和它等底等高的圆柱体积的
。
(
)
3、圆锥的底面积是20平方厘米,高5厘米,体积是100立方厘米。(
)
4、一个圆柱体木料,把它加工成最大的圆锥体,削去的部分的体积和圆锥的体积比是2:1.
(
)
√
×
√
×
列式计算
1、求下面各圆锥的体积。(单位:厘米)
7
3
2.一堆圆锥形的煤体积是12立方米,底面积是6立方米,高是多少?
有一根底面直径是6厘米,长是10厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
10厘米
6厘米
3.14×(6÷2)×10×(1-
),
=3.14×9×10×
=188.4(立方厘米)
答:要削去钢材188.4立方厘米.
6÷2=3(厘米)
3.14
×3
×3×10=282.6(立方厘米)
282.6-282.6×
=188.4(立方厘米)
答:要削去钢材188.4立方厘米.
2
