探究弹性势能的表达式
图片预览




文档简介
(共19张PPT)
观察
两张图中的物体有什么共同点?
5.5 探究弹性势能的表达式
1.弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
2.猜想:猜猜猜
弹簧的弹性势能可能与哪些物理量有关?
k一定,Δk越大,弹性势能越大
Δl一定,k越大,弹性势能越大
与弹簧的伸长量Δl,
劲度系数k有关
2.猜想:猜猜猜
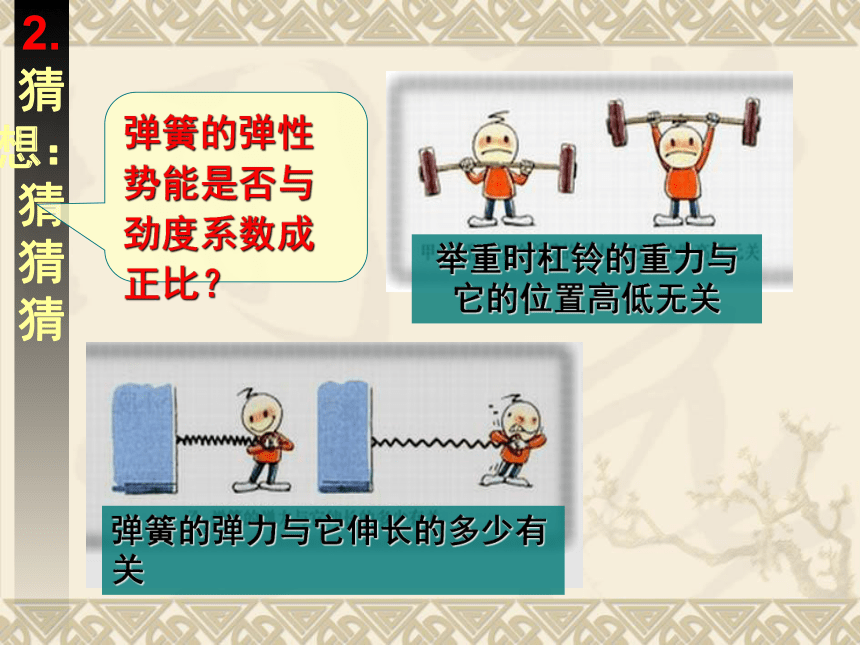
弹簧的弹性势能是否与劲度系数成正比?
举重时杠铃的重力与它的位置高低无关
弹簧的弹力与它伸长的多少有关
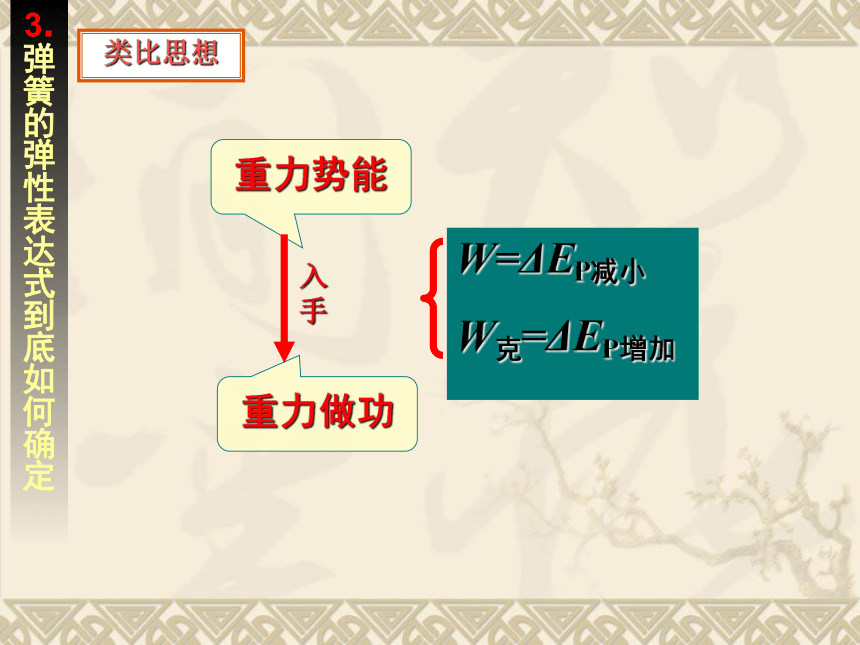
3.弹 簧 的弹性表达式到底如何确定
重力势能
重力做功
入手
W=ΔEP减小
W克=ΔEP增加
类比思想
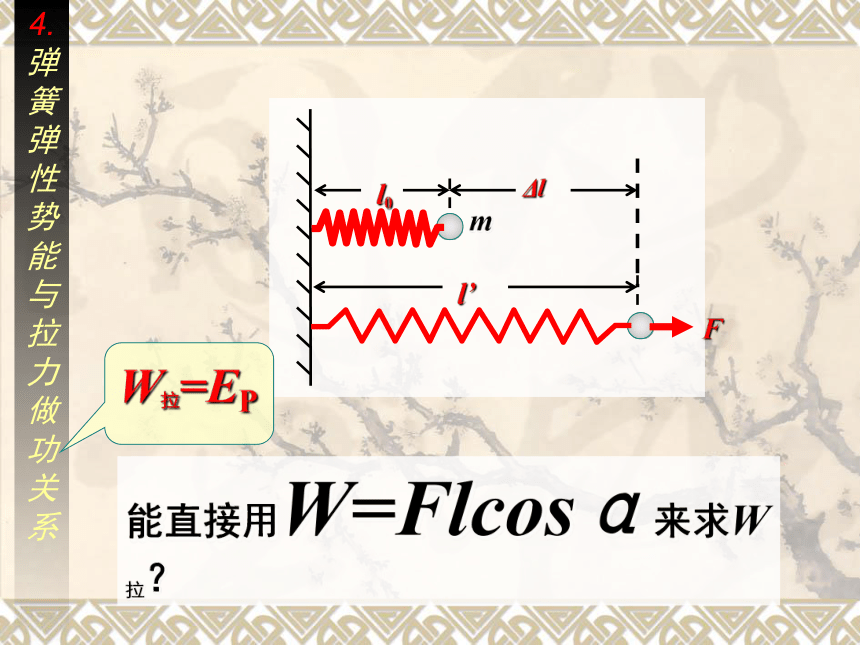
4.弹簧弹性势能与拉力做功关系
能直接用W=Flcosα来求W拉?
l’
Δl
l0
m
F
W拉=EP
5.怎样计算拉力做所做的功?
在各个小段上,弹力可近似认为是不变的
把弹簧从A到B的过程分成很多小段
Δl1,Δl2,Δl3…
F1、F2、F3 …
W=F1Δl1+F2Δl2+F3Δl3+…
积分
思想
微分
思想
匀速直线运动与匀变速直线运动位移的计算。
知识回放
1. 匀速直线运动的位移
1. 匀速直线运动的位移
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
o
F
o
Δl
F
o
Δl
F
6.怎样计算这个求和式?
每段拉力做的功就可用图中细窄的矩形面积表示,对这些矩形面积求和,就得到了有F和Δl围成的三角形面积,这块三角形的面积就表示拉力在整个过程中所做的功。
Δl
Δl
kΔl
Δl
7.弹性势能的表达式
EP=kΔl2/2
k为弹簧的劲度系数
Δl为弹簧的伸长或缩短量
如图所示,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下物体处于静止状态。当撤去F后,物体将向右运动,在物体向右运动过程中下列说法正确的是: A、弹簧的弹性势能逐渐减小
B、弹簧的弹性势能逐渐增大
C、弹簧的弹性势能先增大再减小
D、弹簧的弹性势能先减小再增大
练习
单项
B
F
观察
两张图中的物体有什么共同点?
5.5 探究弹性势能的表达式
1.弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
2.猜想:猜猜猜
弹簧的弹性势能可能与哪些物理量有关?
k一定,Δk越大,弹性势能越大
Δl一定,k越大,弹性势能越大
与弹簧的伸长量Δl,
劲度系数k有关
2.猜想:猜猜猜
弹簧的弹性势能是否与劲度系数成正比?
举重时杠铃的重力与它的位置高低无关
弹簧的弹力与它伸长的多少有关
3.弹 簧 的弹性表达式到底如何确定
重力势能
重力做功
入手
W=ΔEP减小
W克=ΔEP增加
类比思想
4.弹簧弹性势能与拉力做功关系
能直接用W=Flcosα来求W拉?
l’
Δl
l0
m
F
W拉=EP
5.怎样计算拉力做所做的功?
在各个小段上,弹力可近似认为是不变的
把弹簧从A到B的过程分成很多小段
Δl1,Δl2,Δl3…
F1、F2、F3 …
W=F1Δl1+F2Δl2+F3Δl3+…
积分
思想
微分
思想
匀速直线运动与匀变速直线运动位移的计算。
知识回放
1. 匀速直线运动的位移
1. 匀速直线运动的位移
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
2. 怎么求匀变速直线运动的位移?
o
F
o
Δl
F
o
Δl
F
6.怎样计算这个求和式?
每段拉力做的功就可用图中细窄的矩形面积表示,对这些矩形面积求和,就得到了有F和Δl围成的三角形面积,这块三角形的面积就表示拉力在整个过程中所做的功。
Δl
Δl
kΔl
Δl
7.弹性势能的表达式
EP=kΔl2/2
k为弹簧的劲度系数
Δl为弹簧的伸长或缩短量
如图所示,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下物体处于静止状态。当撤去F后,物体将向右运动,在物体向右运动过程中下列说法正确的是: A、弹簧的弹性势能逐渐减小
B、弹簧的弹性势能逐渐增大
C、弹簧的弹性势能先增大再减小
D、弹簧的弹性势能先减小再增大
练习
单项
B
F
