第一章碰撞与动量守恒第3节动量守恒定律的应用(1)课件(共22张PPT)
文档属性
| 名称 | 第一章碰撞与动量守恒第3节动量守恒定律的应用(1)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-26 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
动量守恒定律
公式
内容
应用对象
动量守恒条件
如果系统不受外力,或所受外力的矢量和为零,这个系统的动量就保持不变。
系
统
不受外力或合外力为零;
外力远小于系统内力;
某方向不受外力或合外力为零
复习
应用动量守恒定律解题的一般步骤
1、明确研究对象(系统包括哪几个物体及其运动过程);
2、进行受力分析、判断系统动量是否守恒(或某一方向是否守恒);
3、规定正方向,确定初末状态的动量;
4、由动量守恒定律列方程求解;
5、必要时进行讨论。
第3节
动量守恒定律的典型应用
1)碰撞时间极短
2)碰撞内力很大,外力可以忽略不计,系统动量守恒
1、碰撞特点
一、碰撞模型
2、遵循规律
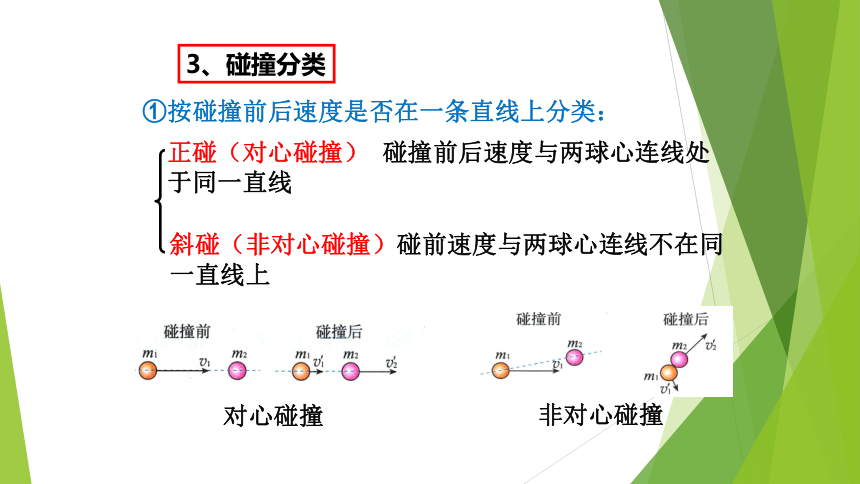
正碰(对心碰撞)
碰撞前后速度与两球心连线处
于同一直线
斜碰(非对心碰撞)碰前速度与两球心连线不在同一直线上
①按碰撞前后速度是否在一条直线上分类:
3、碰撞分类
对心碰撞
非对心碰撞
3、碰撞分类
②碰撞前后两物体总动能是否变化
完全弹性碰撞
A
B
B
B
A
A
v1
v2=0
F1
F2
光滑水平面上,有两个小球A和B,质量分别为m1和m2,
B球静止,A以球速度v1和B球发生弹性正碰,求:碰后两球的速度v1’和v2’。
动量守恒
设置情境
机械能守恒
V1
V2=0
光滑
若
m1
>>
m2
1.等质量碰撞:
2.“大”碰“小”
交换速度
跟着跑
v1’=0
,v2’=v1
v1’>0
,v2’>0
v1’=
v1,v2’=2v1
“中子的发现”教材
P12
,P14
发展空间
若
m2
>>
m1
3.“小”碰“大”
要反向
v1’<0
,v2’>0
v1’=
-v1
,
v2’=0
要反弹
思考
若两小球发射非弹性正碰,什么情况下系统机械能损失最大呢?
非完全弹性碰撞
3、碰撞分类
②按动能是否损失分类:
完全弹性碰撞
非完全弹性碰撞
完全非弹性碰撞
1.
在光滑水平面上,动能为
E0
,动量大小为
p0
的小球
1
与静止的小球
2
发生碰撞,碰撞前后球
1
的运动方向相反,将碰后球
1
的动能和动量大小分别记为
E1、p1,球
2
的动能和动量大小分别记为
E2、p2,则必有
(碰后两球速度不为零)(
)
A.
E1
<
E0
B.
p1
<
p0
C.
E2
>
E0
D.
p2
>
p0
解析:碰撞过程中两球的总动能不会增加,则:
否则就违反了能量守恒,故A、B正确,C错误;
由动量守恒得:
得到:
故,D正确。
应用1、碰撞后物体可能的运动状态问题
碰撞结果可能有各种可能,但不管哪种结果必须满足以下三条:
(1)系统动量守恒,即p1+p2=p1′+p2′
(2)系统的总动能不增加,即Ek前
≥
Ek后
(3)速度要合理性(正碰)
①若碰前同向运动
,则碰前v入射>v被碰;
碰后仍同向运动,则原来在前的物体速度一定增大,即v前≥v后
②若碰后有物体静止,则一定是碰前动量大的物体停下来.
例:质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动,A球的动量pA=9
kg·m/s,B球的动量pB=3
kg·m/s,当A球追上B球时发生碰撞,则碰撞后A、B两球动量的可能值是( )
A.pA′=6
kg·m/s,pB′=6
kg·m/s
B.pA′=8
kg·m/s,pB′=4
kg·m/s
C.pA′=-2
kg·m/s,pB′=14
kg·m/s
D.pA′=-4
kg·m/s,pB′=17
kg·m/s
法宝1:三个判据
????????(1)动量守恒
????????(2)动能不增
?????(3)速度合理
法宝2:极限分析—
可能性介于弹性碰撞与完全非弹性碰撞之间的状态。
????????若不明确碰撞形变的恢复程度,则碰后两物体速度可能的取值应在弹性碰撞后的速度与完全非弹性碰撞后的速度的取值之间。
碰撞后物体可能运动状态问题的分析
碰撞过程中能量与形变量的演变——碰撞过程的“慢镜头”
v1
v共
弹性碰撞
非弹性碰撞
完全非弹性碰撞
3.甲、乙两球在水平光滑轨道上向同方向运动,已知它们的动量分别是p1=5
kg·m/s,p2=7
kg·m/s,甲从后面追上乙并发生碰撞,碰后乙球的动量变为10
kg·m/s,则两球质量m1与m2间的关系可能是( )
A.m1=m2
B.2m1=m2
C.4m1=m2
D.6m1=m2
2、类碰撞模型
解析:选C 甲、乙两球在碰撞过程中动量守恒,
所以有p1+p2=p1′+p2′,得p1′=2
kg·m/s。
由于在碰撞过程中,系统的机械能不会增加。所以有
,得m1≤m2。因为题目给出物
理情景是“甲从后面追上乙”,要符合这一物理情
景,就必须有,即m1同时还要符合碰撞后乙球的速度必须大于或等于甲
球的速度这一物理情景,
即,所以m1≥m2。因此选项C正确。
动量守恒定律
公式
内容
应用对象
动量守恒条件
如果系统不受外力,或所受外力的矢量和为零,这个系统的动量就保持不变。
系
统
不受外力或合外力为零;
外力远小于系统内力;
某方向不受外力或合外力为零
复习
应用动量守恒定律解题的一般步骤
1、明确研究对象(系统包括哪几个物体及其运动过程);
2、进行受力分析、判断系统动量是否守恒(或某一方向是否守恒);
3、规定正方向,确定初末状态的动量;
4、由动量守恒定律列方程求解;
5、必要时进行讨论。
第3节
动量守恒定律的典型应用
1)碰撞时间极短
2)碰撞内力很大,外力可以忽略不计,系统动量守恒
1、碰撞特点
一、碰撞模型
2、遵循规律
正碰(对心碰撞)
碰撞前后速度与两球心连线处
于同一直线
斜碰(非对心碰撞)碰前速度与两球心连线不在同一直线上
①按碰撞前后速度是否在一条直线上分类:
3、碰撞分类
对心碰撞
非对心碰撞
3、碰撞分类
②碰撞前后两物体总动能是否变化
完全弹性碰撞
A
B
B
B
A
A
v1
v2=0
F1
F2
光滑水平面上,有两个小球A和B,质量分别为m1和m2,
B球静止,A以球速度v1和B球发生弹性正碰,求:碰后两球的速度v1’和v2’。
动量守恒
设置情境
机械能守恒
V1
V2=0
光滑
若
m1
>>
m2
1.等质量碰撞:
2.“大”碰“小”
交换速度
跟着跑
v1’=0
,v2’=v1
v1’>0
,v2’>0
v1’=
v1,v2’=2v1
“中子的发现”教材
P12
,P14
发展空间
若
m2
>>
m1
3.“小”碰“大”
要反向
v1’<0
,v2’>0
v1’=
-v1
,
v2’=0
要反弹
思考
若两小球发射非弹性正碰,什么情况下系统机械能损失最大呢?
非完全弹性碰撞
3、碰撞分类
②按动能是否损失分类:
完全弹性碰撞
非完全弹性碰撞
完全非弹性碰撞
1.
在光滑水平面上,动能为
E0
,动量大小为
p0
的小球
1
与静止的小球
2
发生碰撞,碰撞前后球
1
的运动方向相反,将碰后球
1
的动能和动量大小分别记为
E1、p1,球
2
的动能和动量大小分别记为
E2、p2,则必有
(碰后两球速度不为零)(
)
A.
E1
<
E0
B.
p1
<
p0
C.
E2
>
E0
D.
p2
>
p0
解析:碰撞过程中两球的总动能不会增加,则:
否则就违反了能量守恒,故A、B正确,C错误;
由动量守恒得:
得到:
故,D正确。
应用1、碰撞后物体可能的运动状态问题
碰撞结果可能有各种可能,但不管哪种结果必须满足以下三条:
(1)系统动量守恒,即p1+p2=p1′+p2′
(2)系统的总动能不增加,即Ek前
≥
Ek后
(3)速度要合理性(正碰)
①若碰前同向运动
,则碰前v入射>v被碰;
碰后仍同向运动,则原来在前的物体速度一定增大,即v前≥v后
②若碰后有物体静止,则一定是碰前动量大的物体停下来.
例:质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动,A球的动量pA=9
kg·m/s,B球的动量pB=3
kg·m/s,当A球追上B球时发生碰撞,则碰撞后A、B两球动量的可能值是( )
A.pA′=6
kg·m/s,pB′=6
kg·m/s
B.pA′=8
kg·m/s,pB′=4
kg·m/s
C.pA′=-2
kg·m/s,pB′=14
kg·m/s
D.pA′=-4
kg·m/s,pB′=17
kg·m/s
法宝1:三个判据
????????(1)动量守恒
????????(2)动能不增
?????(3)速度合理
法宝2:极限分析—
可能性介于弹性碰撞与完全非弹性碰撞之间的状态。
????????若不明确碰撞形变的恢复程度,则碰后两物体速度可能的取值应在弹性碰撞后的速度与完全非弹性碰撞后的速度的取值之间。
碰撞后物体可能运动状态问题的分析
碰撞过程中能量与形变量的演变——碰撞过程的“慢镜头”
v1
v共
弹性碰撞
非弹性碰撞
完全非弹性碰撞
3.甲、乙两球在水平光滑轨道上向同方向运动,已知它们的动量分别是p1=5
kg·m/s,p2=7
kg·m/s,甲从后面追上乙并发生碰撞,碰后乙球的动量变为10
kg·m/s,则两球质量m1与m2间的关系可能是( )
A.m1=m2
B.2m1=m2
C.4m1=m2
D.6m1=m2
2、类碰撞模型
解析:选C 甲、乙两球在碰撞过程中动量守恒,
所以有p1+p2=p1′+p2′,得p1′=2
kg·m/s。
由于在碰撞过程中,系统的机械能不会增加。所以有
,得m1≤m2。因为题目给出物
理情景是“甲从后面追上乙”,要符合这一物理情
景,就必须有,即m1
球的速度这一物理情景,
即,所以m1≥m2。因此选项C正确。
