苏科版七下数学9.4乘法公式教案

《平方差公式》教学设计
教学目标：1、经历平方差公式的探索过程，进一步发展学生的符号感和推理能力、归纳能力；
2、掌握平方差公式的结构特征，能运用公式进行简单的运算；
3、会用几何图形说明公式的意义，体会数形结合的思想方法.
教学重点：1、
学会平方差公式的推导和应用
2、
理解和掌握平方差公式，并能灵活运用公式进行简单运算。
教学难点：能灵活运用公式进行运算.
教学课时：一课时
教学过程
复习回顾：复习多项式乘法法则
提问：（a+b）（m+n）=_____
举例：计算（x
＋
2)(
x＋5）
创设情境，导入新课
问题：王剑同学去商店买了单价是9.8元／千克的糖块10.2千克，售货员刚拿起计算器，王剑就说出应付99.96元，结果与售货员计算出的结果相同。售货员惊讶地问：“这位同学，你怎么算得这么快?”王剑同学说：“我利用了数学课上刚学过的一个公式。”你知道王剑同学用的是什么数学公式吗?学了本节之后，你就能解决这个问题了.
探索新知，尝试发现
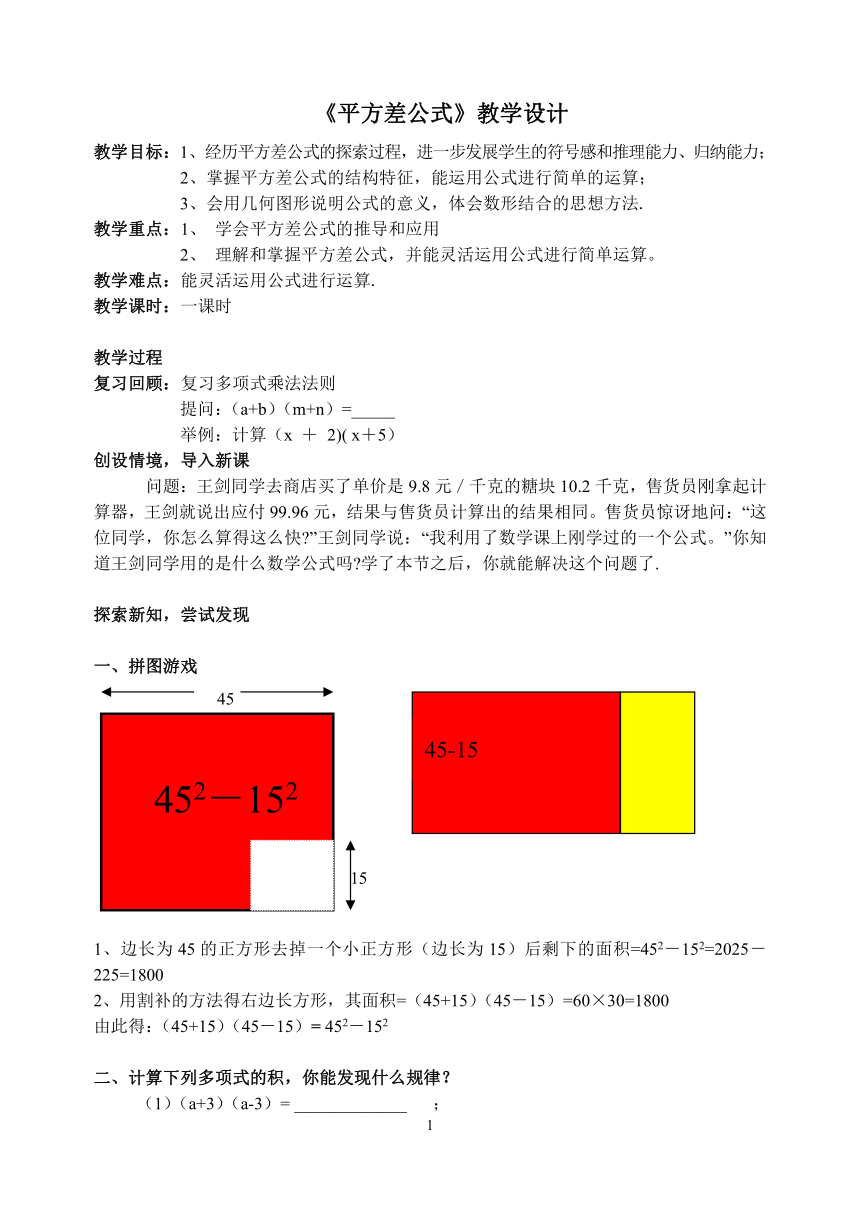
一、拼图游戏
1、边长为45的正方形去掉一个小正方形（边长为15）后剩下的面积=452－152=2025－225=1800
2、用割补的方法得右边长方形，其面积=（45+15）（45－15）=60×30=1800
由此得：（45+15）（45－15）=
452－152
二、计算下列多项式的积，你能发现什么规律？
（1）（a+3）（a-3）=
_____________??????；?
（2）（n+
m）（n-
m）=____________
???；
（3）（2x+3）（2x-3）=____________
????????．
依照以上三道题的计算回答下列问题：
?
?①式子的左边具有什么共同特征？
②它们的结果有什么特征？
?
?③能不能用字母表示你的发现？
教师提问，学生通过自主探究、合作交流，发现规律，式子左边是两个数的和与这两个数的差的积，右边是这两个数的平方差，并猜想出：（a+b）（a-
b）=a?-
b?．?　　
三、总结归纳，发现规律
你能用文字语言表示所发现的规律吗？
两个数的和与这两个数的差的积，等于这两个数的平方差．?
四、剖析公式，发现本质?
在平方差公式中，其结构特征为：（a+b）（a-
b）=a?-
b?
(1)
公式左边两个二项式必须是相同两数的和与差相乘；且左边两括号内的第一项相等、第二项符号相反[互为相反数(式)];
(2)
公式右边是这两个数的平方差；即右边是左边括号内第一项的平方减去第二项的平方.
(3)
公式中的
a和b
可以代表数，也可以是代数式．
五、巩固运用，内化新知
例1
利用平方差公式计算：
（1）(5+6x)(5?6x)；
(2)
(x+2y)(2y?x);
(3)
(?a+2b)(?a?2b).
解:
(1)(5+6x)(5?6x)
(2)
(x+2y)(2y?x)
(3)(?a+2b)(?a?2b)
=5
?－（6x）?
=(2y+x)(2y－x)
=(-a)
?－(2b)
?
=25－36x
?
=(2y)
?－x?
=a?－4b?
=4y?－x?
注意：当“第一(二)数”是一分数或是数与字母的乘积时,
要用括号把这个数整个括起来，最后的结果又要去掉括号。
情系中考
1、【上海】（a-2b）（a+2b）=____________
2、【宁夏】（x-y）（-y-x）的结果是（
）
A.-x?+y?
B.-x?-y?
C.x?-y?
D.x?+y?
例2
利用平方差公式计算：102×98
解:
102×98
=
(100
+2)
×(100-2
)
=1002
?22
=10000
?
4
=9996
利用例2的方法解决引人中的问题，揭露王剑同学算的又快又准的奥秘。
随堂练习，巩固所学
计算：
(1)(a+2)(a?2)
(2)51×49
(3)(?2x+y)(2x+y)
(4)(x?y)(?x?y)
例3
计算(a＋b+c)(a－b+c)
提示：将(a＋c)看着整体，转化为[(a＋c)
＋b]
[(a＋c)
－b]
，再利用平方差公式进行计算
课堂小结(学生总结)：
本节课你学到了什么？
1、平方差公式
两个数的和与这两个数的差的积等于这两个数的平方差．这个公式叫做乘法的平方差公式．即(a+b)(a?b)=a??b?
2、公式的结构特征
①公式的字母a、b可以表示数，也可以表示单项式、多项式；
②要符合公式的结构特征才能运用平方差公式。
3、运用平方差公式的步骤：先比形式，再套公式
作业：1.
(2x－1)(2x＋1)(4x2＋1)
2.
(2+1)(22+1)(24+1)(28+1)(216+1)+1
45+15
45
15
4545
452－152
45-15
15
PAGE
2