2020中考数学一轮复习锐角三角函数知识点及考点梳理学案
文档属性
| 名称 | 2020中考数学一轮复习锐角三角函数知识点及考点梳理学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 703.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-26 00:00:00 | ||
图片预览


文档简介
中考复习—《三角函数》知识点及考点梳理
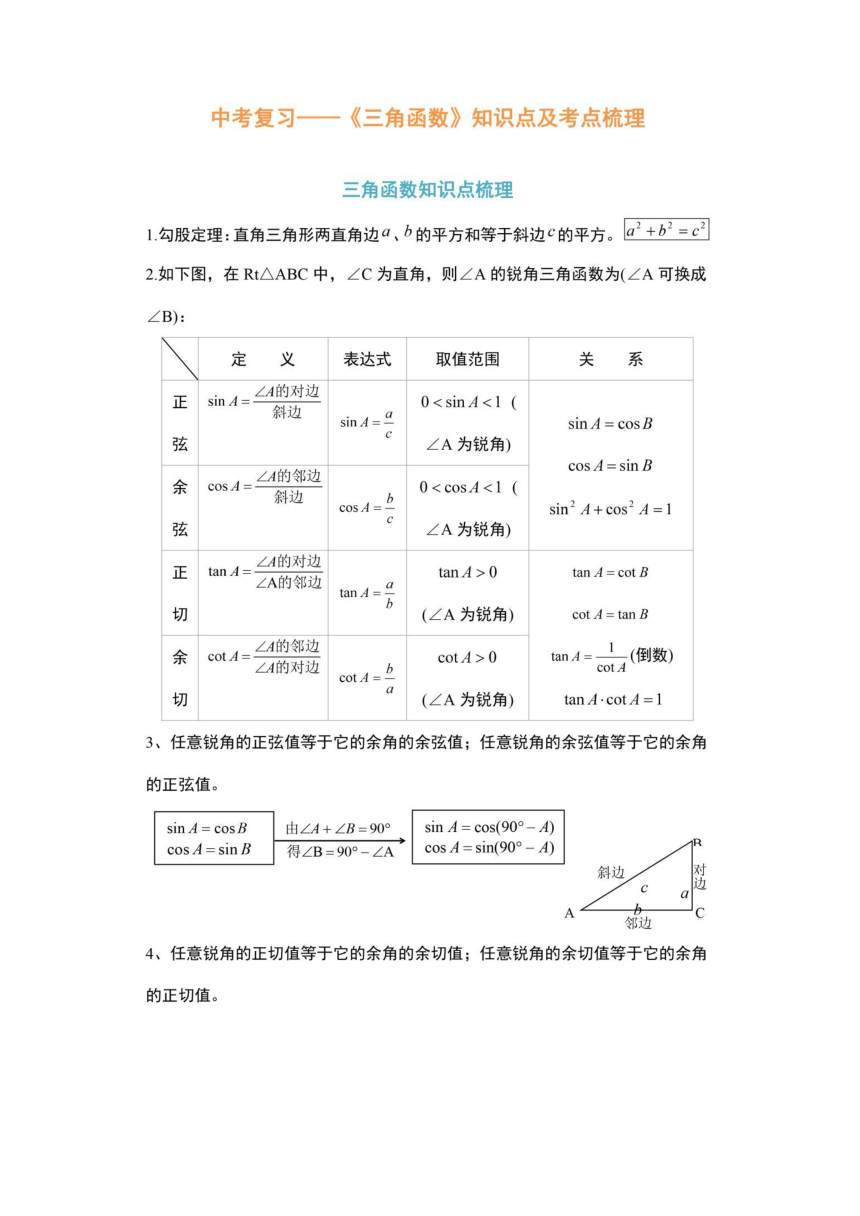
三角函数知识点梳理
1勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。口2+b2=c2
2如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成
∠B):
定义
表达式
取值范围
关系
∠A的对边
正sinA
斜边
0A
<1
sin
a=
sin
a=
cos
B
弦
∠A为锐角)
cos
A=sin
B
余
∠A的邻边
斜边
b
0cOS
A
sin
a+cos
A=1
弦
∠A为锐角)
∠A的对边
正tanA
∠A的邻边
tana>o
tan
a=cot
B
tan
g-_a
(∠A为锐角)
cot
a=
tan
B
余cotA
∠A的邻边
cot
a>o
tan
a
(倒数)
∠A的对边
cot
a
切
(∠A为锐角)
tanA·cotA=1
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角
的正弦值。
sinA=cosB由∠A+∠B=90°sinA=cos(90°-A)
cosA=sinB「得∠B=90°∠
A
COS
A=sin(900-A)
斜边
A
C
邻边
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角
的正切值。
由∠A+∠B=90°
tan
A=
cot
B
得∠B=90°-∠A,
tan
A=cot(90-A)
cot
A=tan
B
cotA=tan(90°-A)
50°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数0°
30
45°
60°
90
sin
a
2
0
2
tan
a
cot
a
6正弦、余弦的增减性:当0α∞90°时,sinα随α的增大而增大,cosα随α的
增大而减小
7正切、余切的增减性:当0α<90°时,tan∝随∝的增大而增大,cotc随∝的
增大而减小。
8解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和
角
依据:①边的关系:a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函
数的定义。(注意:尽量避免使用中间数据和除法)
9应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角
视线
铅垂线
4仰角水平线
俯角
h
h:l
视线
(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。用字母表示,即i
三角函数知识点梳理
1勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。口2+b2=c2
2如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成
∠B):
定义
表达式
取值范围
关系
∠A的对边
正sinA
斜边
0
<1
sin
a=
sin
a=
cos
B
弦
∠A为锐角)
cos
A=sin
B
余
∠A的邻边
斜边
b
0
A
sin
a+cos
A=1
弦
∠A为锐角)
∠A的对边
正tanA
∠A的邻边
tana>o
tan
a=cot
B
tan
g-_a
(∠A为锐角)
cot
a=
tan
B
余cotA
∠A的邻边
cot
a>o
tan
a
(倒数)
∠A的对边
cot
a
切
(∠A为锐角)
tanA·cotA=1
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角
的正弦值。
sinA=cosB由∠A+∠B=90°sinA=cos(90°-A)
cosA=sinB「得∠B=90°∠
A
COS
A=sin(900-A)
斜边
A
C
邻边
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角
的正切值。
由∠A+∠B=90°
tan
A=
cot
B
得∠B=90°-∠A,
tan
A=cot(90-A)
cot
A=tan
B
cotA=tan(90°-A)
50°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数0°
30
45°
60°
90
sin
a
2
0
2
tan
a
cot
a
6正弦、余弦的增减性:当0α∞90°时,sinα随α的增大而增大,cosα随α的
增大而减小
7正切、余切的增减性:当0α<90°时,tan∝随∝的增大而增大,cotc随∝的
增大而减小。
8解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和
角
依据:①边的关系:a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函
数的定义。(注意:尽量避免使用中间数据和除法)
9应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角
视线
铅垂线
4仰角水平线
俯角
h
h:l
视线
(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。用字母表示,即i
同课章节目录
