全等判定ASA
图片预览



文档简介
(共15张PPT)
全等三角形的判定
坦洲实验中学数学组
新 授 课
ASA
1.什么是全等三角形?
2.判定两个三角形全等要具备什么条件
边边边:三边对应相等的两个三角形全等。
边角边:有两边和它们夹角对应相等的两
个三角形全等。
回顾与思考
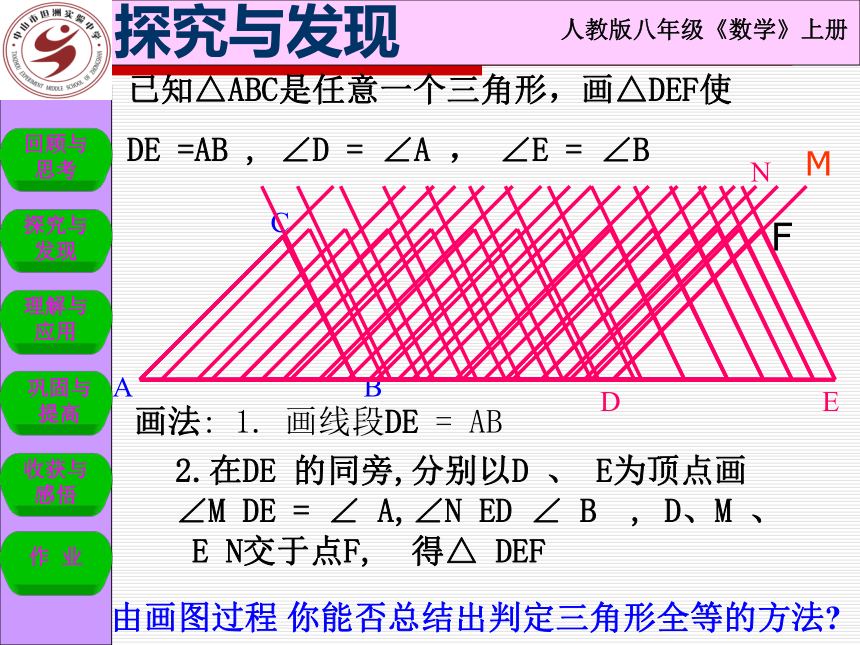
已知△ABC是任意一个三角形,画△DEF使
DE =AB , ∠D = ∠A , ∠E = ∠B
A
C
B
D
E
N
画法: 1. 画线段DE = AB
2.在DE 的同旁,分别以D 、 E为顶点画
∠M DE = ∠ A,∠N ED ∠ B , D、M 、
E N交于点F, 得△ DEF
由画图过程 你能否总结出判定三角形全等的方法
M
F
探究与发现
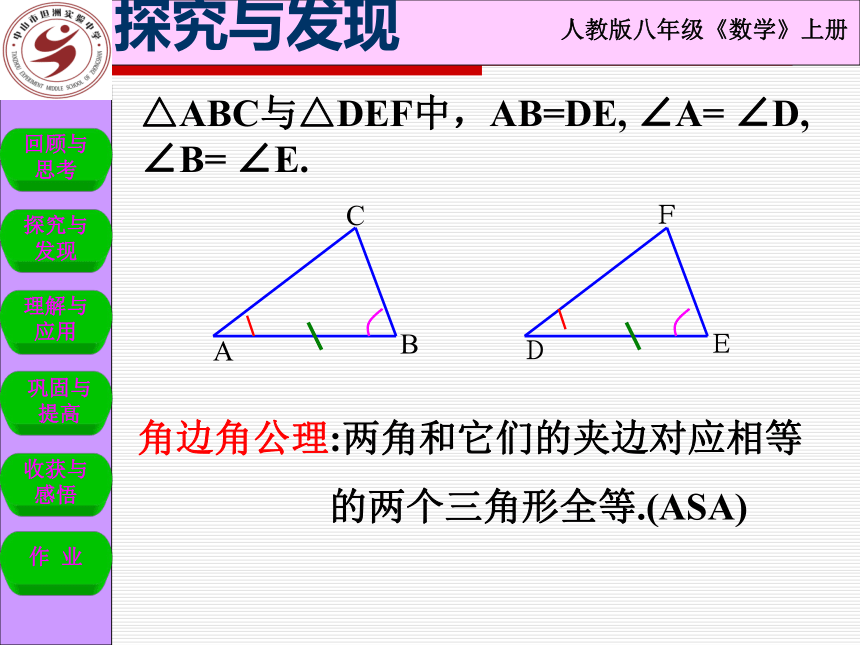
△ABC与△DEF中,AB=DE, ∠A= ∠D, ∠B= ∠E.
C
A
B
角边角公理:两角和它们的夹边对应相等
的两个三角形全等.(ASA)
探究与发现
F
D
E
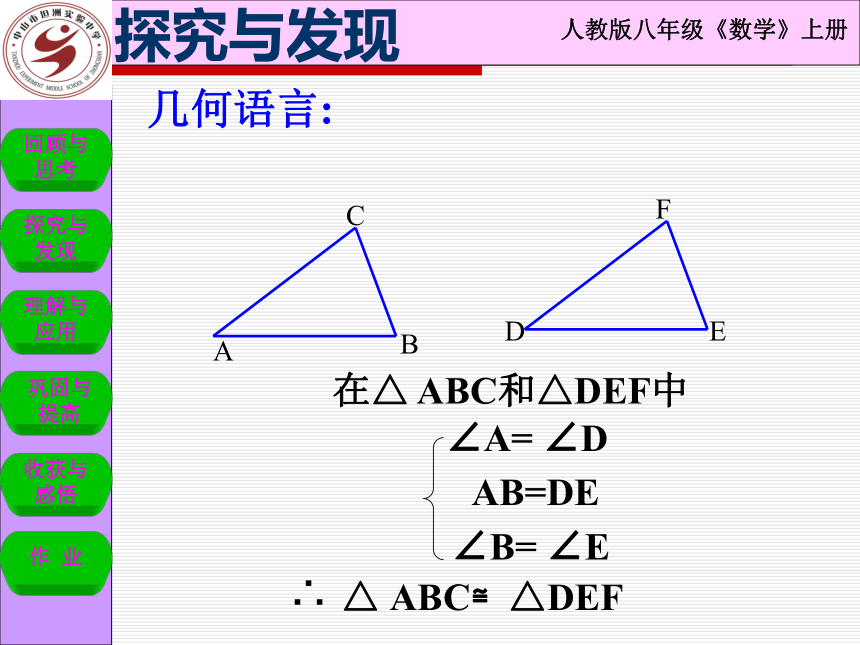
在△ ABC和△DEF中
△ ABC≌△DEF
∠A= ∠D
AB=DE
∠B= ∠E
∴
几何语言:
探究与发现
C
A
B
E
D
F
例已知:如图,点B,F,C,E在同一条直线,FB=CE,AB∥ED,AC∥FD,
求证:AB=DE,AC=DF
D
C
B
A
E
F
证明:∵FB=CE(已知)
FC=FC
∴BC=EF
∵AB∥ED,AC∥FD(已知)
∴∠B=∠E,∠ACB=∠DFE
在△ABC与△DEF中
{
BC=EF(已证)
∠B=∠E(已证)
∠ACB=∠DFE(已证)
∴△ABC≌△DEF(ASA)
∴AB=DE,AC=DF
理解与应用
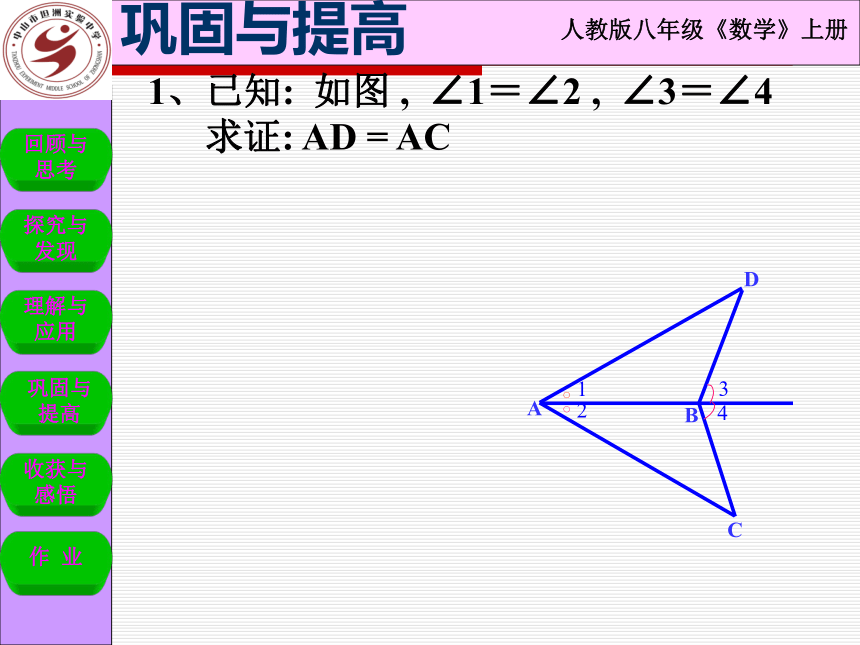
1、已知: 如图 , ∠1=∠2 , ∠3=∠4
求证: AD = AC
A
D
C
B
3
4
○
○
1
2
巩固与提高
证明:在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴△ABD≌△ACE (ASA)
已知:AB=AC,∠B=∠C,
求证:△ABD≌△ACE
A
B
D
C
E
练习1:
已知:B E C F 在同一直线上,AB ∥DE
AC∥DF, BE=CF, 求证: △ABC≌ △DEF
证明: ∵AB ∥DE
在△ABC和△DEF中
∠B=∠DEF
BE=CF
∠F=∠ACB
∵ BE=CF EC=EC
∴ BC=EF
△ ABC≌ △ DEF
∴∠B=∠DEF
∵ AC∥DF
∴∠F=∠ACB
全等三角形的判定方法
边边边
SSS 三边对应相等的两个三角形全等.
边角边
SAS 有两边和它们的夹角对应
相等的两个三角形全等.
角边角
ASA 有两角和它们的夹边对应
相等的两个三角形全等.
收获与感悟
收获与感悟
怎么办?可以帮帮我吗?
一张教学用的三角形硬纸板不小心被撕坏了,
如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
C
B
E
A
D
应用
如图,已知AB=BC,AB⊥BC,AD ⊥DE于D,
CE ⊥DE于E,求证:DB=EC
l
2
C
A
D
B
E
谢谢合作,
再见!
全等三角形的判定
坦洲实验中学数学组
新 授 课
ASA
1.什么是全等三角形?
2.判定两个三角形全等要具备什么条件
边边边:三边对应相等的两个三角形全等。
边角边:有两边和它们夹角对应相等的两
个三角形全等。
回顾与思考
已知△ABC是任意一个三角形,画△DEF使
DE =AB , ∠D = ∠A , ∠E = ∠B
A
C
B
D
E
N
画法: 1. 画线段DE = AB
2.在DE 的同旁,分别以D 、 E为顶点画
∠M DE = ∠ A,∠N ED ∠ B , D、M 、
E N交于点F, 得△ DEF
由画图过程 你能否总结出判定三角形全等的方法
M
F
探究与发现
△ABC与△DEF中,AB=DE, ∠A= ∠D, ∠B= ∠E.
C
A
B
角边角公理:两角和它们的夹边对应相等
的两个三角形全等.(ASA)
探究与发现
F
D
E
在△ ABC和△DEF中
△ ABC≌△DEF
∠A= ∠D
AB=DE
∠B= ∠E
∴
几何语言:
探究与发现
C
A
B
E
D
F
例已知:如图,点B,F,C,E在同一条直线,FB=CE,AB∥ED,AC∥FD,
求证:AB=DE,AC=DF
D
C
B
A
E
F
证明:∵FB=CE(已知)
FC=FC
∴BC=EF
∵AB∥ED,AC∥FD(已知)
∴∠B=∠E,∠ACB=∠DFE
在△ABC与△DEF中
{
BC=EF(已证)
∠B=∠E(已证)
∠ACB=∠DFE(已证)
∴△ABC≌△DEF(ASA)
∴AB=DE,AC=DF
理解与应用
1、已知: 如图 , ∠1=∠2 , ∠3=∠4
求证: AD = AC
A
D
C
B
3
4
○
○
1
2
巩固与提高
证明:在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC (已知)
∠A=∠A(公共角)
∴△ABD≌△ACE (ASA)
已知:AB=AC,∠B=∠C,
求证:△ABD≌△ACE
A
B
D
C
E
练习1:
已知:B E C F 在同一直线上,AB ∥DE
AC∥DF, BE=CF, 求证: △ABC≌ △DEF
证明: ∵AB ∥DE
在△ABC和△DEF中
∠B=∠DEF
BE=CF
∠F=∠ACB
∵ BE=CF EC=EC
∴ BC=EF
△ ABC≌ △ DEF
∴∠B=∠DEF
∵ AC∥DF
∴∠F=∠ACB
全等三角形的判定方法
边边边
SSS 三边对应相等的两个三角形全等.
边角边
SAS 有两边和它们的夹角对应
相等的两个三角形全等.
角边角
ASA 有两角和它们的夹边对应
相等的两个三角形全等.
收获与感悟
收获与感悟
怎么办?可以帮帮我吗?
一张教学用的三角形硬纸板不小心被撕坏了,
如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
C
B
E
A
D
应用
如图,已知AB=BC,AB⊥BC,AD ⊥DE于D,
CE ⊥DE于E,求证:DB=EC
l
2
C
A
D
B
E
谢谢合作,
再见!
