应用举例
图片预览







文档简介
(共23张PPT)
应用举例
应用举例
测量距离
解三角形模块
探究1.如图, 设A、B两点在河的两岸, 要测量两点之间的距离, 测量者在A的同侧, 在所在的河岸边选定一点C, 测出AC的距离是42m, ∠BAC=45 , ∠ACB=75 , 求 AB的长.
C
A
B
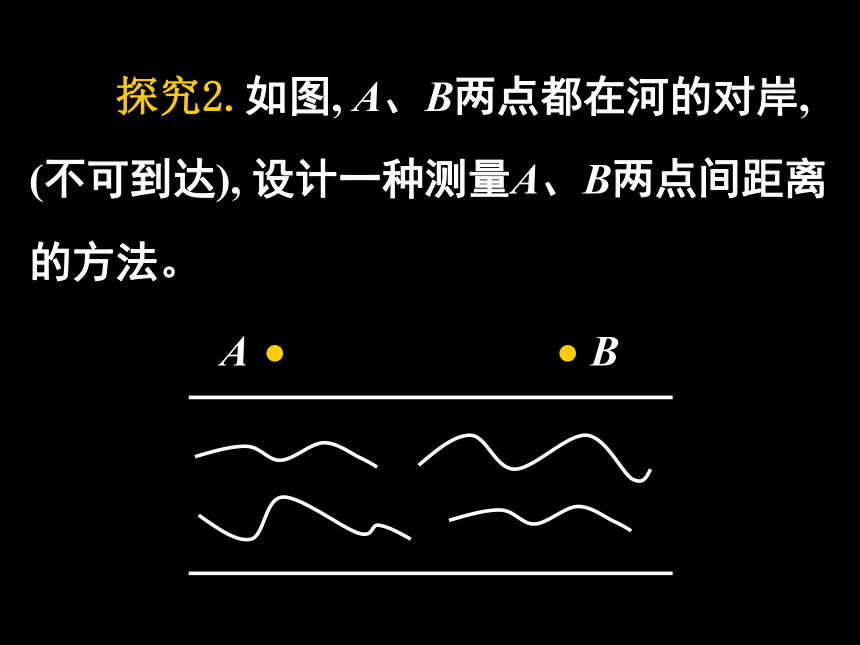
探究2.如图, A、B两点都在河的对岸, (不可到达), 设计一种测量A、B两点间距离的方法。
A
B
教材P13练习 T1、T2
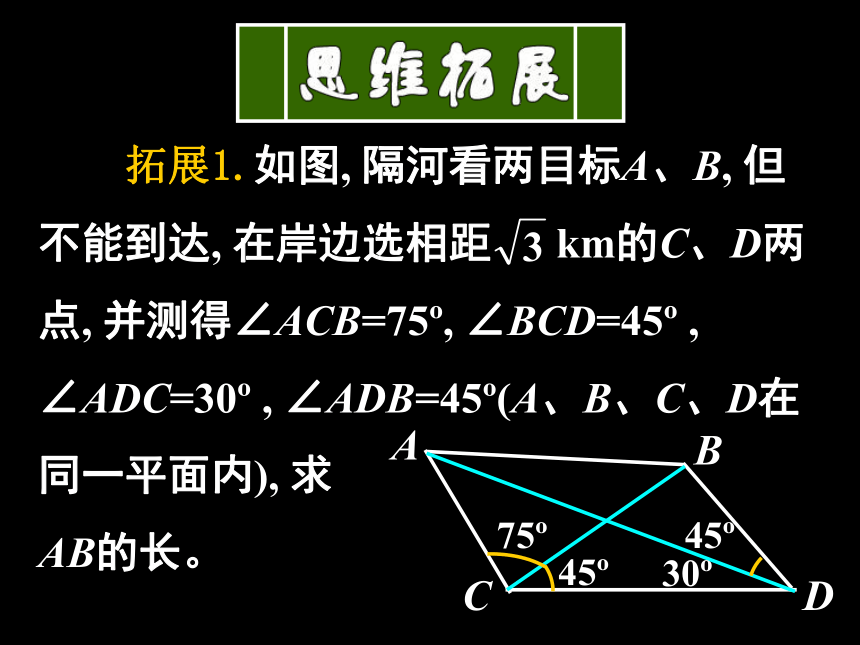
拓展1.如图, 隔河看两目标A、B, 但不能到达, 在岸边选相距 km的C、D两点, 并测得∠ACB=75 , ∠BCD=45 , ∠ADC=30 , ∠ADB=45 (A、B、C、D在同一平面内), 求
AB的长。
C
D
A
B
45
75
45
30
拓展2. 在某海滨城市附近海面有一台风, 据监测, 当前台风中心位于城市O(如图)的东偏南θ方向300km的
海面P处, 并以20km/h的
速度向西偏北45 方向
移动, 台风侵袭的范围
为圆形区域, 当前半径
为60km, 并以10km/h的速度增大, 问几小时后该城市受到台风的侵袭 (其中cosθ= )
北
东
O
Q
P
θ
φ
《学法大视野》第一章第5课时。
应用举例
测量高度
1.正、余弦定理及其推论;
2.实际问题中测量距离的大致思路。
探究1.如图, 在山顶铁塔上B处测得地面上一点A的俯角α=60 , 在塔底C处测得A处的俯角β=45 , 已
知铁塔BC部分的高
为27.3m, 求出山高
CD。(若α=54 40 ,
Β=50 1 呢?)
α
A
B
C
D
β
探究2.如图, 一辆汽车在一条水平的公路上向西行驶, 到A处时测得公路北侧远处一山顶D在西偏北30 的方向上, 行驶5km后到达B处, 测得此山顶在西偏北45 的方向上, 仰角为15 , 求此山的高度CD。
A
B
D
C
探究3.AB是底部B不可到达的一个建筑物, A为建筑物的最高点, 设计一种测量建筑物高度AB的方法。
A
B
探究.测量高度问题一般如何转化成数学问题?
教材P15 练习 T1、T2 、 T3
《学法 大视野》第一章第6课时。
应用举例
测量角度
探究1.如图, 海中有一小岛O, 周围3.8nmile内有暗礁, 一船由西向东航行见此岛在北偏东75 , 船行8nmile后, 望见此岛在北偏东60 , 如果该船不改变航向继续前进, 有没有触礁的危险?
75
A
B
O
60
北
东
探究2.如图, 一艘轮船从A出发, 沿北偏东75 的方向航行70nmile.后到达海岛B, 然后从B出发, 沿北偏东45 的方向航行60nmile到达海岛C, 如果下次航行直接从A出发到C, 此船应
沿怎样的方向航行,
需要航行多少距离?
75
A
B
C
45
北
东
探究3. 如图, 在海岸A处, 发现北偏东45 方向, 距A为 nmile的B处有一艘走私船, 在A处北偏西75 方向, 距A处2nmile的C处辑私船奉命以 nmile/h的速度追截走私船, 此时走私船正以10nmile/h的速度从B处向北偏东30 方向逃窜, 问缉私船沿什么方向能最快追上走私船, 并求出所需时间。
A
B
北
东
C
75
45
30
探究4.测量角度问题如何转化成数学问题?
《学法大视野》第一章第7课时。
应用举例
应用举例
测量距离
解三角形模块
探究1.如图, 设A、B两点在河的两岸, 要测量两点之间的距离, 测量者在A的同侧, 在所在的河岸边选定一点C, 测出AC的距离是42m, ∠BAC=45 , ∠ACB=75 , 求 AB的长.
C
A
B
探究2.如图, A、B两点都在河的对岸, (不可到达), 设计一种测量A、B两点间距离的方法。
A
B
教材P13练习 T1、T2
拓展1.如图, 隔河看两目标A、B, 但不能到达, 在岸边选相距 km的C、D两点, 并测得∠ACB=75 , ∠BCD=45 , ∠ADC=30 , ∠ADB=45 (A、B、C、D在同一平面内), 求
AB的长。
C
D
A
B
45
75
45
30
拓展2. 在某海滨城市附近海面有一台风, 据监测, 当前台风中心位于城市O(如图)的东偏南θ方向300km的
海面P处, 并以20km/h的
速度向西偏北45 方向
移动, 台风侵袭的范围
为圆形区域, 当前半径
为60km, 并以10km/h的速度增大, 问几小时后该城市受到台风的侵袭 (其中cosθ= )
北
东
O
Q
P
θ
φ
《学法大视野》第一章第5课时。
应用举例
测量高度
1.正、余弦定理及其推论;
2.实际问题中测量距离的大致思路。
探究1.如图, 在山顶铁塔上B处测得地面上一点A的俯角α=60 , 在塔底C处测得A处的俯角β=45 , 已
知铁塔BC部分的高
为27.3m, 求出山高
CD。(若α=54 40 ,
Β=50 1 呢?)
α
A
B
C
D
β
探究2.如图, 一辆汽车在一条水平的公路上向西行驶, 到A处时测得公路北侧远处一山顶D在西偏北30 的方向上, 行驶5km后到达B处, 测得此山顶在西偏北45 的方向上, 仰角为15 , 求此山的高度CD。
A
B
D
C
探究3.AB是底部B不可到达的一个建筑物, A为建筑物的最高点, 设计一种测量建筑物高度AB的方法。
A
B
探究.测量高度问题一般如何转化成数学问题?
教材P15 练习 T1、T2 、 T3
《学法 大视野》第一章第6课时。
应用举例
测量角度
探究1.如图, 海中有一小岛O, 周围3.8nmile内有暗礁, 一船由西向东航行见此岛在北偏东75 , 船行8nmile后, 望见此岛在北偏东60 , 如果该船不改变航向继续前进, 有没有触礁的危险?
75
A
B
O
60
北
东
探究2.如图, 一艘轮船从A出发, 沿北偏东75 的方向航行70nmile.后到达海岛B, 然后从B出发, 沿北偏东45 的方向航行60nmile到达海岛C, 如果下次航行直接从A出发到C, 此船应
沿怎样的方向航行,
需要航行多少距离?
75
A
B
C
45
北
东
探究3. 如图, 在海岸A处, 发现北偏东45 方向, 距A为 nmile的B处有一艘走私船, 在A处北偏西75 方向, 距A处2nmile的C处辑私船奉命以 nmile/h的速度追截走私船, 此时走私船正以10nmile/h的速度从B处向北偏东30 方向逃窜, 问缉私船沿什么方向能最快追上走私船, 并求出所需时间。
A
B
北
东
C
75
45
30
探究4.测量角度问题如何转化成数学问题?
《学法大视野》第一章第7课时。
