余弦定理
图片预览









文档简介
(共35张PPT)
余 弦 定 理
一、复习:
一、复习:
正弦定理
一、复习:
正弦定理
应 用 :
应 用 :
1. 两角和任意一边, 求其它两边和一角;
应 用 :
2. 两角和其中一边对角, 求另一边的对 角,进而可求其它的边和角.
1. 两角和任意一边, 求其它两边和一角;
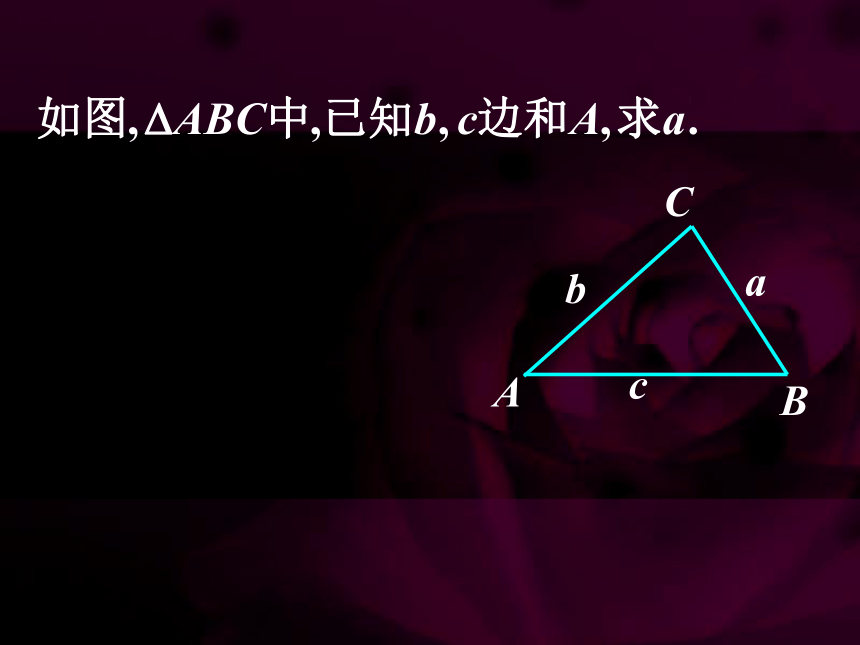
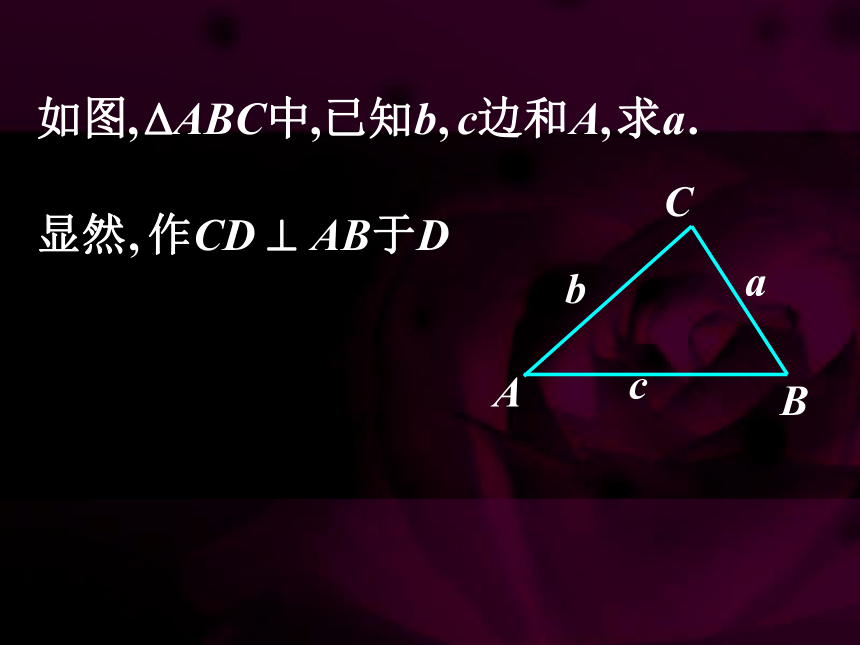
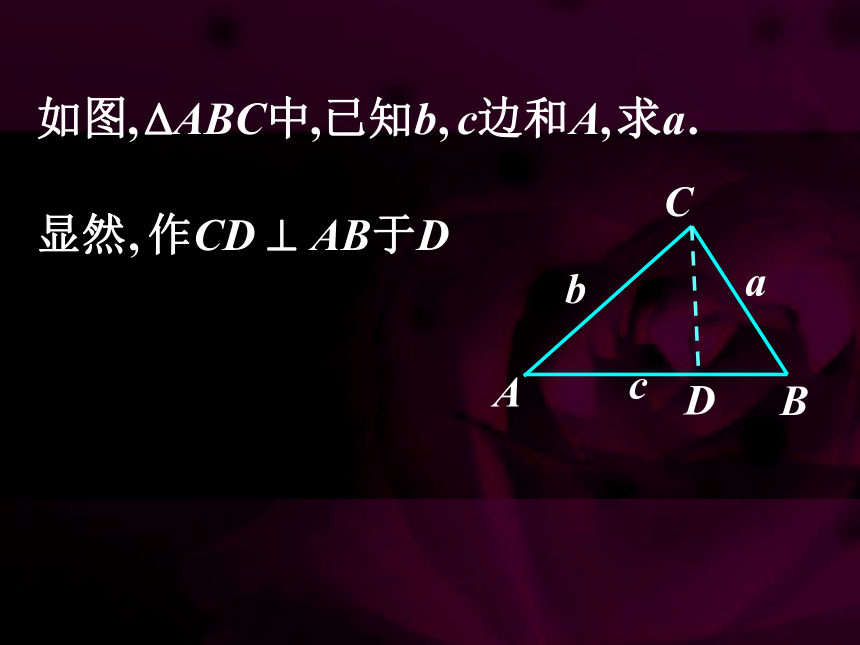
二、猜想命题,证明定理:
二、猜想命题,证明定理:
c
C
A
b
a
B
c
C
A
b
a
B
c
C
A
b
a
B
D
c
C
A
b
a
B
D
c
C
A
b
a
B
D
解法二:向量解法
c
C
A
b
a
B
解法二:向量解法
c
C
A
b
a
B
c
C
A
b
a
B
c
C
A
b
a
B
余 弦 定 理
余 弦 定 理
三角形任何一边的平方等于其它 两边平方的和减去这两边与它们夹角 的余弦的积的两倍.
强 调
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
2. 知三求一.
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
2. 知三求一.
3. 当夹角为90°时, 即三角形为直角三 角形时即为勾股定理(特例).
余弦定理能解决的问题:
余弦定理能解决的问题:
1. 已知三边求角;
余弦定理能解决的问题:
1. 已知三边求角;
2. 已知两边和它们的夹角求第三边.
三、理解定理,初步应用
练习:
课堂练习
拓展练习
余 弦 定 理
一、复习:
一、复习:
正弦定理
一、复习:
正弦定理
应 用 :
应 用 :
1. 两角和任意一边, 求其它两边和一角;
应 用 :
2. 两角和其中一边对角, 求另一边的对 角,进而可求其它的边和角.
1. 两角和任意一边, 求其它两边和一角;
二、猜想命题,证明定理:
二、猜想命题,证明定理:
c
C
A
b
a
B
c
C
A
b
a
B
c
C
A
b
a
B
D
c
C
A
b
a
B
D
c
C
A
b
a
B
D
解法二:向量解法
c
C
A
b
a
B
解法二:向量解法
c
C
A
b
a
B
c
C
A
b
a
B
c
C
A
b
a
B
余 弦 定 理
余 弦 定 理
三角形任何一边的平方等于其它 两边平方的和减去这两边与它们夹角 的余弦的积的两倍.
强 调
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
2. 知三求一.
强 调
1. 熟悉定理的结构, 注意“平方”“夹角” “余弦”等.
2. 知三求一.
3. 当夹角为90°时, 即三角形为直角三 角形时即为勾股定理(特例).
余弦定理能解决的问题:
余弦定理能解决的问题:
1. 已知三边求角;
余弦定理能解决的问题:
1. 已知三边求角;
2. 已知两边和它们的夹角求第三边.
三、理解定理,初步应用
练习:
课堂练习
拓展练习
