正弦定理1
图片预览






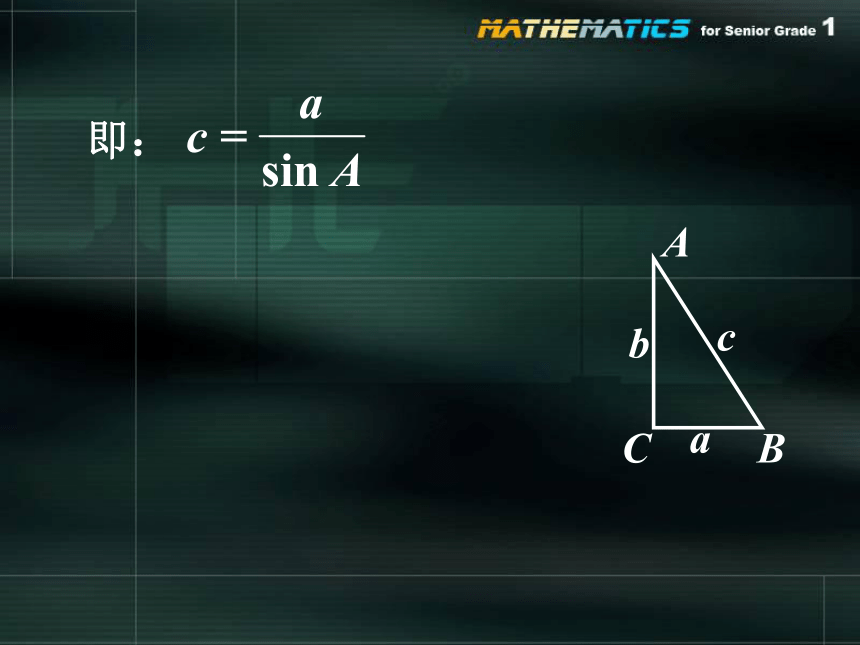
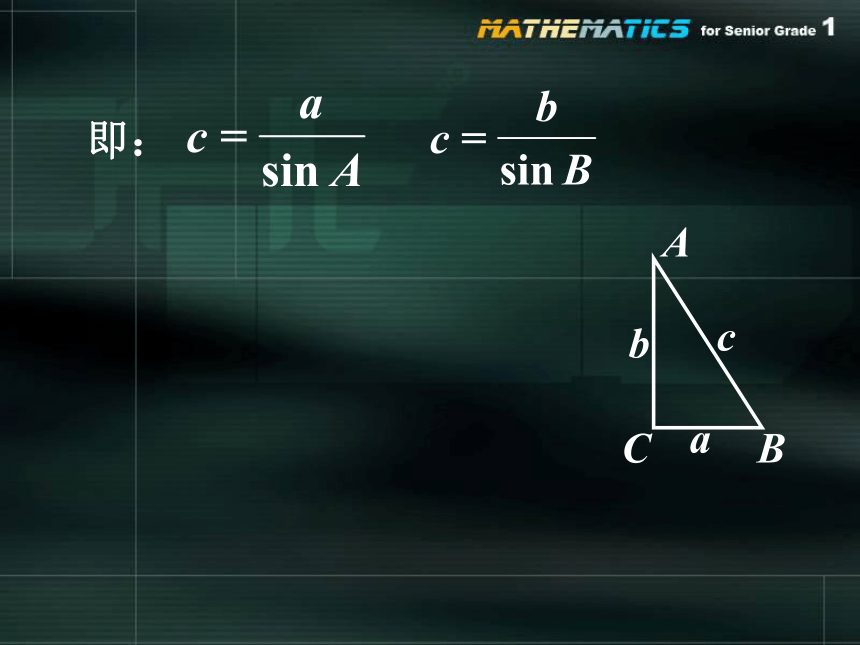
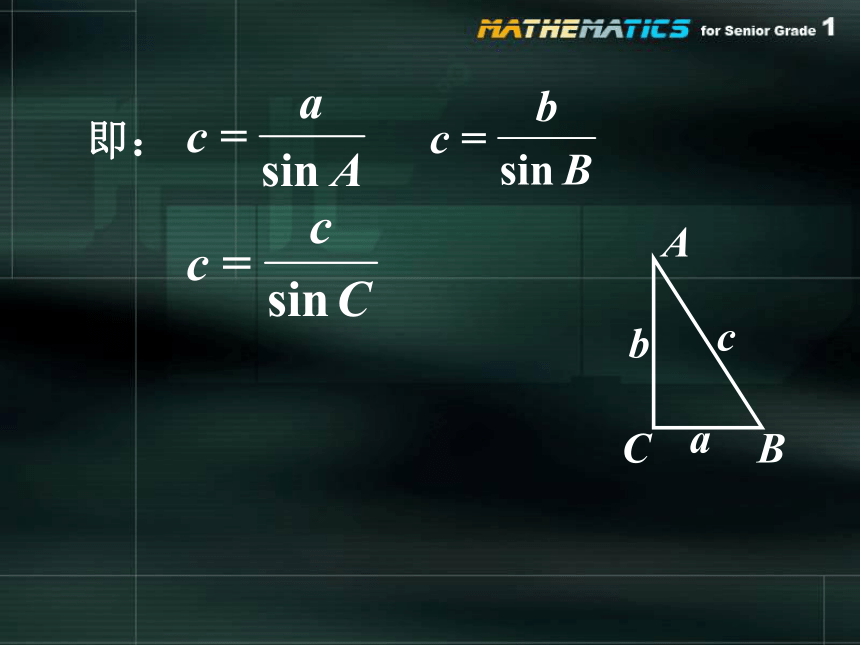
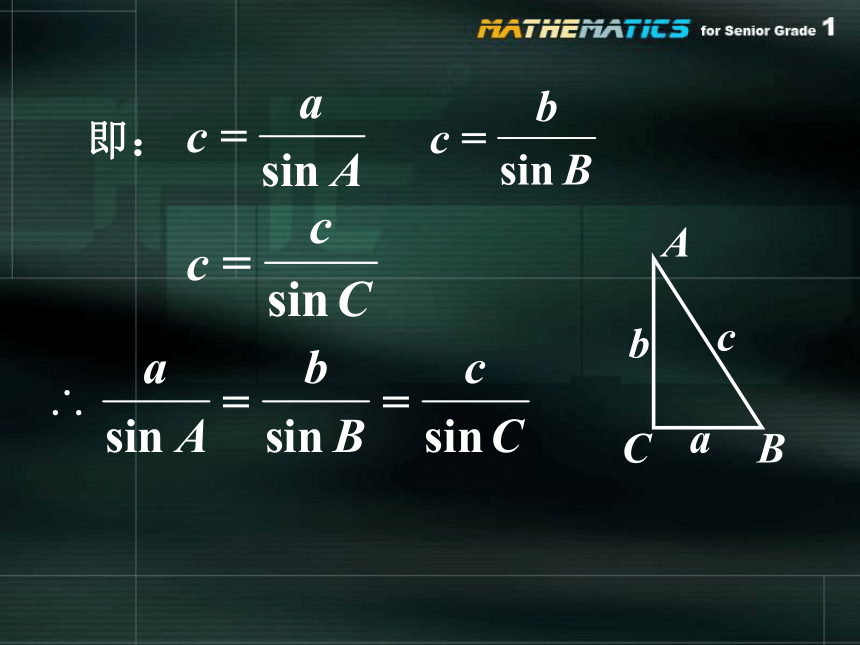

文档简介
(共40张PPT)
正 弦 定 理
一、引 言 :
一、引 言 :
在直角三角形中, 由三角形内角和定理、勾股定理、锐角三角函数, 可以由已知的边和角求出未知的边和角. 那么斜三角形怎么办?
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
以上关系式能否推广到斜三角形?
三、寻找方法,证明定理:
证法一: (传统证法)
三、寻找方法,证明定理:
证法一: (传统证法)
A
C
B
a
b
c
证法二: (能否将角转化到直角三角形中 )
证法二: (能否将角转化到直角三角形中 )
A
C
B
b
a
c
C '
A
C
B
b
a
c
C '
证法三: (能否用向量知识来证明 )
证法三: (能否用向量知识来证明 )
这里涉及到三角形中的边角关系,而向量中的数量积则反应了边角关系.
证法三: (能否用向量知识来证明 )
这里涉及到三角形中的边角关系,而向量中的数量积则反应了边角关系.
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
正 弦 定 理
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意
四、理解定理,初步应用:
利用正弦定理可以解决哪些三角形问题
思 考
利用正弦定理可以解决哪些三角形问题
1. 两角和任意一边,求其它两边和一角;
思 考
利用正弦定理可以解决哪些三角形问题
1. 两角和任意一边,求其它两边和一角;
2. 两边和其中一边对角,求另一边的对 角,进而可求其它的边和角.
思 考
练 习
练 习
正 弦 定 理
一、引 言 :
一、引 言 :
在直角三角形中, 由三角形内角和定理、勾股定理、锐角三角函数, 可以由已知的边和角求出未知的边和角. 那么斜三角形怎么办?
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
二、提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
即:
A
C
B
b
a
c
以上关系式能否推广到斜三角形?
三、寻找方法,证明定理:
证法一: (传统证法)
三、寻找方法,证明定理:
证法一: (传统证法)
A
C
B
a
b
c
证法二: (能否将角转化到直角三角形中 )
证法二: (能否将角转化到直角三角形中 )
A
C
B
b
a
c
C '
A
C
B
b
a
c
C '
证法三: (能否用向量知识来证明 )
证法三: (能否用向量知识来证明 )
这里涉及到三角形中的边角关系,而向量中的数量积则反应了边角关系.
证法三: (能否用向量知识来证明 )
这里涉及到三角形中的边角关系,而向量中的数量积则反应了边角关系.
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
正 弦 定 理
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意
四、理解定理,初步应用:
利用正弦定理可以解决哪些三角形问题
思 考
利用正弦定理可以解决哪些三角形问题
1. 两角和任意一边,求其它两边和一角;
思 考
利用正弦定理可以解决哪些三角形问题
1. 两角和任意一边,求其它两边和一角;
2. 两边和其中一边对角,求另一边的对 角,进而可求其它的边和角.
思 考
练 习
练 习
