沪科版数学七年级下册:8.2 整式乘法 2课时 课件(共30张PPT)
文档属性
| 名称 | 沪科版数学七年级下册:8.2 整式乘法 2课时 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 667.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-27 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
单项式与单项式相乘
整式乘法
知识回顾
前面我们学习了哪些幂的运算?
运算方法分别是什么?
第一课时
运用幂的运算性质计算下列各题:
光的速度大约是3×105km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球。1年以3×107s计算,试问地球与这颗恒星的距离约为多少千米?
分析:距离=速度×时间;即(3×105)×(4×3×107);
怎样计算(3×105)×(
4×3×107
)?
合作探究
地球与太阳的距离约是:
(3×105)×(4×3×107)
=4×3
×3
×
105
×107
=4×32×105
×107
=3.6
×1013(km)
因此,地球与这颗恒星的距离约为3.6
×1013
km
(1)上面的运算应用了哪些性质呢?
(3×105)×(4×3×107)
=4×3
×3
×
105
×107
=4×32×105
×107
=3.6
×1013(km)
乘法分配律
乘法结合律
(2)如何计算bc5·abc7?
bc5?abc7是两个单项式bc5与abc7相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:
bc5?abc7
=a?
(b?b)?(c5?c7)
=ab2c5+7=ab2c12
归纳总结
单项式与单项式相乘的法则:
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
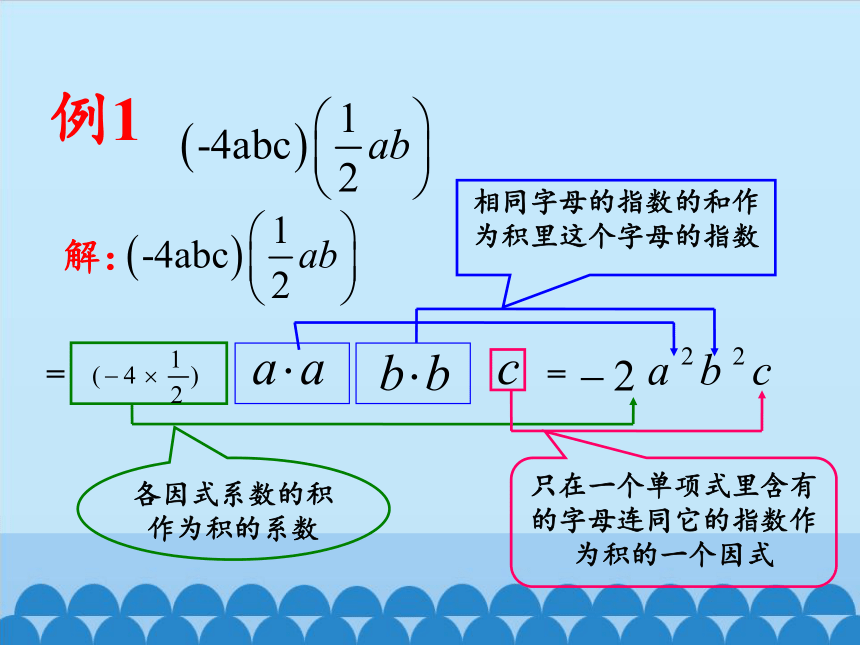
例1
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
完成下列计算:
4x2y·3xy2=(4×3)
·(x2·__)(y·__)=____
5abc·(-3ab)=
〔
5×(-3)
〕·(a·_)(b·_)
·c=_______
x
y2
12x3y3
a
b
-15a2b2c
只在一个单项式里含有的字母要连同它的指数写在积里(注意不要把这个因式丢掉)
注:单项式相乘的结果仍是单项式
口答
(
)
(
)
(
)
(
)
×
×
×
×
6
c
5
—
练习
一
计算:
(-5a2b)(-3a);
(2)
(2x)3(-5xy2)。
练习
二
计算:
(1)2x2·3x3
(2)
a2b3·
abc
?
?
(3)(-2.5x2)
·(-4x)
2
(4)
(-4x2y)
·(-xy)
2
(-
y3)
小结
回顾交流:
本节课我们学习了那些内容?
单项式乘以单项式的依据是什么?
如何进行单项式与单项式乘法运算?
复习回顾
1.单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式相乘的结果仍是单项式。
2.计算步骤
有乘方先算乘方,然后再相乘;
(2)把系数的积作为积的系数;
(3)同底数幂相乘的积作为积的因式;
(4)只在一个单项式里含有的字母,要连同它的指数写在积里。
第二课时
合作探究
思考:
怎样计算
?
大家开动脑筋,看看有什么方法?
计算
,就是要求一个单项式,使它与
相乘的积等于
。
因为
所以
分析
得到什么规律?
单项式除法法则
单项式相除,把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
对比学习
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
单项式相乘
单项式相除
第一步
第二步
第三步
试一试
例2
计算:
解:
练一练
注意运算顺序:先乘方,再乘除,最后算加减
例3
“卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道。
(1)它的这一行程相当于地球赤道多少圈?(已知地球半径约6.4×103km,π取3.14
)
(2)这一行程如果由速度是100km/h的汽车来完成,需要行驶多少年?(1年按365天计算)
(3)这一行程如果由速度是10m/s的短跑飞人来完成,需要跑多少年?
解:
所以探测器的行程相当于地球赤道约87000圈
所以探测器的行程相当于由速度是100km/h的汽车行驶约4000年
所以探测器的行程相当于由速度是10m/s的短跑飞人跑约11000年
你还能用什么方法,让人感受到
3.5×109km的长度?
课本随堂练习
练一练
1.单项式与单项式相除的法则
单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的因式。
2.对比的学习方法
谈谈你的收获
1.基础作业:习题
作业
2.拓展作业:在一次水灾中,大约有2.5×105个人无家可归。假若一顶帐篷占地100
m2
,可以安置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约占多大地方?估计你学校的操场中可以安置多少人?要安置这些人,大约要多少个这样的操场?
精心选一选:
1.下列计算中,正确的是(
)
A.2a3·3a2=6a6
B.4x3·2x5=8x8
C.2X·2X5=4X5
D.5X3·4X4=9X7
2.下列运算正确的是(
)
A.X2·X3=X6
B.X2+X2=2X4
C.(-2X)2=-4X2
D.(-2X2)(-3X3)=6x5
B
D
选作:
谢
谢
单项式与单项式相乘
整式乘法
知识回顾
前面我们学习了哪些幂的运算?
运算方法分别是什么?
第一课时
运用幂的运算性质计算下列各题:
光的速度大约是3×105km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球。1年以3×107s计算,试问地球与这颗恒星的距离约为多少千米?
分析:距离=速度×时间;即(3×105)×(4×3×107);
怎样计算(3×105)×(
4×3×107
)?
合作探究
地球与太阳的距离约是:
(3×105)×(4×3×107)
=4×3
×3
×
105
×107
=4×32×105
×107
=3.6
×1013(km)
因此,地球与这颗恒星的距离约为3.6
×1013
km
(1)上面的运算应用了哪些性质呢?
(3×105)×(4×3×107)
=4×3
×3
×
105
×107
=4×32×105
×107
=3.6
×1013(km)
乘法分配律
乘法结合律
(2)如何计算bc5·abc7?
bc5?abc7是两个单项式bc5与abc7相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:
bc5?abc7
=a?
(b?b)?(c5?c7)
=ab2c5+7=ab2c12
归纳总结
单项式与单项式相乘的法则:
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
例1
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
完成下列计算:
4x2y·3xy2=(4×3)
·(x2·__)(y·__)=____
5abc·(-3ab)=
〔
5×(-3)
〕·(a·_)(b·_)
·c=_______
x
y2
12x3y3
a
b
-15a2b2c
只在一个单项式里含有的字母要连同它的指数写在积里(注意不要把这个因式丢掉)
注:单项式相乘的结果仍是单项式
口答
(
)
(
)
(
)
(
)
×
×
×
×
6
c
5
—
练习
一
计算:
(-5a2b)(-3a);
(2)
(2x)3(-5xy2)。
练习
二
计算:
(1)2x2·3x3
(2)
a2b3·
abc
?
?
(3)(-2.5x2)
·(-4x)
2
(4)
(-4x2y)
·(-xy)
2
(-
y3)
小结
回顾交流:
本节课我们学习了那些内容?
单项式乘以单项式的依据是什么?
如何进行单项式与单项式乘法运算?
复习回顾
1.单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式相乘的结果仍是单项式。
2.计算步骤
有乘方先算乘方,然后再相乘;
(2)把系数的积作为积的系数;
(3)同底数幂相乘的积作为积的因式;
(4)只在一个单项式里含有的字母,要连同它的指数写在积里。
第二课时
合作探究
思考:
怎样计算
?
大家开动脑筋,看看有什么方法?
计算
,就是要求一个单项式,使它与
相乘的积等于
。
因为
所以
分析
得到什么规律?
单项式除法法则
单项式相除,把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
对比学习
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
单项式相乘
单项式相除
第一步
第二步
第三步
试一试
例2
计算:
解:
练一练
注意运算顺序:先乘方,再乘除,最后算加减
例3
“卡西尼”号土星探测器历经7年多、行程约3.5×109km后进入环绕土星运行的轨道。
(1)它的这一行程相当于地球赤道多少圈?(已知地球半径约6.4×103km,π取3.14
)
(2)这一行程如果由速度是100km/h的汽车来完成,需要行驶多少年?(1年按365天计算)
(3)这一行程如果由速度是10m/s的短跑飞人来完成,需要跑多少年?
解:
所以探测器的行程相当于地球赤道约87000圈
所以探测器的行程相当于由速度是100km/h的汽车行驶约4000年
所以探测器的行程相当于由速度是10m/s的短跑飞人跑约11000年
你还能用什么方法,让人感受到
3.5×109km的长度?
课本随堂练习
练一练
1.单项式与单项式相除的法则
单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的因式。
2.对比的学习方法
谈谈你的收获
1.基础作业:习题
作业
2.拓展作业:在一次水灾中,大约有2.5×105个人无家可归。假若一顶帐篷占地100
m2
,可以安置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约占多大地方?估计你学校的操场中可以安置多少人?要安置这些人,大约要多少个这样的操场?
精心选一选:
1.下列计算中,正确的是(
)
A.2a3·3a2=6a6
B.4x3·2x5=8x8
C.2X·2X5=4X5
D.5X3·4X4=9X7
2.下列运算正确的是(
)
A.X2·X3=X6
B.X2+X2=2X4
C.(-2X)2=-4X2
D.(-2X2)(-3X3)=6x5
B
D
选作:
谢
谢
