人教版九年级下册数学:27.2.2 相似三角形的性质 (共17张PPT)
文档属性
| 名称 | 人教版九年级下册数学:27.2.2 相似三角形的性质 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 695.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 07:46:04 | ||
图片预览


文档简介
(共17张PPT)
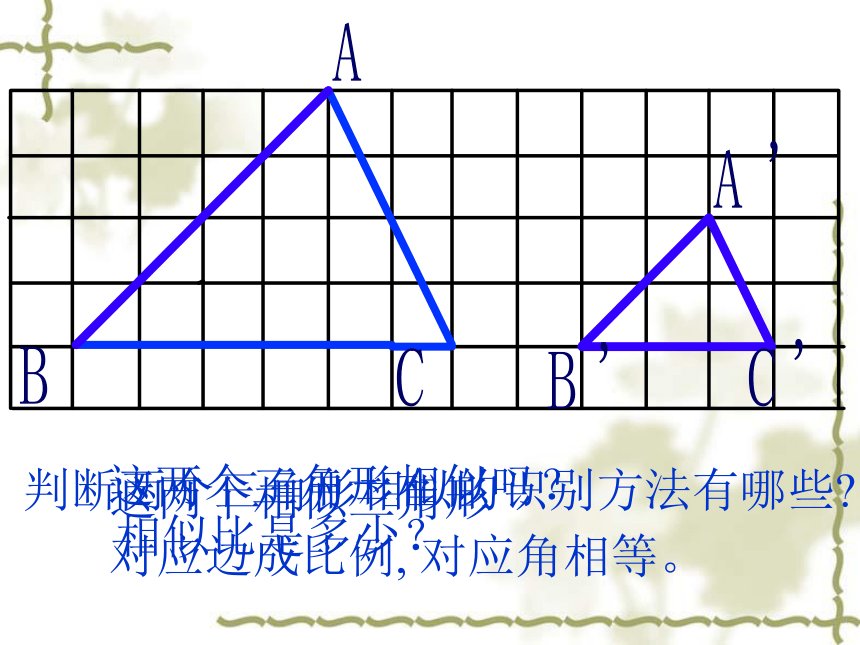
这两个三角形相似吗?
相似比是多少?
这两个相似三角形
对应边成比例,
对应角相等。
判断两个三角形相似的识别方法有哪些?
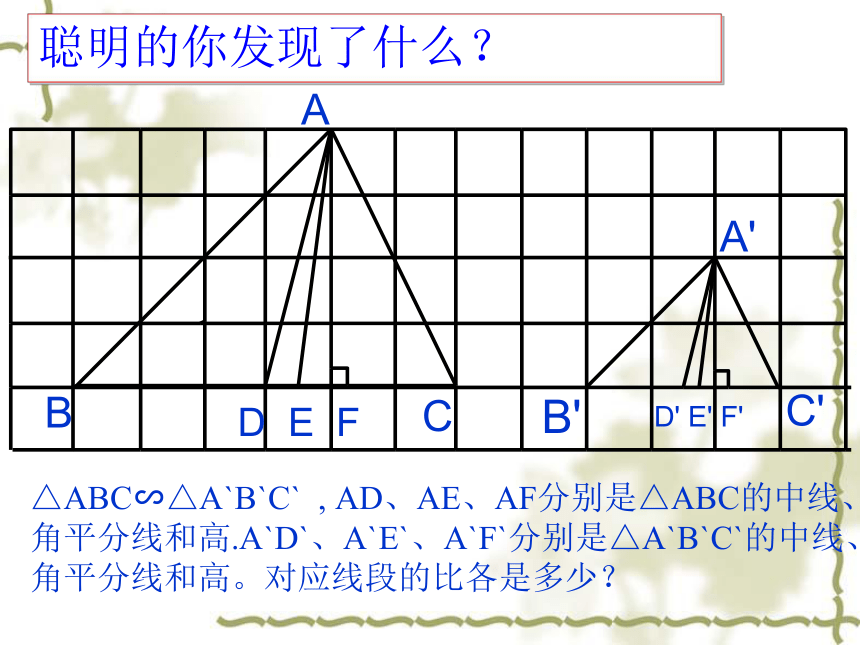
聪明的你发现了什么?
△ABC∽△A`B`C`
,
AD、AE、AF分别是△ABC的中线、角平分线和高.A`D`、A`E`、A`F`分别是△A`B`C`的中线、角平分线和高。对应线段的比各是多少?
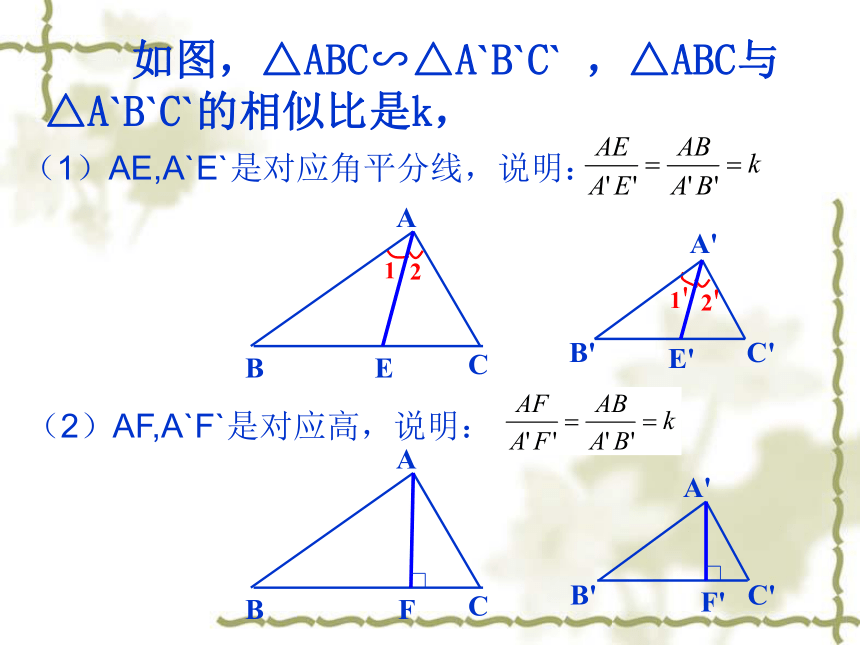
如图,△ABC∽△A`B`C`
,△ABC与△A`B`C`的相似比是k,
(1)AE,A`E`是对应角平分线,说明:
(2)AF,A`F`是对应高,说明:
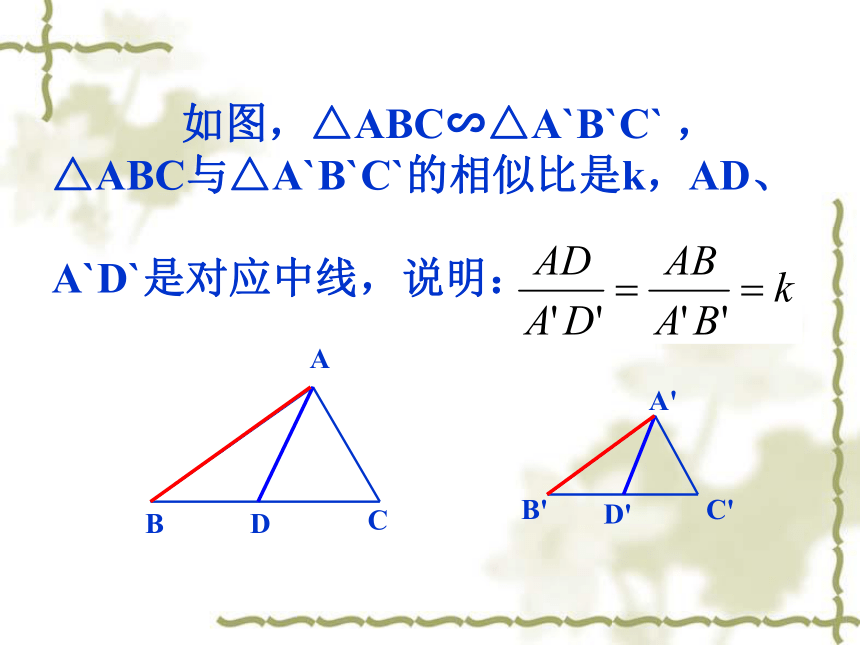
如图,△ABC∽△A`B`C`
,△ABC与△A`B`C`的相似比是k,AD、
A`D`是对应中线,说明:
总结:
相似三角形的对应高、对应角平分线、对应中线的比都等于相似比.
相似三角形对应线段的比等于相似比。
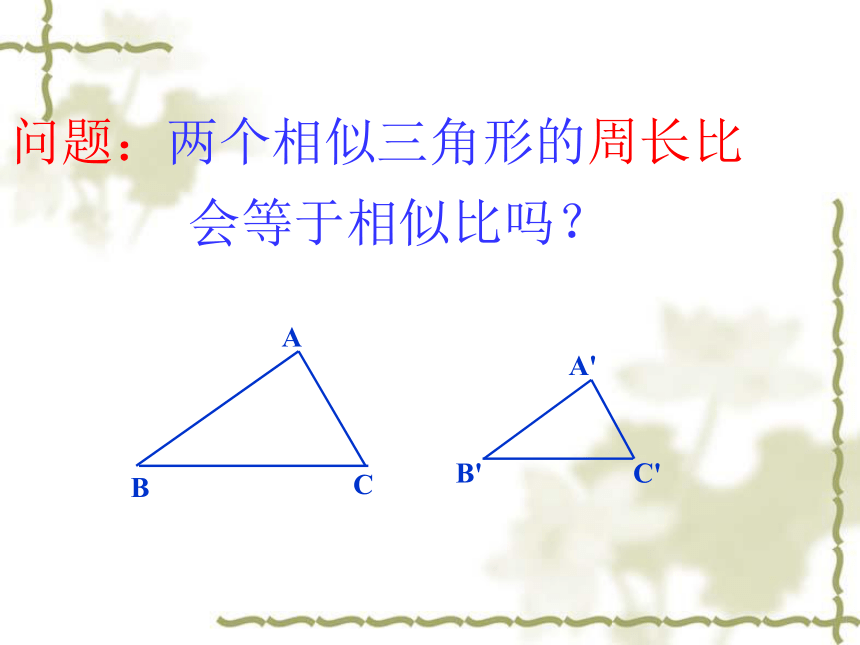
问题:两个相似三角形的周长比
会等于相似比吗?
已知△ABC∽△
,且相似比为k。
求证:△ABC、
周长的比等于k
证明:
△ABC∽△
即△ABC、△
的周长比等于相似比
∵
∴
∴
结论:相似三角形对应角的周长的比等于相似比.
问题:两个相似三角形的面积与
相似三角形的性质
相似比之间有什么关系呢?
例:已知△ABC∽△
,且相似比为k,AD、
分别是△ABC、△
对应边BC、
上的高,求证:
证明:
∵△ABC∽△
∴
∴
结论:相似三角形面积的比等于相似比的平方.
1、如图,AD=3,BD=1,DE∥BC,DF∥AC,EG∥AB。
(1)△ADE和△EGC的相似比是
,对应高的比是
。
(2)
△ABC和△DBF的相似比
,对应角平分线的比
,对应中线的比是
。
3∶
1
4
∶1
4
∶1
4
∶1
3
∶1
2、两个相似三角形各自的最长边分别是7cm、
5cm,它们的对应高的比是_____________
。
7
∶5
达标检测
3、已知△ABC∽△A?B?C?,AD、A
?D
?分别是对应边BC、B
?C
?上的高,若BC=8cm,B
?C
?=6cm,AD=4cm,则A
?D
?等于(
)
A
16cm
B
12
cm
C
3
cm
D
6
cm
4、两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为(
)
A
7∶3
B
49∶9
C
9∶49
D
3∶7
C
D
5、已知△ABC∽△DEF,BG、EH分别是△ABC和
△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵
△ABC∽△DEF
∴ BC∶EF=BG∶EH
即:6∶4=4.8∶EH
∴
EH=3.2(cm)
答:EH的长为3.2cm。
(1)△ADE与△ABC相似吗?如果相似,
求它们的相似比.
A
B
C
D
E
1∶4
(2)
△ADE的周长︰△ABC的周长=_______.
1∶4
例:如图,DE∥BC,
DE
=
1,
BC
=
4,
(4)
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
拓展训练
2、如图,FG//BC,AD⊥BC,
D是垂足,FG=6,BC=15,则
(1)AE:AD是多少?
(2)若AD=10,求ED的长
总结:
(1)你今天的收获是什么?
(2)你对自己或同学的表现满意吗?对自己或同学说一说
同学们
再见
这两个三角形相似吗?
相似比是多少?
这两个相似三角形
对应边成比例,
对应角相等。
判断两个三角形相似的识别方法有哪些?
聪明的你发现了什么?
△ABC∽△A`B`C`
,
AD、AE、AF分别是△ABC的中线、角平分线和高.A`D`、A`E`、A`F`分别是△A`B`C`的中线、角平分线和高。对应线段的比各是多少?
如图,△ABC∽△A`B`C`
,△ABC与△A`B`C`的相似比是k,
(1)AE,A`E`是对应角平分线,说明:
(2)AF,A`F`是对应高,说明:
如图,△ABC∽△A`B`C`
,△ABC与△A`B`C`的相似比是k,AD、
A`D`是对应中线,说明:
总结:
相似三角形的对应高、对应角平分线、对应中线的比都等于相似比.
相似三角形对应线段的比等于相似比。
问题:两个相似三角形的周长比
会等于相似比吗?
已知△ABC∽△
,且相似比为k。
求证:△ABC、
周长的比等于k
证明:
△ABC∽△
即△ABC、△
的周长比等于相似比
∵
∴
∴
结论:相似三角形对应角的周长的比等于相似比.
问题:两个相似三角形的面积与
相似三角形的性质
相似比之间有什么关系呢?
例:已知△ABC∽△
,且相似比为k,AD、
分别是△ABC、△
对应边BC、
上的高,求证:
证明:
∵△ABC∽△
∴
∴
结论:相似三角形面积的比等于相似比的平方.
1、如图,AD=3,BD=1,DE∥BC,DF∥AC,EG∥AB。
(1)△ADE和△EGC的相似比是
,对应高的比是
。
(2)
△ABC和△DBF的相似比
,对应角平分线的比
,对应中线的比是
。
3∶
1
4
∶1
4
∶1
4
∶1
3
∶1
2、两个相似三角形各自的最长边分别是7cm、
5cm,它们的对应高的比是_____________
。
7
∶5
达标检测
3、已知△ABC∽△A?B?C?,AD、A
?D
?分别是对应边BC、B
?C
?上的高,若BC=8cm,B
?C
?=6cm,AD=4cm,则A
?D
?等于(
)
A
16cm
B
12
cm
C
3
cm
D
6
cm
4、两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为(
)
A
7∶3
B
49∶9
C
9∶49
D
3∶7
C
D
5、已知△ABC∽△DEF,BG、EH分别是△ABC和
△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵
△ABC∽△DEF
∴ BC∶EF=BG∶EH
即:6∶4=4.8∶EH
∴
EH=3.2(cm)
答:EH的长为3.2cm。
(1)△ADE与△ABC相似吗?如果相似,
求它们的相似比.
A
B
C
D
E
1∶4
(2)
△ADE的周长︰△ABC的周长=_______.
1∶4
例:如图,DE∥BC,
DE
=
1,
BC
=
4,
(4)
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
拓展训练
2、如图,FG//BC,AD⊥BC,
D是垂足,FG=6,BC=15,则
(1)AE:AD是多少?
(2)若AD=10,求ED的长
总结:
(1)你今天的收获是什么?
(2)你对自己或同学的表现满意吗?对自己或同学说一说
同学们
再见
