人教版九年级下册数学:第二十八章 锐角三角函数 专题复习课件 (共23张PPT)
文档属性
| 名称 | 人教版九年级下册数学:第二十八章 锐角三角函数 专题复习课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 577.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-27 17:57:09 | ||
图片预览





文档简介
(共23张PPT)
锐角三角函数专题复习
点击添加文本
点击添加文本
点击添加文本
点击添加文本
主要内容
1.旧知梳理,聚焦中考
2.考点探究,对点演练
3.课堂小结,总结提升
1.旧知梳理,聚焦中考
考点一
锐角三角函数定义
考点二
特殊锐角的三角函数值
考点三
解直角三角形
1.旧知梳理,聚焦中考
正弦
正切
余弦
考点一
锐角三角函数定义
1.旧知梳理,聚焦中考
sinα
tanα
cosα
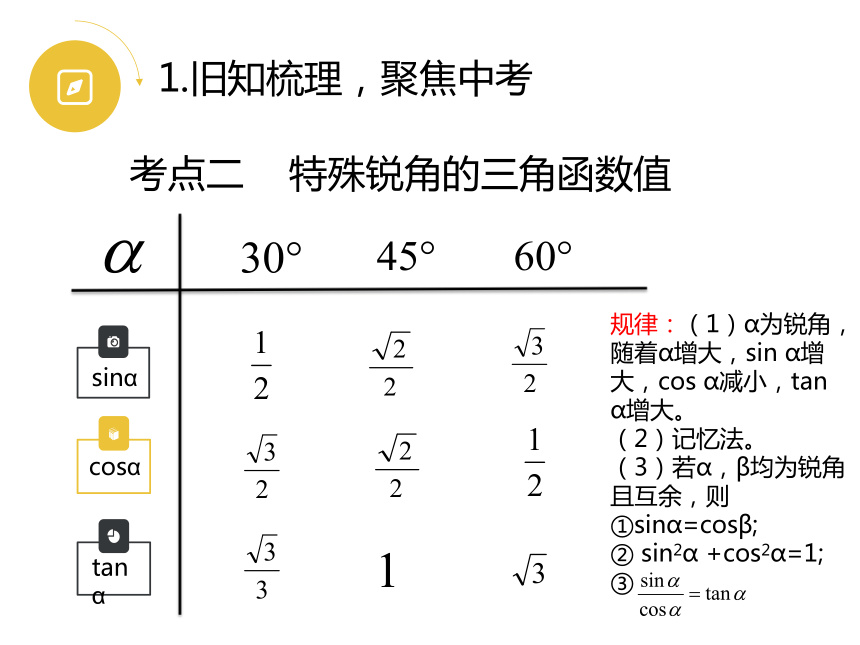
考点二
特殊锐角的三角函数值
规律:(1)α为锐角,随着α增大,sin
α增大,cos
α减小,tan
α增大。
(2)记忆法。
(3)若α,β均为锐角且互余,则
①sinα=cosβ;
②
sin2α
+cos2α=1;
③
1.旧知梳理,聚焦中考
考点三
解直角三角形
1.定义:一般地,直角三角形中,除直角外共有五个元素,即三条边和两个锐角。由直角三角形中的已知元素求出其余未知元素的过程叫做解直角三角形。
2.解直角三角形的常用关系
3.常见题型
(1)已知一边一角
①已知斜边和一个锐角;②已知一直角边和一个锐角。
(2)已知两边
①已知斜边和一直角边;②已知两条直角边。
2.考点探究,对点演连
探究一
求锐角三角函数值
探究二
特殊锐角的三角函数值的应用
探究三
解直角三角形
探究四
解直角三角形的简单应用
2.考点探究,对点演连
探究一
求锐角三角函数值
命题角度:
(1)已知直角三角形的边长,直接求锐角三角函数值;
(2)在网格中求锐角三角函数值。
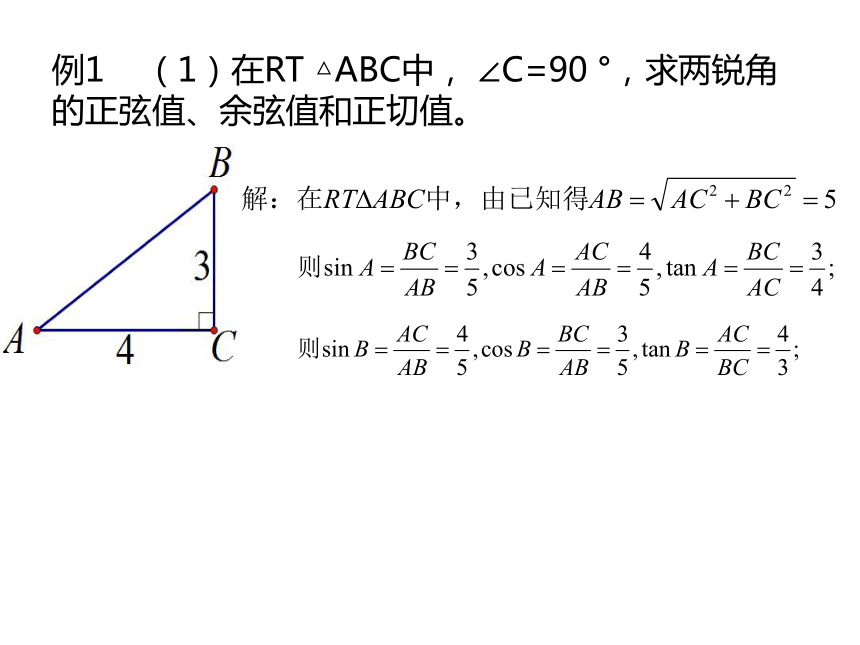
例1
(1)在RT
△ABC中,
∠C=90
°,求两锐角的正弦值、余弦值和正切值。
例1
(2)已知在正方形方格图形中,小正方形的顶点称为格点,△ABC的三个顶点均在格点上,则sinA的值为_______
针对训练
(1)RT△ABC中,
求两锐角的正弦值、余弦值和正切值。
(2)△ABC的三个顶点均在格点上,则∠BAC的正弦值为_______
2.考点探究,对点演连
探究二
特殊锐角的三角函数值的应用
命题角度:
(1)直接写30°,45°,60°角的三角函数值;
(2)已知特殊三角函数值,求角度。
例2
(1)计算:
(2)
解:
(2)由题意可知
B为锐角,因此
针对训练
(1)计算①
②
2.考点探究,对点演连
探究三
解直角三角形
命题角度:
(1)利用锐角三角函数解直角三角形;
(2)将斜三角形或不规则图形化归为直角三角形
解决问题。
例3
针对训练
D
2.考点探究,对点演连
探究四
解直角三角形的简单应用
命题角度:
利用直角三角形解决与高度、宽度、坡度、方
向角有关的问题;(仰角、俯角、方向角、坡度等
定义,坡度指坡面的铅直高度与水平宽度之比)
例4
热气球探测显示,从热气球看一栋楼顶部的仰角为30°,看楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果保留根号)?
D
针对训练
如图,海中有一个小岛A,它周围8n
mile
内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12
n
mile到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
3.课堂小结
,总结提升
1.锐角三角函数定义
2.特殊角的锐角三角函数值及其应用
3.解直角三角形
4.解直角三角形的简单应用
某地一天桥如图所示,天桥高6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1:
。
①求新坡面的坡脚
。
②原天桥底部正前方8米(PB的长)处的文化墙PM是否需要拆除?请说明理由。
课后练习
点击添加文本
点击添加文本
点击添加文本
点击添加文本
谢谢!
锐角三角函数专题复习
点击添加文本
点击添加文本
点击添加文本
点击添加文本
主要内容
1.旧知梳理,聚焦中考
2.考点探究,对点演练
3.课堂小结,总结提升
1.旧知梳理,聚焦中考
考点一
锐角三角函数定义
考点二
特殊锐角的三角函数值
考点三
解直角三角形
1.旧知梳理,聚焦中考
正弦
正切
余弦
考点一
锐角三角函数定义
1.旧知梳理,聚焦中考
sinα
tanα
cosα
考点二
特殊锐角的三角函数值
规律:(1)α为锐角,随着α增大,sin
α增大,cos
α减小,tan
α增大。
(2)记忆法。
(3)若α,β均为锐角且互余,则
①sinα=cosβ;
②
sin2α
+cos2α=1;
③
1.旧知梳理,聚焦中考
考点三
解直角三角形
1.定义:一般地,直角三角形中,除直角外共有五个元素,即三条边和两个锐角。由直角三角形中的已知元素求出其余未知元素的过程叫做解直角三角形。
2.解直角三角形的常用关系
3.常见题型
(1)已知一边一角
①已知斜边和一个锐角;②已知一直角边和一个锐角。
(2)已知两边
①已知斜边和一直角边;②已知两条直角边。
2.考点探究,对点演连
探究一
求锐角三角函数值
探究二
特殊锐角的三角函数值的应用
探究三
解直角三角形
探究四
解直角三角形的简单应用
2.考点探究,对点演连
探究一
求锐角三角函数值
命题角度:
(1)已知直角三角形的边长,直接求锐角三角函数值;
(2)在网格中求锐角三角函数值。
例1
(1)在RT
△ABC中,
∠C=90
°,求两锐角的正弦值、余弦值和正切值。
例1
(2)已知在正方形方格图形中,小正方形的顶点称为格点,△ABC的三个顶点均在格点上,则sinA的值为_______
针对训练
(1)RT△ABC中,
求两锐角的正弦值、余弦值和正切值。
(2)△ABC的三个顶点均在格点上,则∠BAC的正弦值为_______
2.考点探究,对点演连
探究二
特殊锐角的三角函数值的应用
命题角度:
(1)直接写30°,45°,60°角的三角函数值;
(2)已知特殊三角函数值,求角度。
例2
(1)计算:
(2)
解:
(2)由题意可知
B为锐角,因此
针对训练
(1)计算①
②
2.考点探究,对点演连
探究三
解直角三角形
命题角度:
(1)利用锐角三角函数解直角三角形;
(2)将斜三角形或不规则图形化归为直角三角形
解决问题。
例3
针对训练
D
2.考点探究,对点演连
探究四
解直角三角形的简单应用
命题角度:
利用直角三角形解决与高度、宽度、坡度、方
向角有关的问题;(仰角、俯角、方向角、坡度等
定义,坡度指坡面的铅直高度与水平宽度之比)
例4
热气球探测显示,从热气球看一栋楼顶部的仰角为30°,看楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果保留根号)?
D
针对训练
如图,海中有一个小岛A,它周围8n
mile
内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12
n
mile到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
3.课堂小结
,总结提升
1.锐角三角函数定义
2.特殊角的锐角三角函数值及其应用
3.解直角三角形
4.解直角三角形的简单应用
某地一天桥如图所示,天桥高6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1:
。
①求新坡面的坡脚
。
②原天桥底部正前方8米(PB的长)处的文化墙PM是否需要拆除?请说明理由。
课后练习
点击添加文本
点击添加文本
点击添加文本
点击添加文本
谢谢!
