初中数学中考几何模型学案
图片预览


文档简介
中考数学几何模型
1、角平分线模型
基本思路:利用角平分线的性质。
(1)三角形内角、外角平分线
OB、OC分别平分∠ABC和∠ACB,则∠O=90°+∠A。
BD、CD为△ABC的外角平分线,则∠D=90°-∠A。
BD平分∠ABC,CD为△ABC的外角平分线,则∠D=∠A。
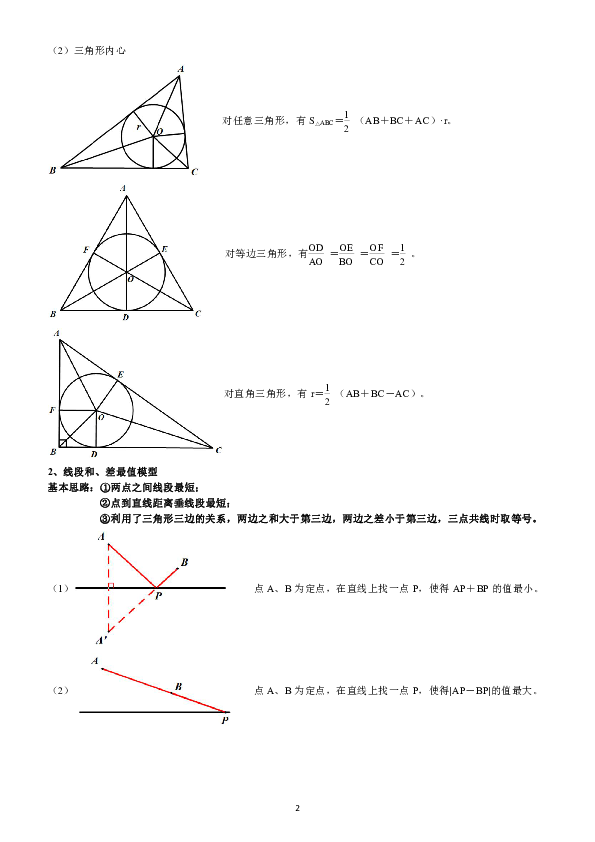
(2)三角形内心
对任意三角形,有S△ABC=(AB+BC+AC)·r。
对等边三角形,有===。
对直角三角形,有r=(AB+BC-AC)。
2、线段和、差最值模型
基本思路:①两点之间线段最短;
②点到直线距离垂线段最短;
③利用了三角形三边的关系,两边之和大于第三边,两边之差小于第三边,三点共线时取等号。
(1)
点A、B为定点,在直线上找一点P,使得AP+BP的值最小。
(2)
点A、B为定点,在直线上找一点P,使得|AP-BP|的值最大。
(3)
点A、B为定点,在直线上找一点P,使得AP+BP的值最小。
(4)点A、B为定点,在直线上找一点P,使得|AP-BP|的值最大。
(5)
(6)
(7)
(8)
(9)
(10)费马点:①若△ABC内角都小于120°,则能在△ABC内找一点P,使PA+PB+PC的值最小。
②若△ABC有一个内角不小于120°,则△ABC内使PA+PB+PC的值最小的点
P就在钝角所在顶点。
(11)
圆所有的弦中,直径最长。
(12)点P为圆外一定点,点Q为圆上一动点,则PB≤PQ≤PA。
3、旋转模型
基本思路:利用旋转图形的性质。
(1)等腰三角形旋转(两个顶角相等的等腰三角形顶角重合,其中一个三角形绕顶点旋转。)
无论什么三角形,均有△ABD≌△ACE。
(2)正方形旋转
4、半角模型
基本思路:旋转后找全等或相似,利用好含特殊角(30°、45°、60°)的直角三角形边之间的关系。
(1)等腰直角三角形半角模型
MN2=BM2+CN2
(2)顶角为120°等腰三角形半角模型
BM2+NC2-MN2=BM×NC(余弦定理)
一般来说,BM、MN、NC没有特定的关系,当BM:MN:NC=2::1时,∠BDM=90°。
(3)等边三角形与顶角为120°等腰三角形半角模型
BE+CF=EF
(4)正方形半角模型
本质上和等腰直角三角形半角模型差不多,但因为处于正方形中,所以又有不同。
“K”字形模型
GH2=BG2+DH2(同等腰直角三角形半角模型)
BE+DF=EF
BE=NE,DF=NF,AE平分∠BEF,AF平分∠AFE
(5)矩形半角模型
方法一:补成正方形半角模型,结合相似解答。
方法二:补成“K”字形模型,利用直角三角形全等,结合相似解答。
5、“K”字形模型(一线三等角)
基本思路:利用三个相等的角寻找全等或相似。
(1)全等
△ABC≌△DCE
(2)相似
△ABC∽△DCE→AC·CD=AB·DE
6、燕尾模型
基本思路:将面积与边联系起来。
7、四点共圆模型
基本思路:利用圆的性质转换相等的角。
(1)定长对定角型(蝴蝶型(反“8”型)相似)
以定长为弦,定角为圆周角作圆(三点共圆,由于定角的顶点为动点,由三点共圆引出四点共圆、多点共圆)
锐角
相交弦定理:AE·DE=BE·CE(△ACE∽△BDE可证)
钝角
直角
当定角分别为一些特殊角时,如30°,45°,60°,90°,120°,135°,150°时,可以求出定圆半径与定长的数量关系。不难发现30°和150°、45°和135°、60°和120°,数量关系是一样的。
r=AB
r=AB
r=AB
r=AB
(2)对角互补型
四点共圆?对角互补
托勒密定理:AC·BD=AB·CD+AD·BC
△ABC∽△AED→=
,AC·ED=AD·BC①
△ABE∽△ACD→=
,AC·BE=AB·CD②
①+②即可证。
若AB∥CD,则△ABE∽△DCE(“A”型相似)
若AD∥BC,则△ADE∽△CBE(“8”型相似)
AE·DE=BE·CE(反“A”型相似,△ABE∽△CDE)
若BC为切线,则BC2=AC·CD(母子型相似,△ABC∽△BDC)
(3)特殊型
邻边相等
AB=AC,I为△BCD内心,则有AI=AB=AC。
邻边相等且夹角为60°(等边三角形)
共斜边的等腰直角三角形和普通直角三角形
1、角平分线模型
基本思路:利用角平分线的性质。
(1)三角形内角、外角平分线
OB、OC分别平分∠ABC和∠ACB,则∠O=90°+∠A。
BD、CD为△ABC的外角平分线,则∠D=90°-∠A。
BD平分∠ABC,CD为△ABC的外角平分线,则∠D=∠A。
(2)三角形内心
对任意三角形,有S△ABC=(AB+BC+AC)·r。
对等边三角形,有===。
对直角三角形,有r=(AB+BC-AC)。
2、线段和、差最值模型
基本思路:①两点之间线段最短;
②点到直线距离垂线段最短;
③利用了三角形三边的关系,两边之和大于第三边,两边之差小于第三边,三点共线时取等号。
(1)
点A、B为定点,在直线上找一点P,使得AP+BP的值最小。
(2)
点A、B为定点,在直线上找一点P,使得|AP-BP|的值最大。
(3)
点A、B为定点,在直线上找一点P,使得AP+BP的值最小。
(4)点A、B为定点,在直线上找一点P,使得|AP-BP|的值最大。
(5)
(6)
(7)
(8)
(9)
(10)费马点:①若△ABC内角都小于120°,则能在△ABC内找一点P,使PA+PB+PC的值最小。
②若△ABC有一个内角不小于120°,则△ABC内使PA+PB+PC的值最小的点
P就在钝角所在顶点。
(11)
圆所有的弦中,直径最长。
(12)点P为圆外一定点,点Q为圆上一动点,则PB≤PQ≤PA。
3、旋转模型
基本思路:利用旋转图形的性质。
(1)等腰三角形旋转(两个顶角相等的等腰三角形顶角重合,其中一个三角形绕顶点旋转。)
无论什么三角形,均有△ABD≌△ACE。
(2)正方形旋转
4、半角模型
基本思路:旋转后找全等或相似,利用好含特殊角(30°、45°、60°)的直角三角形边之间的关系。
(1)等腰直角三角形半角模型
MN2=BM2+CN2
(2)顶角为120°等腰三角形半角模型
BM2+NC2-MN2=BM×NC(余弦定理)
一般来说,BM、MN、NC没有特定的关系,当BM:MN:NC=2::1时,∠BDM=90°。
(3)等边三角形与顶角为120°等腰三角形半角模型
BE+CF=EF
(4)正方形半角模型
本质上和等腰直角三角形半角模型差不多,但因为处于正方形中,所以又有不同。
“K”字形模型
GH2=BG2+DH2(同等腰直角三角形半角模型)
BE+DF=EF
BE=NE,DF=NF,AE平分∠BEF,AF平分∠AFE
(5)矩形半角模型
方法一:补成正方形半角模型,结合相似解答。
方法二:补成“K”字形模型,利用直角三角形全等,结合相似解答。
5、“K”字形模型(一线三等角)
基本思路:利用三个相等的角寻找全等或相似。
(1)全等
△ABC≌△DCE
(2)相似
△ABC∽△DCE→AC·CD=AB·DE
6、燕尾模型
基本思路:将面积与边联系起来。
7、四点共圆模型
基本思路:利用圆的性质转换相等的角。
(1)定长对定角型(蝴蝶型(反“8”型)相似)
以定长为弦,定角为圆周角作圆(三点共圆,由于定角的顶点为动点,由三点共圆引出四点共圆、多点共圆)
锐角
相交弦定理:AE·DE=BE·CE(△ACE∽△BDE可证)
钝角
直角
当定角分别为一些特殊角时,如30°,45°,60°,90°,120°,135°,150°时,可以求出定圆半径与定长的数量关系。不难发现30°和150°、45°和135°、60°和120°,数量关系是一样的。
r=AB
r=AB
r=AB
r=AB
(2)对角互补型
四点共圆?对角互补
托勒密定理:AC·BD=AB·CD+AD·BC
△ABC∽△AED→=
,AC·ED=AD·BC①
△ABE∽△ACD→=
,AC·BE=AB·CD②
①+②即可证。
若AB∥CD,则△ABE∽△DCE(“A”型相似)
若AD∥BC,则△ADE∽△CBE(“8”型相似)
AE·DE=BE·CE(反“A”型相似,△ABE∽△CDE)
若BC为切线,则BC2=AC·CD(母子型相似,△ABC∽△BDC)
(3)特殊型
邻边相等
AB=AC,I为△BCD内心,则有AI=AB=AC。
邻边相等且夹角为60°(等边三角形)
共斜边的等腰直角三角形和普通直角三角形
同课章节目录
