有理数的乘方课件

(共16张PPT)
创设情境
对折1次有____层
对折2次有____层
对折3次有____层
对折4次有____层
对折5次有____层
2
2×2
2×2×2
2×2×2×2
2×2×2×2×2
我们用一张纸进行对折，再对折……，并探讨对折的次数与纸的层数的关系。
7
7
面积
体积
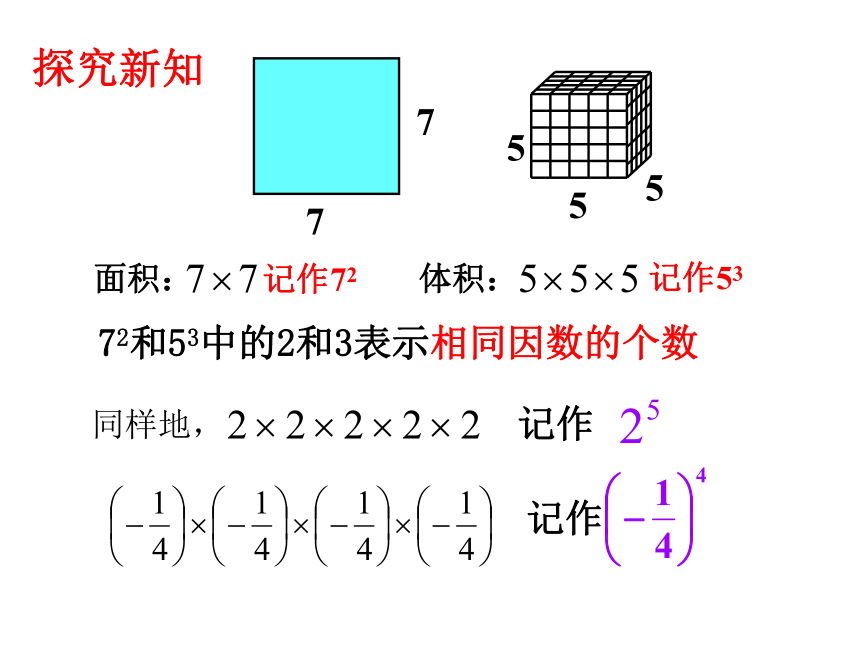
面积：
体积：
记作72
记作53
记作
72和53中的2和3表示相同因数的个数
探究新知
同样地，
记作
5
5
5
a·a·a· … ·a
n个a
说出这些算式各有什么特点？
特点：1.乘法运算 2.每个因数都相同
底数
指数
幂
an
求几个相同因数的积的运算叫做乘方，
n个a
a·a·a· … ·a
概念
乘方的结果叫做幂。
= an
读作：a的n次方或a的n次幂.
意义：代表n个a相乘.



加法
和
减法
差
乘法
积
除法
商
乘方
幂
运算
结果
1）在1210中，12是 数，10是 数，
读作 ；
2） 的底数是 ，指数是 ，
读作 ；
7
的7次方或
底
指
12的10次方或12的10次幂
的7次幂
3）如果把5看成乘方，那么底数是 ，
指数是 ，可读作 ;
5
1
5的一次方或5的一次幂
试试你的身手(一)
把下列乘法算式写成乘方的形式：
1、1×1×1×1×1×1×1= ；
2、3×3×3×3×3= ；
3、(－3)×(－3)×(－3)×(－3) = ；
4、
注意问题：
当底数是负数或分数时，写成乘方的形式，底数须加括号.
试试你的身手(二)
=
例1：说出下列各式的意义，并计算：
（1）(-4)3 （2） ;
解:（1）(-4)3=
=
(-4)×(-4)×(-4)
=-64
（2） =
× × ×
22 23 34 (－2)2 (－2)3 (－3)3
计算结果
底数的符号
指数奇偶性
幂的符号
试一试，请填下表
正
正
正
负
负
负
偶
奇
偶
偶
奇
奇
正
正
正
正
负
负
合作探究
正数的几次幂是正数？负数的几次幂是正数？负数的几次幂是负数？
幂的符号法则：
（1）正数的任何次幂是正数；
（2）负数的偶次幂是正数；负数的奇次幂
是负数；
（3）0的正整数次幂等于零；
4
8
81
4
-8
-27
-34的底数是3，表示3的4次方的相反数。
（-3)4与-34 有什么区别？
(-3)4的底数是-3，表示4个–3相乘。
探索交流
拓展提高：计算
（1）
（3）
（5）1201
（4） 43
（6）
-1
（2）
(
)
2
3
-
9
-125
64
1
- —
81
1
归纳小结
今天我们学习了什么内容？你有哪些收获？
一种运算—乘方
两个注意—当底数是分数或负数时，
表示乘方时要加括号；
幂的符号法则
三个概念—底数，指数，幂.
课堂检测
1. 叫做乘方，
。 叫做幂.
2.在(-4)4中，底数是 ，指数是 ，
意义是 .
3.计算：
(1)25 (2)43 (3) - 0.13 (4)
求几个相同因数的积的运算
乘方的结果
-4
4
4个-4相乘
32
64
-0.001
1
64
作业：
课本P65 习题A组1、2
再 见