多边形复习1
图片预览

文档简介
(共19张PPT)
多边形的复习(一)
——三角形
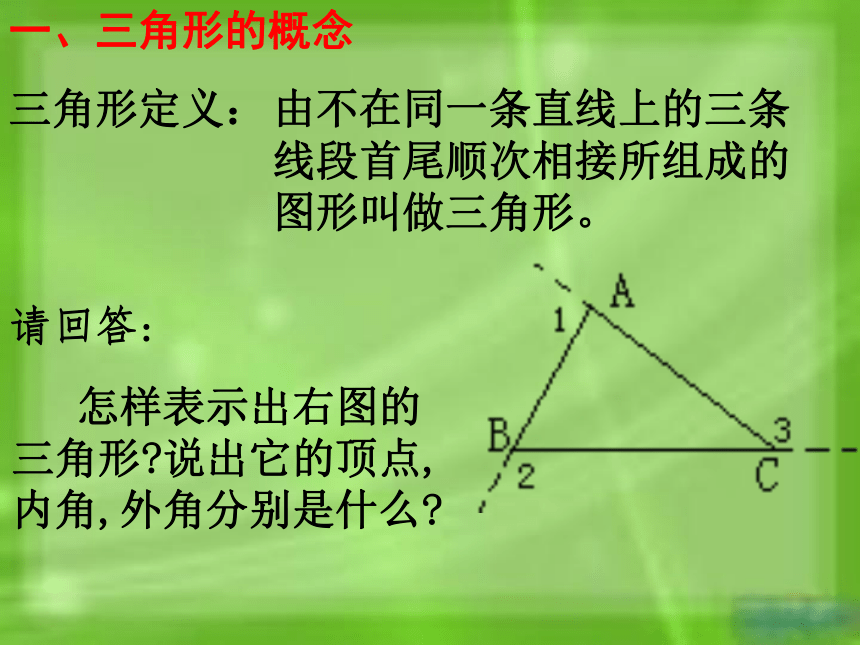
由不在同一条直线上的三条
线段首尾顺次相接所组成的
图形叫做三角形。
一、三角形的概念
三角形定义:
请回答:
怎样表示出右图的
三角形 说出它的顶点,
内角,外角分别是什么
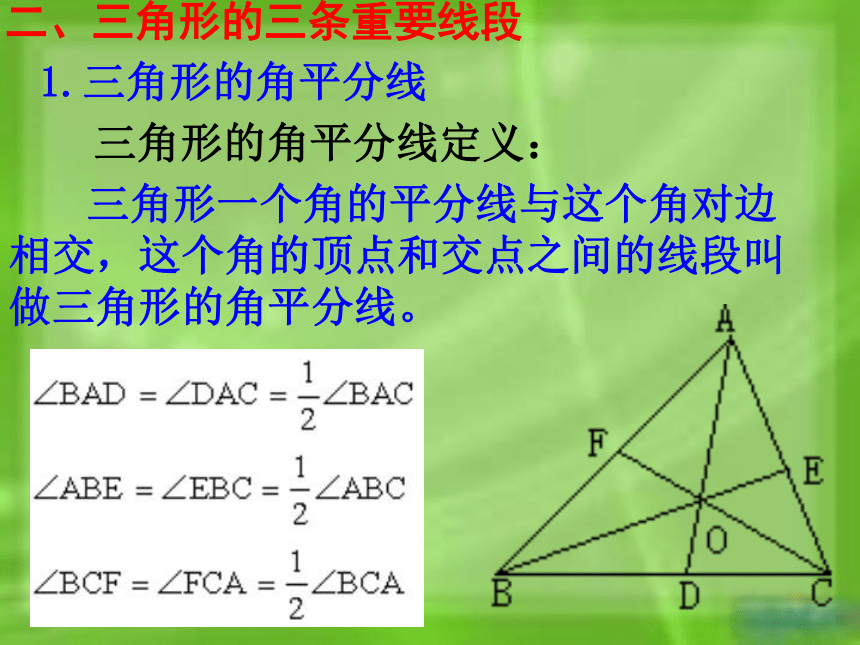
三角形一个角的平分线与这个角对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
二、三角形的三条重要线段
1.三角形的角平分线
三角形的角平分线定义:
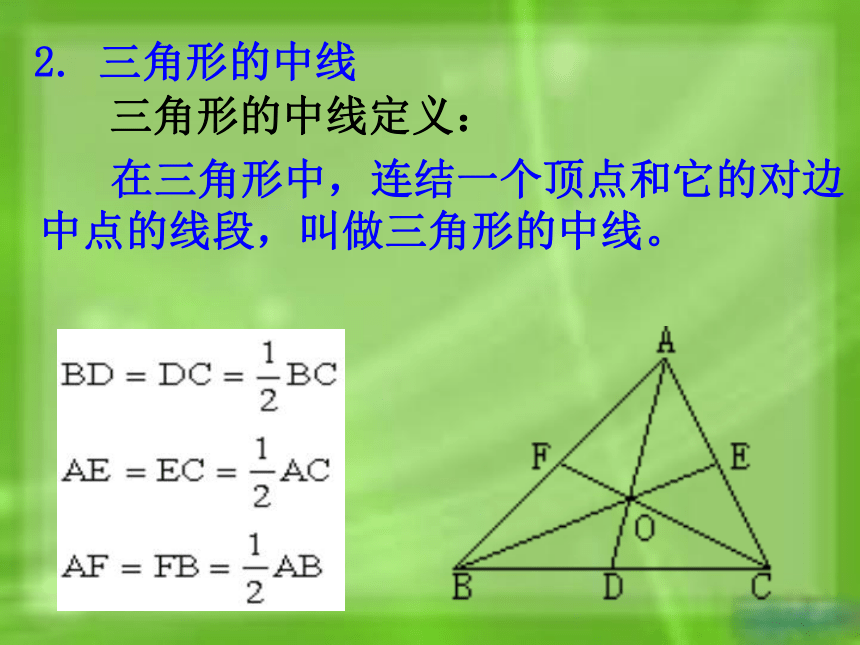
2. 三角形的中线
三角形的中线定义:
在三角形中,连结一个顶点和它的对边
中点的线段,叫做三角形的中线。
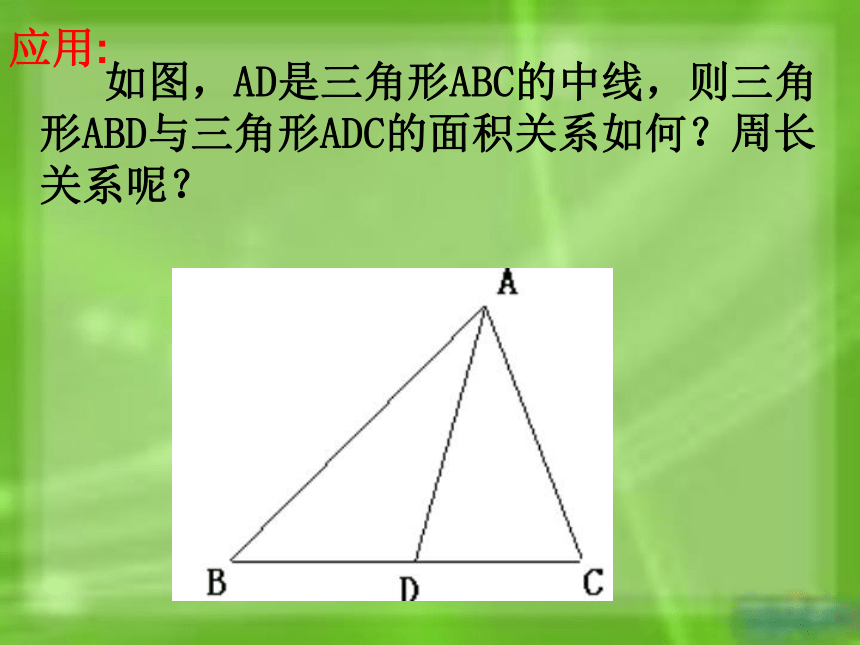
如图,AD是三角形ABC的中线,则三角形ABD与三角形ADC的面积关系如何?周长关系呢?
应用:
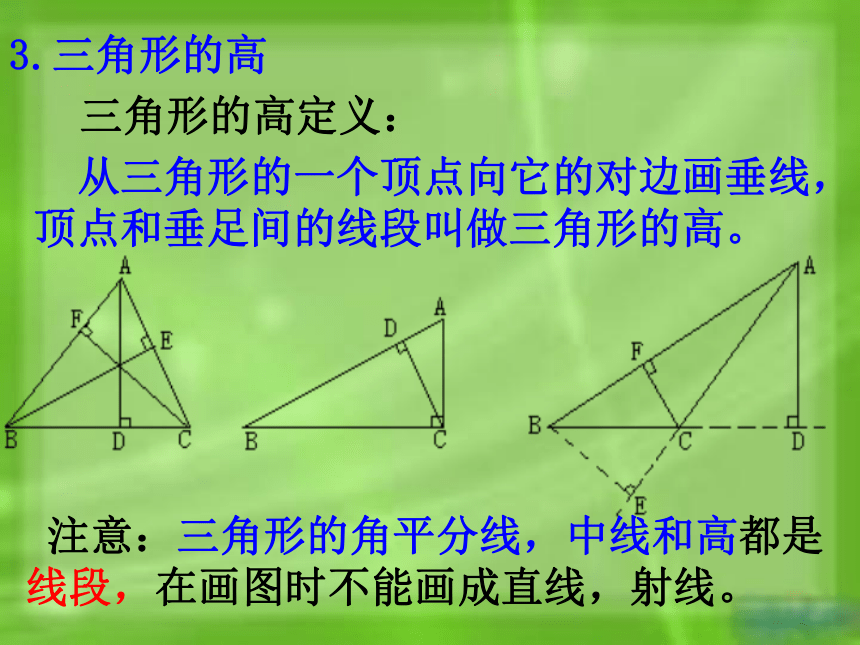
从三角形的一个顶点向它的对边画垂线,
顶点和垂足间的线段叫做三角形的高。
3.三角形的高
三角形的高定义:
注意:三角形的角平分线,中线和高都是
线段,在画图时不能画成直线,射线。
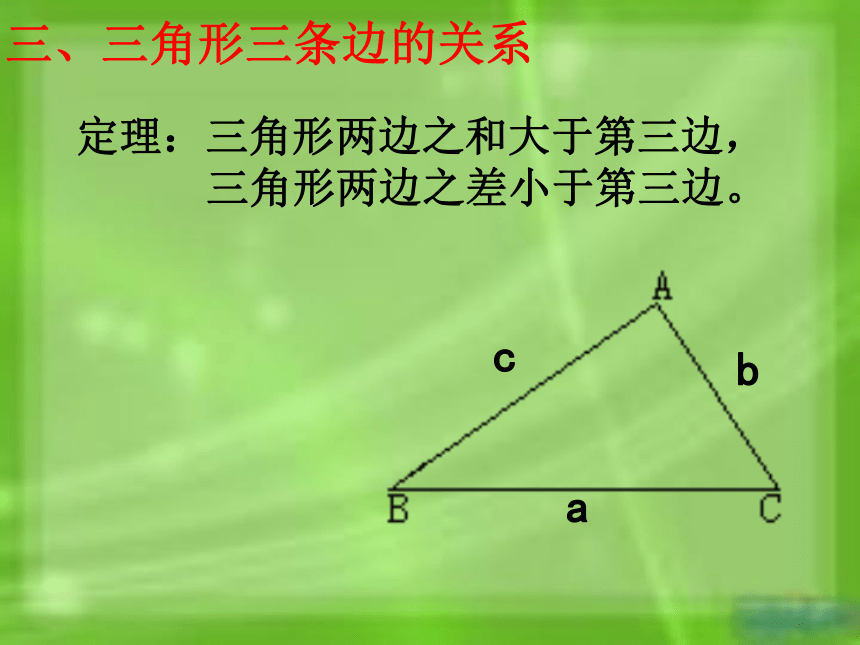
三、三角形三条边的关系
定理:三角形两边之和大于第三边,
三角形两边之差小于第三边。
a
b
c
2.三角形内角和定理推论: 直角三角形的两个锐角互余.
如图在△ABC中,∠C=90°那么∠A+∠B=90°
四、三角形的内角和
1.三角形内角和定理:
三角形三个内角的和等于180°。
3.三角形的一个外角等于和它不相邻的两个内角的和。
即:如图∠ACD是△ABC的一个外角,
那么∠ACD=∠A+∠B。
如图:AD与BC相交于点O,
则∠A+∠C=∠B+∠D。
4.三角形的一个外角大于任何一个和
它不相邻的内角。即:
如图∠ACD是△ABC的一个外角,
那么∠ACD>∠A,∠ACD>∠B。
重要图形:在下列三角形ABC中,BO与CO分别是角平分线,∠BOC与∠A有何关系?
图(1)
图(2)
图(3)
应用:
关于三角形的内角(或外角)平分线有如下的结论:
(1)
(2)
(3)
A
B
C
P
A
B
C
D
E
P
A
B
D
C
P
(两内角平分线)
(两外角平分线)
(一内角、一外角平分线)
(1)若∠A=44°,则∠BPC=___。
(2)若∠A=50°,则∠P= 。
(3)若∠A=70°,则∠P= 。
如图:CD是三角形ABC的外角平分线,
说明∠BAC>∠B.
等腰三角形的周长20,一边长5,则另两边长为 。
等腰三角形的腰长6,求底边a的范围和周长L的范围
等腰三角形的底边长4,求腰长x的范围
过n边形一个顶点连对角线,可以得
(n-3)条对角线,并且将n边形分成
(n-2)个三角形,这(n-2)个三角形
的内角和恰好是
多边形的内角和=(n-2)·180°。
五、多边形内角和定理
六、多边形的外角和定理
1、多边形的每个内角与它相邻的外角是
邻补角,所以n边形内角和加外角和等于
n·180°,
外角和=n·180°-(n-2)·180°
=360°
2、多边形外角和定理:任意多边形的
外角和等于360°.
注意:
n边形的外角和恒等于360°,它与
边数的多少无关.
七、用形状、大小完全相同的一种或几种
平面图形进行拼接,彼此之间不留空隙、
不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
1.用形状相同的三角形或四边形能铺满地面。
2.若用两种正多边形铺满地面,则有以下
几种组合:正三与正四、正三与正六、
正四与正八…
3. 若用三种正多边形铺满地面,则有以下
几种组合:正三、正四与正六,…
多边形的复习(一)
——三角形
由不在同一条直线上的三条
线段首尾顺次相接所组成的
图形叫做三角形。
一、三角形的概念
三角形定义:
请回答:
怎样表示出右图的
三角形 说出它的顶点,
内角,外角分别是什么
三角形一个角的平分线与这个角对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
二、三角形的三条重要线段
1.三角形的角平分线
三角形的角平分线定义:
2. 三角形的中线
三角形的中线定义:
在三角形中,连结一个顶点和它的对边
中点的线段,叫做三角形的中线。
如图,AD是三角形ABC的中线,则三角形ABD与三角形ADC的面积关系如何?周长关系呢?
应用:
从三角形的一个顶点向它的对边画垂线,
顶点和垂足间的线段叫做三角形的高。
3.三角形的高
三角形的高定义:
注意:三角形的角平分线,中线和高都是
线段,在画图时不能画成直线,射线。
三、三角形三条边的关系
定理:三角形两边之和大于第三边,
三角形两边之差小于第三边。
a
b
c
2.三角形内角和定理推论: 直角三角形的两个锐角互余.
如图在△ABC中,∠C=90°那么∠A+∠B=90°
四、三角形的内角和
1.三角形内角和定理:
三角形三个内角的和等于180°。
3.三角形的一个外角等于和它不相邻的两个内角的和。
即:如图∠ACD是△ABC的一个外角,
那么∠ACD=∠A+∠B。
如图:AD与BC相交于点O,
则∠A+∠C=∠B+∠D。
4.三角形的一个外角大于任何一个和
它不相邻的内角。即:
如图∠ACD是△ABC的一个外角,
那么∠ACD>∠A,∠ACD>∠B。
重要图形:在下列三角形ABC中,BO与CO分别是角平分线,∠BOC与∠A有何关系?
图(1)
图(2)
图(3)
应用:
关于三角形的内角(或外角)平分线有如下的结论:
(1)
(2)
(3)
A
B
C
P
A
B
C
D
E
P
A
B
D
C
P
(两内角平分线)
(两外角平分线)
(一内角、一外角平分线)
(1)若∠A=44°,则∠BPC=___。
(2)若∠A=50°,则∠P= 。
(3)若∠A=70°,则∠P= 。
如图:CD是三角形ABC的外角平分线,
说明∠BAC>∠B.
等腰三角形的周长20,一边长5,则另两边长为 。
等腰三角形的腰长6,求底边a的范围和周长L的范围
等腰三角形的底边长4,求腰长x的范围
过n边形一个顶点连对角线,可以得
(n-3)条对角线,并且将n边形分成
(n-2)个三角形,这(n-2)个三角形
的内角和恰好是
多边形的内角和=(n-2)·180°。
五、多边形内角和定理
六、多边形的外角和定理
1、多边形的每个内角与它相邻的外角是
邻补角,所以n边形内角和加外角和等于
n·180°,
外角和=n·180°-(n-2)·180°
=360°
2、多边形外角和定理:任意多边形的
外角和等于360°.
注意:
n边形的外角和恒等于360°,它与
边数的多少无关.
七、用形状、大小完全相同的一种或几种
平面图形进行拼接,彼此之间不留空隙、
不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
1.用形状相同的三角形或四边形能铺满地面。
2.若用两种正多边形铺满地面,则有以下
几种组合:正三与正四、正三与正六、
正四与正八…
3. 若用三种正多边形铺满地面,则有以下
几种组合:正三、正四与正六,…
