八年级下19.2.3正方形的性质
文档属性
| 名称 | 八年级下19.2.3正方形的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-27 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
“在学习中要敢于做减法,就是减去前人已经解决的部分,看看还有那些问题没有解决,需要我们去探索解决。”
——华罗庚
请同学们画一个四边形,
要求它既是矩形又是菱形。
19.2 正方形的性质
活动一 我的学习,我做主 (自学课本100 页内容)
学习目标
1、掌握正方形的概念,以及正方形与平行四边形、矩形、
菱形的关系。
2、根据正方形与平行四边形、矩形、菱形的关系探索并
掌握正方形的性质,并运用正方形的性质解决一些问题,
培养我们的合情推理能力。
3、通过正方形的学习,体会知识之间的相互联系与区别,
感受数 学之美培养我们的自学能力。
活动二 学有所获
通过自学我知道了……
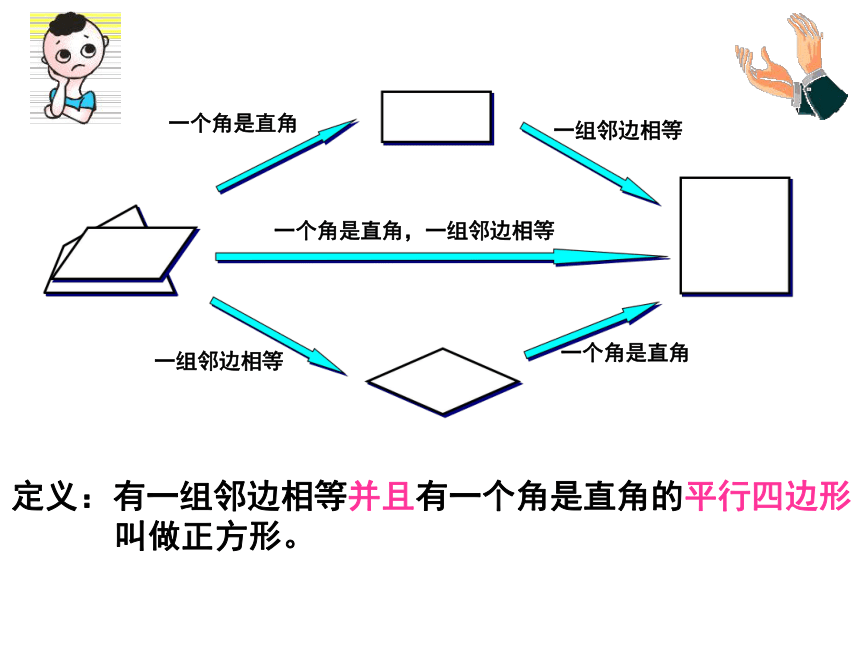
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形。
一个角是直角
一个角是直角
一个角是直角,一组邻边相等
一组邻边相等
一组邻边相等
平行四边形
矩形
菱形
正方形
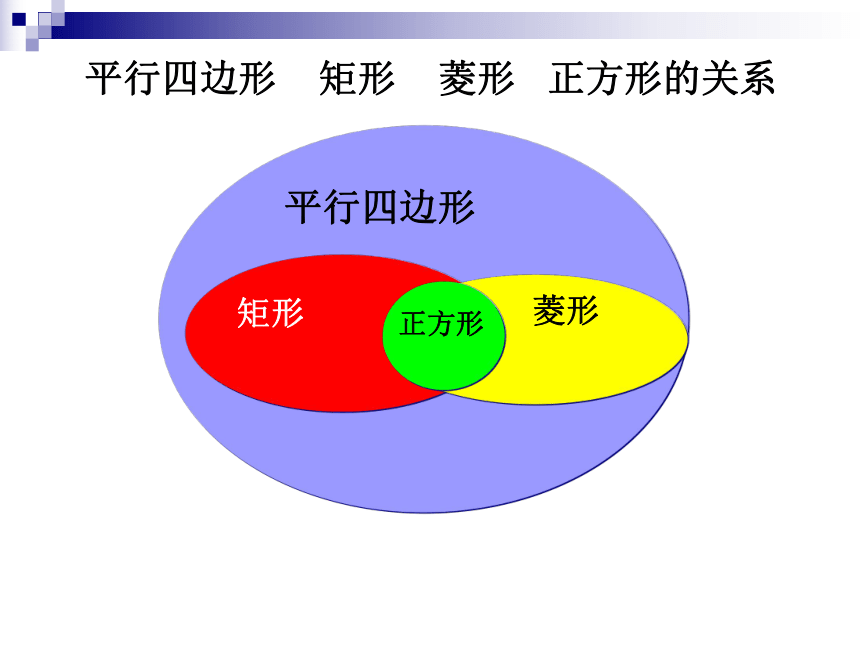
平行四边形 矩形 菱形 正方形的关系
正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
活动三 学以致用
一、精心选一选
1、正方形具有而菱形不具有的性质是( )
A、四边都相等
B、每一条对角线平分一组对角
C、对角线互相平分且相等
D、对角相等邻角互补
2、正方形和矩形都具有的性质是( )
A、对角线互相垂直且相等
B、对边平行且邻边相等
C、对角线相等且每一条对角线平分一组对角
D、四个角都相等,对角线相等,对边平行。
C
D
二、耐心填一填
1、已知正方形的一条对角线长为4cm,则这个正方形的周长是______cm。面积是_________。
2、已知正方形ABCD的边长为4,E、F分别是BC和CD边上的中点,则 △AEF的面积是________
活动三 学以致用
A
B
C
D
E
F
8cm2
6cm2
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
题型练习如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗?通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
活动四 畅所欲言 谈收获
这节课我学会了……
这节课我知道了…………
这节课我想提醒同学们…………
这节课我知道了学习要…………
这节课我想对老师说………………
这节课我感受到数学这门学科………………
拓展延伸
1、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
题型练习.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 ____=___
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
MD
FD
自学检测
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
“在学习中要敢于做减法,就是减去前人已经解决的部分,看看还有那些问题没有解决,需要我们去探索解决。”
——华罗庚
请同学们画一个四边形,
要求它既是矩形又是菱形。
19.2 正方形的性质
活动一 我的学习,我做主 (自学课本100 页内容)
学习目标
1、掌握正方形的概念,以及正方形与平行四边形、矩形、
菱形的关系。
2、根据正方形与平行四边形、矩形、菱形的关系探索并
掌握正方形的性质,并运用正方形的性质解决一些问题,
培养我们的合情推理能力。
3、通过正方形的学习,体会知识之间的相互联系与区别,
感受数 学之美培养我们的自学能力。
活动二 学有所获
通过自学我知道了……
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形。
一个角是直角
一个角是直角
一个角是直角,一组邻边相等
一组邻边相等
一组邻边相等
平行四边形
矩形
菱形
正方形
平行四边形 矩形 菱形 正方形的关系
正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
活动三 学以致用
一、精心选一选
1、正方形具有而菱形不具有的性质是( )
A、四边都相等
B、每一条对角线平分一组对角
C、对角线互相平分且相等
D、对角相等邻角互补
2、正方形和矩形都具有的性质是( )
A、对角线互相垂直且相等
B、对边平行且邻边相等
C、对角线相等且每一条对角线平分一组对角
D、四个角都相等,对角线相等,对边平行。
C
D
二、耐心填一填
1、已知正方形的一条对角线长为4cm,则这个正方形的周长是______cm。面积是_________。
2、已知正方形ABCD的边长为4,E、F分别是BC和CD边上的中点,则 △AEF的面积是________
活动三 学以致用
A
B
C
D
E
F
8cm2
6cm2
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
题型练习如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗?通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
活动四 畅所欲言 谈收获
这节课我学会了……
这节课我知道了…………
这节课我想提醒同学们…………
这节课我知道了学习要…………
这节课我想对老师说………………
这节课我感受到数学这门学科………………
拓展延伸
1、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
题型练习.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 ____=___
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
MD
FD
自学检测
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
