北师大版七年级数学下册 第五章生活中的轴对称综合测评含答案
文档属性
| 名称 | 北师大版七年级数学下册 第五章生活中的轴对称综合测评含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 259.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 11:09:04 | ||
图片预览

文档简介
生活中的轴对称综合测评(
(满分:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.花窗是中国古代园林建筑中窗的一种装饰和美化的形式,既具备实用功能,又带有装饰效应.下列各个窗户不是轴对称图形的是
(
)
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”图案中,是轴对称图形的为( )
A.
B.
C.
D.
2.图1是第21届夏季奥林匹克运动会会徽,会徽中的图案为轴对称图形,它的对称轴有
(
)
A.1条
B.2条
C.
3条
D.
4条
3.下列图形中,关于直线l对称的是( )
A
B
C
D
4.如图
2,在△ABC中,AB=AC,CB=CD,若∠A=40°,则∠BDC的度数为
(
)
A.
40°
B.
45°
C.
55°
D.
70°
5.下列说法正确的是
(
)
A.过线段中点的直线是该线段的对称轴
B.
成轴对称的两条线段一定相等
C.两条相等的线段一定关于某条直线成轴对称
D.
线段不一定是轴对称图形
6.如图3,在△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC,若AB=3,BC=4,AC=5,则CD+DE的长为(
)
(
)
A.
3
B.
4
C.
5
D.
6
7.
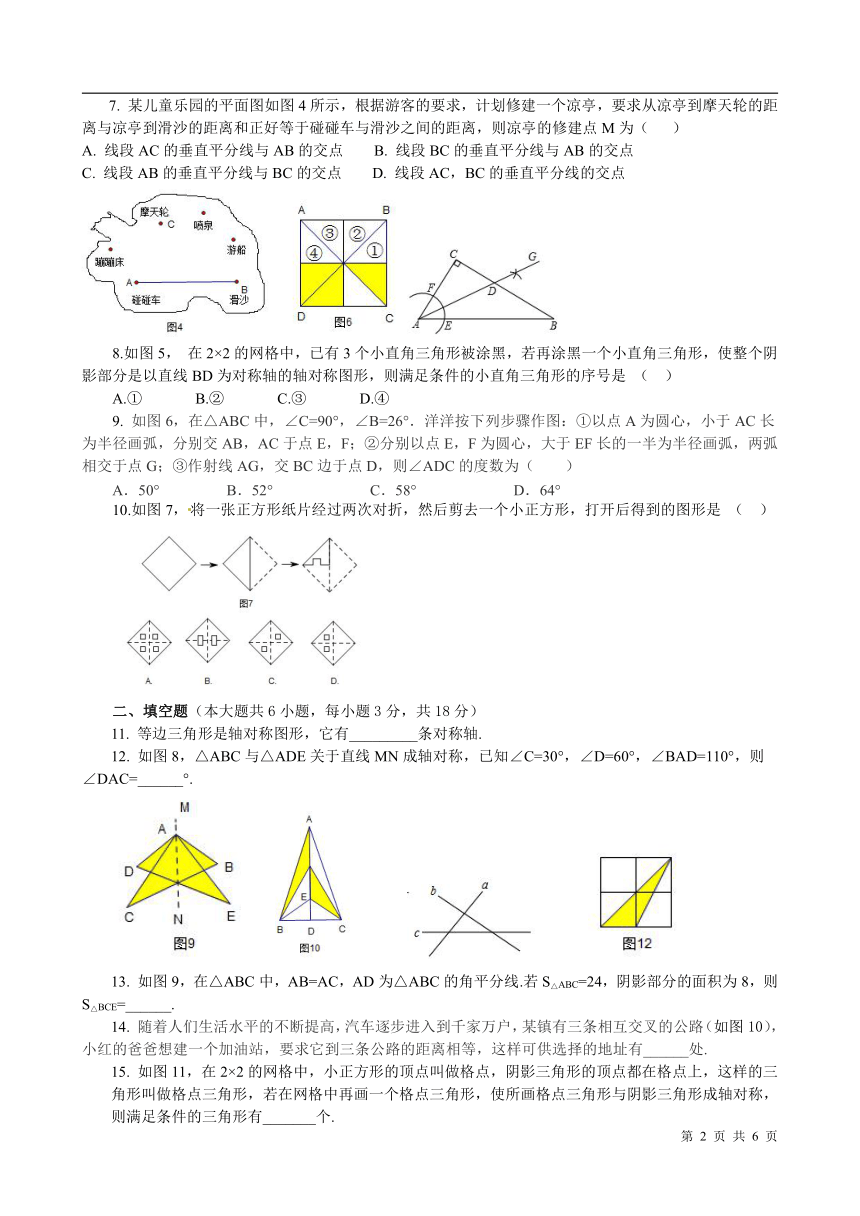
某儿童乐园的平面图如图4所示,根据游客的要求,计划修建一个凉亭,要求从凉亭到摩天轮的距离与凉亭到滑沙的距离和正好等于碰碰车与滑沙之间的距离,则凉亭的修建点M为(
)
A.
线段AC的垂直平分线与AB的交点
B.
线段BC的垂直平分线与AB的交点
C.
线段AB的垂直平分线与BC的交点
D.
线段AC,BC的垂直平分线的交点
8.如图5,
在2×2的网格中,已有3个小直角三角形被涂黑,若再涂黑一个小直角三角形,使整个阴影部分是以直线BD为对称轴的轴对称图形,则满足条件的小直角三角形的序号是
(
)
A.①
B.②
C.③
D.④
9.
如图6,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A.50°
B.52°
C.58°
D.64°
10.如图7,将一张正方形纸片经过两次对折,然后剪去一个小正方形,打开后得到的图形是
(
)
二、填空题(本大题共6小题,每小题3分,共18分)
11.
等边三角形是轴对称图形,它有_________条对称轴.
12.
如图8,△ABC与△ADE关于直线MN成轴对称,已知∠C=30°,∠D=60°,∠BAD=110°,则∠DAC=______°.
如图9,在△ABC中,AB=AC,AD为△ABC的角平分线.若S△ABC=24,阴影部分的面积为8,则S△BCE=______.
随着人们生活水平的不断提高,汽车逐步进入到千家万户,某镇有三条相互交叉的公路(如图10),小红的爸爸想建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有______处.
15.
如图11,在2×2的网格中,小正方形的顶点叫做格点,阴影三角形的顶点都在格点上,这样的三角形叫做格点三角形,若在网格中再画一个格点三角形,使所画格点三角形与阴影三角形成轴对称,则满足条件的三角形有_______个.
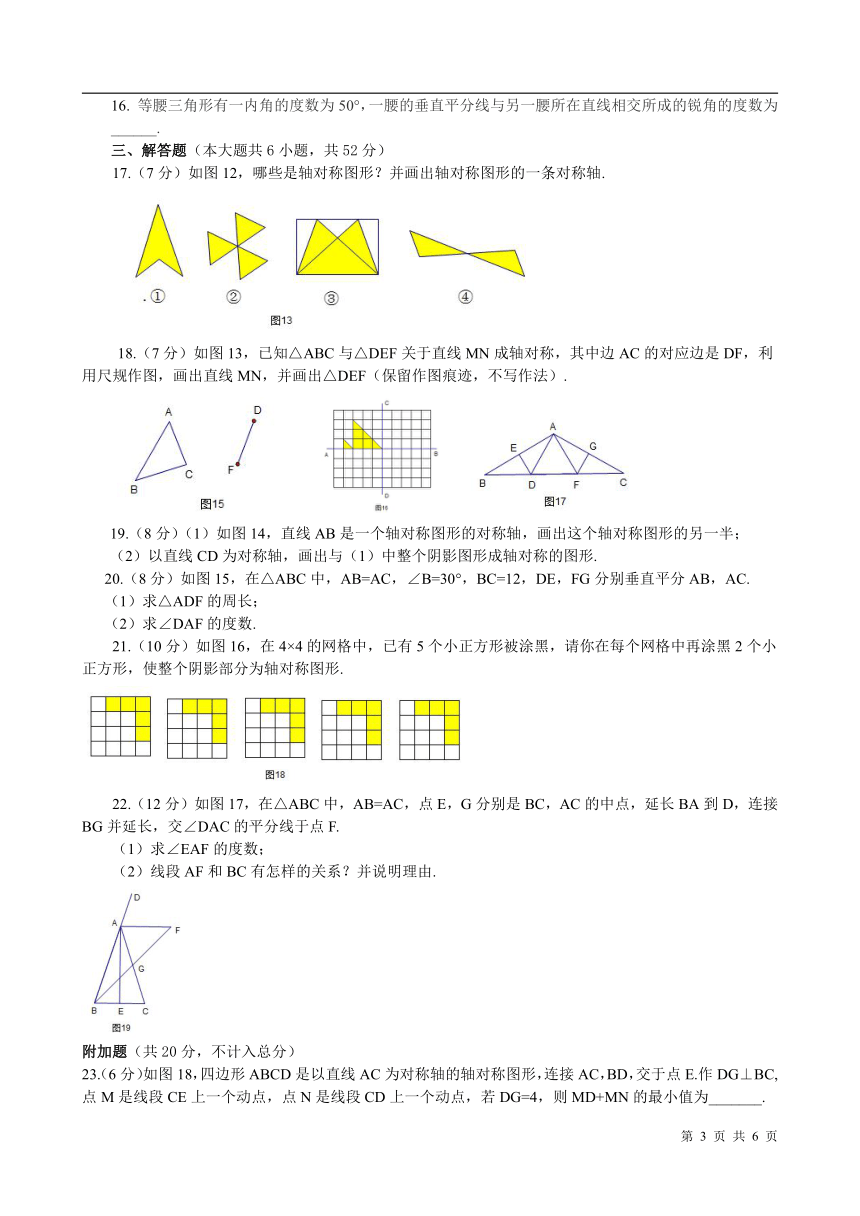
16.
等腰三角形有一内角的度数为50°,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为
______.
三、解答题(本大题共6小题,共52分)
17.(7分)如图12,哪些是轴对称图形?并画出轴对称图形的一条对称轴.
18.(7分)如图13,已知△ABC与△DEF关于直线MN成轴对称,其中边AC的对应边是DF,利用尺规作图,画出直线MN,并画出△DEF(保留作图痕迹,不写作法).
19.(8分)(1)如图14,直线AB是一个轴对称图形的对称轴,画出这个轴对称图形的另一半;
(2)以直线CD为对称轴,画出与(1)中整个阴影图形成轴对称的图形.
20.(8分)如图15,在△ABC中,AB=AC,∠B=30°,BC=12,DE,FG分别垂直平分AB,AC.
(1)求△ADF的周长;
(2)求∠DAF的度数.
21.(10分)如图16,在4×4的网格中,已有5个小正方形被涂黑,请你在每个网格中再涂黑2个小正方形,使整个阴影部分为轴对称图形.
22.(12分)如图17,在△ABC中,AB=AC,点E,G分别是BC,AC的中点,延长BA到D,连接BG并延长,交∠DAC的平分线于点F.
(1)求∠EAF的度数;
(2)线段AF和BC有怎样的关系?并说明理由.
附加题(共20分,不计入总分)
23.(6分)如图18,四边形ABCD是以直线AC为对称轴的轴对称图形,连接AC,BD,交于点E.作DG⊥BC,点M是线段CE上一个动点,点N是线段CD上一个动点,若DG=4,则MD+MN的最小值为_______.
24.(14分)如图19,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M,N,使得△PMN的周长最短.若能,请画出点M,N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.
生活中的轴对称综合测评
参考答案
一、1.
B
2.
A
3.
C
4.
C
5.
B
6.
B
7.
A
8.
C
9.
C
10.
B
二、11.
3
12.
20
13.
8
14.
4
15.
4
16.
40°或10°
三、17.
解:轴对称图形有①②③,画对称轴略.
解:如图1所示.
解:如图2所示.
20.解:(1)因为DE,FG分别垂直平分AB,AC,所以AD=BD,AF=CF.
所以AD+AF+DF=BD+DF+CF=BC=12.所以△ADF的周长为12.
(2)因为AB=AC,∠B=30°,所以∠B=∠C=30°,所以∠BAC=120°.
因为AD=BD,AF=CF,所以∠BAD=∠B=30°,∠CAF=∠C=30°.
所以∠DAF=∠BAC-∠BAD-∠CAF=120°-30°-30°=60°.
21.
答案不唯一,合理即可,如图3所示.
22.解:(1)因为AB=AC,点E是BC的中点,所以∠CAE=∠BAC.
因为AF平分∠DAC,所以∠CAF=∠DAC.
所以∠EAF=∠CAE+∠CAF=(∠BAC+∠DAC)=∠BAD=×180°=90°.
(2)AF∥BC,AF=BC.理由如下:
因为AB=AC,点E是BC的中点,所以AE⊥BC.所以∠AEC=90°.
因为∠EAF=90°,所以∠AEC+∠EAF=180°.所以AF∥BC.所以∠FAG=∠C.
因为AG=CG,∠AGF=∠CGB,所以△AFG≌△CBG.所以AF=BC.
4
解:存在,如图4,点M,N即为所求.
(2)因为∠ACB=40°,所以∠CMN+∠CNM=180°-40°=140°.
根据轴对称的性质,得∠PMA=∠AMP',∠PNB=∠BNP''.
因为∠AMP'=∠CMN,∠BNP''=∠CNM,所以2(∠PMA+∠PNB)=280°.
所以∠PMN+∠PNM=360°-280°=80°.所以∠MPN=180°-(∠PMN+∠PNM)=100°.
第
6
页
共
8
页
(满分:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.花窗是中国古代园林建筑中窗的一种装饰和美化的形式,既具备实用功能,又带有装饰效应.下列各个窗户不是轴对称图形的是
(
)
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”图案中,是轴对称图形的为( )
A.
B.
C.
D.
2.图1是第21届夏季奥林匹克运动会会徽,会徽中的图案为轴对称图形,它的对称轴有
(
)
A.1条
B.2条
C.
3条
D.
4条
3.下列图形中,关于直线l对称的是( )
A
B
C
D
4.如图
2,在△ABC中,AB=AC,CB=CD,若∠A=40°,则∠BDC的度数为
(
)
A.
40°
B.
45°
C.
55°
D.
70°
5.下列说法正确的是
(
)
A.过线段中点的直线是该线段的对称轴
B.
成轴对称的两条线段一定相等
C.两条相等的线段一定关于某条直线成轴对称
D.
线段不一定是轴对称图形
6.如图3,在△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC,若AB=3,BC=4,AC=5,则CD+DE的长为(
)
(
)
A.
3
B.
4
C.
5
D.
6
7.
某儿童乐园的平面图如图4所示,根据游客的要求,计划修建一个凉亭,要求从凉亭到摩天轮的距离与凉亭到滑沙的距离和正好等于碰碰车与滑沙之间的距离,则凉亭的修建点M为(
)
A.
线段AC的垂直平分线与AB的交点
B.
线段BC的垂直平分线与AB的交点
C.
线段AB的垂直平分线与BC的交点
D.
线段AC,BC的垂直平分线的交点
8.如图5,
在2×2的网格中,已有3个小直角三角形被涂黑,若再涂黑一个小直角三角形,使整个阴影部分是以直线BD为对称轴的轴对称图形,则满足条件的小直角三角形的序号是
(
)
A.①
B.②
C.③
D.④
9.
如图6,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A.50°
B.52°
C.58°
D.64°
10.如图7,将一张正方形纸片经过两次对折,然后剪去一个小正方形,打开后得到的图形是
(
)
二、填空题(本大题共6小题,每小题3分,共18分)
11.
等边三角形是轴对称图形,它有_________条对称轴.
12.
如图8,△ABC与△ADE关于直线MN成轴对称,已知∠C=30°,∠D=60°,∠BAD=110°,则∠DAC=______°.
如图9,在△ABC中,AB=AC,AD为△ABC的角平分线.若S△ABC=24,阴影部分的面积为8,则S△BCE=______.
随着人们生活水平的不断提高,汽车逐步进入到千家万户,某镇有三条相互交叉的公路(如图10),小红的爸爸想建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有______处.
15.
如图11,在2×2的网格中,小正方形的顶点叫做格点,阴影三角形的顶点都在格点上,这样的三角形叫做格点三角形,若在网格中再画一个格点三角形,使所画格点三角形与阴影三角形成轴对称,则满足条件的三角形有_______个.
16.
等腰三角形有一内角的度数为50°,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为
______.
三、解答题(本大题共6小题,共52分)
17.(7分)如图12,哪些是轴对称图形?并画出轴对称图形的一条对称轴.
18.(7分)如图13,已知△ABC与△DEF关于直线MN成轴对称,其中边AC的对应边是DF,利用尺规作图,画出直线MN,并画出△DEF(保留作图痕迹,不写作法).
19.(8分)(1)如图14,直线AB是一个轴对称图形的对称轴,画出这个轴对称图形的另一半;
(2)以直线CD为对称轴,画出与(1)中整个阴影图形成轴对称的图形.
20.(8分)如图15,在△ABC中,AB=AC,∠B=30°,BC=12,DE,FG分别垂直平分AB,AC.
(1)求△ADF的周长;
(2)求∠DAF的度数.
21.(10分)如图16,在4×4的网格中,已有5个小正方形被涂黑,请你在每个网格中再涂黑2个小正方形,使整个阴影部分为轴对称图形.
22.(12分)如图17,在△ABC中,AB=AC,点E,G分别是BC,AC的中点,延长BA到D,连接BG并延长,交∠DAC的平分线于点F.
(1)求∠EAF的度数;
(2)线段AF和BC有怎样的关系?并说明理由.
附加题(共20分,不计入总分)
23.(6分)如图18,四边形ABCD是以直线AC为对称轴的轴对称图形,连接AC,BD,交于点E.作DG⊥BC,点M是线段CE上一个动点,点N是线段CD上一个动点,若DG=4,则MD+MN的最小值为_______.
24.(14分)如图19,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M,N,使得△PMN的周长最短.若能,请画出点M,N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.
生活中的轴对称综合测评
参考答案
一、1.
B
2.
A
3.
C
4.
C
5.
B
6.
B
7.
A
8.
C
9.
C
10.
B
二、11.
3
12.
20
13.
8
14.
4
15.
4
16.
40°或10°
三、17.
解:轴对称图形有①②③,画对称轴略.
解:如图1所示.
解:如图2所示.
20.解:(1)因为DE,FG分别垂直平分AB,AC,所以AD=BD,AF=CF.
所以AD+AF+DF=BD+DF+CF=BC=12.所以△ADF的周长为12.
(2)因为AB=AC,∠B=30°,所以∠B=∠C=30°,所以∠BAC=120°.
因为AD=BD,AF=CF,所以∠BAD=∠B=30°,∠CAF=∠C=30°.
所以∠DAF=∠BAC-∠BAD-∠CAF=120°-30°-30°=60°.
21.
答案不唯一,合理即可,如图3所示.
22.解:(1)因为AB=AC,点E是BC的中点,所以∠CAE=∠BAC.
因为AF平分∠DAC,所以∠CAF=∠DAC.
所以∠EAF=∠CAE+∠CAF=(∠BAC+∠DAC)=∠BAD=×180°=90°.
(2)AF∥BC,AF=BC.理由如下:
因为AB=AC,点E是BC的中点,所以AE⊥BC.所以∠AEC=90°.
因为∠EAF=90°,所以∠AEC+∠EAF=180°.所以AF∥BC.所以∠FAG=∠C.
因为AG=CG,∠AGF=∠CGB,所以△AFG≌△CBG.所以AF=BC.
4
解:存在,如图4,点M,N即为所求.
(2)因为∠ACB=40°,所以∠CMN+∠CNM=180°-40°=140°.
根据轴对称的性质,得∠PMA=∠AMP',∠PNB=∠BNP''.
因为∠AMP'=∠CMN,∠BNP''=∠CNM,所以2(∠PMA+∠PNB)=280°.
所以∠PMN+∠PNM=360°-280°=80°.所以∠MPN=180°-(∠PMN+∠PNM)=100°.
第
6
页
共
8
页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
