北师大版七年级数学下册第五章生活中的轴对称综合测评含答案
文档属性
| 名称 | 北师大版七年级数学下册第五章生活中的轴对称综合测评含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 260.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 11:13:11 | ||
图片预览

文档简介
第五章
生活中的轴对称综合测评
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1.下列国旗中不是轴对称图形的是
(
)
下列两个图形不是关于某条直线成轴对称的是
(
)
我国传统建筑中,窗框的图案玲珑剔透、千变万化.如图1所示的窗框是一个轴对称图形,其对称轴有
(
)
1条
B.
2条
C.
3条
D.
4条
若等腰三角形的一个内角是80°,则它的底角为
(
)
50°
B.
80°
C.
50°或80°
D.
无法确定
下列判断正确的是
(
)
A.
直角是轴对称图形,对称轴是角平分线
B.
经过线段中点的直线是线段的对称轴
C.
等腰三角形的对称轴是底边上的高
D.
成轴对称的两个三角形一定全等
6.
如图2,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于EF的长为半径作弧,两弧分别交于G,H两点,作直线GH,交EF于点O,连接AO.下列结论正确的是
(
)
A.AO平分∠EAF
B.AO垂直平分EF
C.
GH垂直平分EF
D.GH平分AF
7.
如图3,三条笔直公路两两相交,某石化公司准备在△ABC内修建一个加油站,要求加油站到三条公路的距离相等,则加油站应建在
(
)
AB,AC两边垂直平分线的交点处
B.
AB,AC两边中线的交点处
AB,AC两边高线的交点处
D.∠ABC,∠ACB平分线的交点处
8.
如图4,在△ABC中,EF垂直平分AB,若△BCD的周长为14,AC=8,则BC的长为
(
)
A.
6
B.
8
C.
12
D.
24
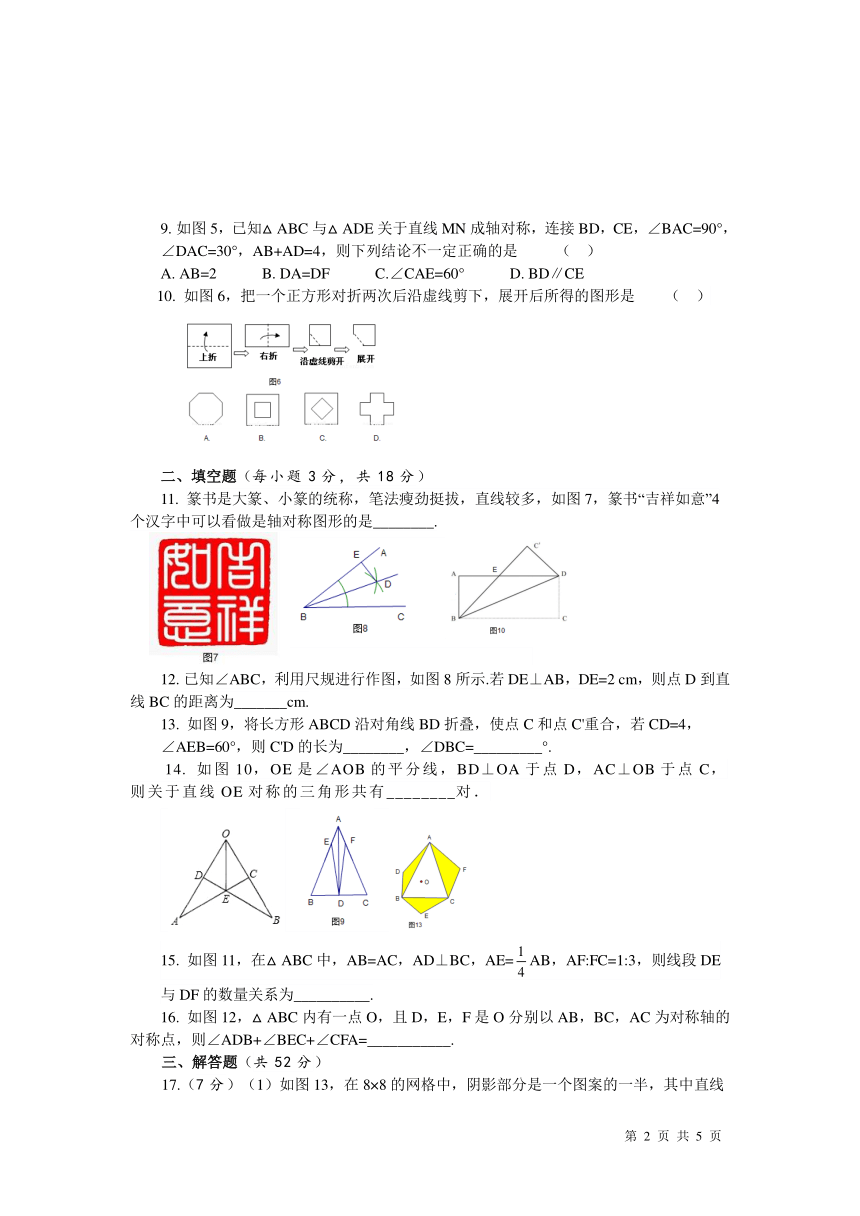
如图5,已知△ABC与△ADE关于直线MN成轴对称,连接BD,CE,∠BAC=90°,∠DAC=30°,AB+AD=4,则下列结论不一定正确的是
(
)
AB=2
B.
DA=DF
C.∠CAE=60°
D.
BD∥CE
10.
如图6,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是
(
)
二、填空题(每小题3分,共18分)
11.
篆书是大篆、小篆的统称,笔法瘦劲挺拔,直线较多,如图7,篆书“吉祥如意”4个汉字中可以看做是轴对称图形的是________.
已知∠ABC,利用尺规进行作图,如图8所示.若DE⊥AB,DE=2
cm,则点D到直线BC的距离为_______cm.
13.
如图9,将长方形ABCD沿对角线BD折叠,使点C和点C'重合,若CD=4,∠AEB=60°,则C'D的长为________,∠DBC=_________°.
14.
如图10,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,则关于直线OE对称的三角形共有________对.
15.
如图11,在△ABC中,AB=AC,AD⊥BC,AE=AB,AF:FC=1:3,则线段DE与DF的数量关系为__________.
16.
如图12,△ABC内有一点O,且D,E,F是O分别以AB,BC,AC为对称轴的对称点,则∠ADB+∠BEC+∠CFA=___________.
三、解答题(共52分)
17.(7分)(1)如图13,在8×8的网格中,阴影部分是一个图案的一半,其中直线AB是这个图案的对称轴,画出这个图案的另一半;
(2)以直线CD为对称轴,画出与(1)的图案成轴对称的图形.
18.(7分)分别画出如图14所示图形(阴影部分)的所有对称轴.
19.(8分)如图15,已知△ABC与△DEF关于直线MN成轴对称,利用尺规作图,分别画出直线MN和△DEF(保留作图痕迹,不写作法).
20.(8分)如图16,在△ABC中,AB=AC,BD=CD,点M是DA延长线上一个动点,连接MB、MC,试判断线段MB与MC的数量关系,并说明理由.
21.(10分)如图17,下列每个5×5的小正方形网格图中有4个小正方形已涂上阴影,请选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形.
22.(12分)如图18,在△ABC中,AB=AC,BD=BC,DE垂直平分AB,AD=m,CD=n,DE=a.
(1)求△ABC的周长(用含m,n的代数式表示);
(2)求△BCD的面积(用含字母的代数式表示).
附加题(共20分,不计入总分)
(8分)如图1,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
2.(12分)如图2,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.试说明:∠ABD=∠BDF.
第五章
生活中的轴对称综合测评
参考答案
一、1.
A
2.
B
3.
B
4.
C
5.
D
6.
C
7.
D
8.
A
9.
B
10.
C
二、11.
吉
12.
2
13.
4
30
14.
4
15.
DE=DF
16.
360°
三、17.解:(1)(2)如图1所示.
图1
图2
图3
解:如图2所示.
19.
解:如图3所示.
20.
解:MB=MC.理由如下:
因为AB=AC,BD=CD,所以AD⊥BC,所以∠MDB=∠MDC=90°.
在△MDB和△MDC中,因为BD=CD,∠MDB=∠MDC,MD=MD,所以△MDB≌△MDC,所以MB=MC.
21.
解:不唯一,如图4所示.
图4
解:(1)因为DE垂直平分AB,所以AD=BD.
因为BD=BC,AD=m,所以BC=AD=m.
因为AD=m,CD=n,所以
AC=AD+CD=m+n,所以AB=AC=m+n.
所以△ABC的周长为AB+AC+BC=m+n+m+n+m=3m+2n.
(2)因为BD=BC,所以∠C=∠BDC,所以∠DBC=180°-2∠C.
因为AB=AC,所以∠A=180°-2∠C,所以∠DBC=∠A.
因为AD=BD,所以∠ABD=∠A,所以∠ABD=∠DBC.
因为DE⊥AB,DE=a,所以点D到BC的距离为a,所以△BCD的面积为am.
附加题
解:如图所示,直线OO′即为所求.
2.
解:因为EF垂直平分BD,所以FB=FD,所以∠DBF=∠BDF.
因为BD是∠ABC的平分线,所以∠ABD=∠DBF,所以∠ABD=∠BDF.
第
6
页
共
8
页
生活中的轴对称综合测评
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1.下列国旗中不是轴对称图形的是
(
)
下列两个图形不是关于某条直线成轴对称的是
(
)
我国传统建筑中,窗框的图案玲珑剔透、千变万化.如图1所示的窗框是一个轴对称图形,其对称轴有
(
)
1条
B.
2条
C.
3条
D.
4条
若等腰三角形的一个内角是80°,则它的底角为
(
)
50°
B.
80°
C.
50°或80°
D.
无法确定
下列判断正确的是
(
)
A.
直角是轴对称图形,对称轴是角平分线
B.
经过线段中点的直线是线段的对称轴
C.
等腰三角形的对称轴是底边上的高
D.
成轴对称的两个三角形一定全等
6.
如图2,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于EF的长为半径作弧,两弧分别交于G,H两点,作直线GH,交EF于点O,连接AO.下列结论正确的是
(
)
A.AO平分∠EAF
B.AO垂直平分EF
C.
GH垂直平分EF
D.GH平分AF
7.
如图3,三条笔直公路两两相交,某石化公司准备在△ABC内修建一个加油站,要求加油站到三条公路的距离相等,则加油站应建在
(
)
AB,AC两边垂直平分线的交点处
B.
AB,AC两边中线的交点处
AB,AC两边高线的交点处
D.∠ABC,∠ACB平分线的交点处
8.
如图4,在△ABC中,EF垂直平分AB,若△BCD的周长为14,AC=8,则BC的长为
(
)
A.
6
B.
8
C.
12
D.
24
如图5,已知△ABC与△ADE关于直线MN成轴对称,连接BD,CE,∠BAC=90°,∠DAC=30°,AB+AD=4,则下列结论不一定正确的是
(
)
AB=2
B.
DA=DF
C.∠CAE=60°
D.
BD∥CE
10.
如图6,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是
(
)
二、填空题(每小题3分,共18分)
11.
篆书是大篆、小篆的统称,笔法瘦劲挺拔,直线较多,如图7,篆书“吉祥如意”4个汉字中可以看做是轴对称图形的是________.
已知∠ABC,利用尺规进行作图,如图8所示.若DE⊥AB,DE=2
cm,则点D到直线BC的距离为_______cm.
13.
如图9,将长方形ABCD沿对角线BD折叠,使点C和点C'重合,若CD=4,∠AEB=60°,则C'D的长为________,∠DBC=_________°.
14.
如图10,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,则关于直线OE对称的三角形共有________对.
15.
如图11,在△ABC中,AB=AC,AD⊥BC,AE=AB,AF:FC=1:3,则线段DE与DF的数量关系为__________.
16.
如图12,△ABC内有一点O,且D,E,F是O分别以AB,BC,AC为对称轴的对称点,则∠ADB+∠BEC+∠CFA=___________.
三、解答题(共52分)
17.(7分)(1)如图13,在8×8的网格中,阴影部分是一个图案的一半,其中直线AB是这个图案的对称轴,画出这个图案的另一半;
(2)以直线CD为对称轴,画出与(1)的图案成轴对称的图形.
18.(7分)分别画出如图14所示图形(阴影部分)的所有对称轴.
19.(8分)如图15,已知△ABC与△DEF关于直线MN成轴对称,利用尺规作图,分别画出直线MN和△DEF(保留作图痕迹,不写作法).
20.(8分)如图16,在△ABC中,AB=AC,BD=CD,点M是DA延长线上一个动点,连接MB、MC,试判断线段MB与MC的数量关系,并说明理由.
21.(10分)如图17,下列每个5×5的小正方形网格图中有4个小正方形已涂上阴影,请选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形.
22.(12分)如图18,在△ABC中,AB=AC,BD=BC,DE垂直平分AB,AD=m,CD=n,DE=a.
(1)求△ABC的周长(用含m,n的代数式表示);
(2)求△BCD的面积(用含字母的代数式表示).
附加题(共20分,不计入总分)
(8分)如图1,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
2.(12分)如图2,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.试说明:∠ABD=∠BDF.
第五章
生活中的轴对称综合测评
参考答案
一、1.
A
2.
B
3.
B
4.
C
5.
D
6.
C
7.
D
8.
A
9.
B
10.
C
二、11.
吉
12.
2
13.
4
30
14.
4
15.
DE=DF
16.
360°
三、17.解:(1)(2)如图1所示.
图1
图2
图3
解:如图2所示.
19.
解:如图3所示.
20.
解:MB=MC.理由如下:
因为AB=AC,BD=CD,所以AD⊥BC,所以∠MDB=∠MDC=90°.
在△MDB和△MDC中,因为BD=CD,∠MDB=∠MDC,MD=MD,所以△MDB≌△MDC,所以MB=MC.
21.
解:不唯一,如图4所示.
图4
解:(1)因为DE垂直平分AB,所以AD=BD.
因为BD=BC,AD=m,所以BC=AD=m.
因为AD=m,CD=n,所以
AC=AD+CD=m+n,所以AB=AC=m+n.
所以△ABC的周长为AB+AC+BC=m+n+m+n+m=3m+2n.
(2)因为BD=BC,所以∠C=∠BDC,所以∠DBC=180°-2∠C.
因为AB=AC,所以∠A=180°-2∠C,所以∠DBC=∠A.
因为AD=BD,所以∠ABD=∠A,所以∠ABD=∠DBC.
因为DE⊥AB,DE=a,所以点D到BC的距离为a,所以△BCD的面积为am.
附加题
解:如图所示,直线OO′即为所求.
2.
解:因为EF垂直平分BD,所以FB=FD,所以∠DBF=∠BDF.
因为BD是∠ABC的平分线,所以∠ABD=∠DBF,所以∠ABD=∠BDF.
第
6
页
共
8
页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
