高一数学(人教B版)-平面与平面垂直的概念-课件(55张PPT)
文档属性
| 名称 | 高一数学(人教B版)-平面与平面垂直的概念-课件(55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览











文档简介
(共55张PPT)
高一年级
数学
平面与平面垂直的概念
知识回顾
线面平行
面面平行
线线平行
知识回顾
m
n
β
β
空间中的平行
m
n
m
m’
α
O
线面平行
面面平行
线线平行
知识回顾
β
α
β
α
空间中的平行
m
n
m
n
m
n
知识回顾
直线与平面垂直
定义
直线垂直于平面内与其具有公共点的所有直线
知识回顾
直线与平面垂直
判定定理
充要条件
直线与平面内两条相交直线垂直,则直线与平面垂直.
直线垂直于平面内的任意直线.
知识回顾
直线与平面垂直
性质定理
判定定理
充要条件
直线与平面内两条相交直线垂直,则直线与平面垂直.
直线垂直于平面内的任意直线.
如果两条直线垂直于同一个平面,则这两条直线平行.
两条平行直线中的一条垂直于一个平面,则另一条直
线也垂直于这个平面.
笔记本电脑在打开的过程中,会给人以面面“夹角”变大的感觉.你认为应该怎样刻画面面“夹角”呢?
新课引入
新课引入
O
a
b
O
a
b
a
b
平面中的角:从一点出发的两条射线构成角.记作?AOB.
A
B
O
讲授新课
射线
射线
直线上的一点将直线分成两部分,每一部分都叫做射线.
A
B
O
平面内的一条直线将平面分成两部分,每一部分叫半平面.
半平面
半平面
讲授新课
直线上的一
点
将直线分成两部分,每一部分都叫做射线.
射线
射线
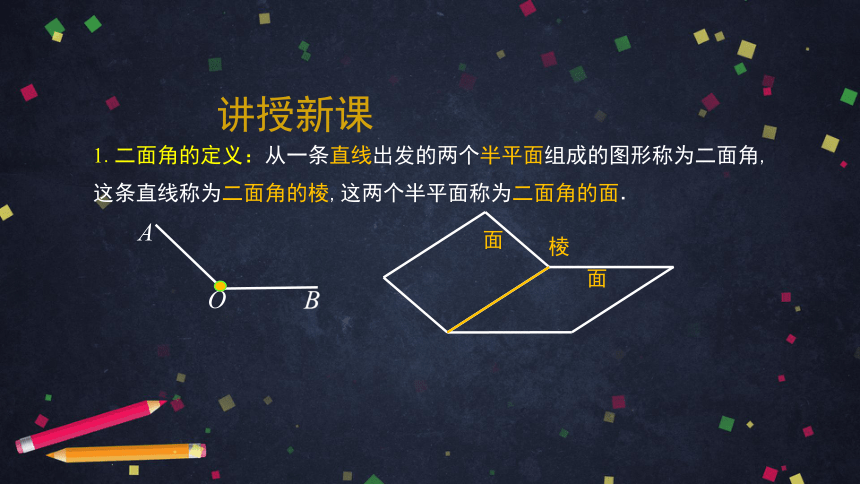
1.二面角的定义:从一条直线出发的两个半平面组成的图形称为二面角,
这条直线称为二面角的棱,这两个半平面称为二面角的面.
讲授新课
棱
面
面
B
O
A
讲授新课
2.二面角的表示:
?
?
?
?
讲授新课
3.二面角的画法:“见者实、遮者虚”
l
l
讲授新课
4.二面角的大小:在二面角?-l-?
的棱
l
上任取一点O,在半平面
?
和?
内,从点
O
分别作垂直于棱
l
的射线OA、OB,射线OA、OB组成的∠AOB叫做二面角
?-l-?
的平面角.
O
A
B
l
α
β
O
讲授新课
4.二面角的大小:在二面角?-l-?
的棱
l
上任取一点O,在半平面
?
和?
内,从点
O
分别作垂直于棱
l
的射线OA、OB,射线OA、OB组成的∠AOB叫做二面角
?-l-?
的平面角.特别地,平面角是直角的二面角称为直二面角.
O
A
B
l
α
β
讲授新课
注意1:二面角
?-l-?
的平面角∠AOB的大小与点O在棱l上位置无关.
O
A
B
l
α
β
C
E
F
讲授新课
5.二面角?-l-?的范围:
l
α
β
l
α
β
l
α
β
[0,π]
A
O
B
讲授新课
注意2:两个平面相交时所成角的大小,指的是它们所形成的四个二面角中,不大于直角的角的大小.
l
α
β
l
α
β
l
α
β
讲授新课
O
A
B
O
A
B
O
A
B
讲授新课
6、两个平面垂直的定义:如果两个平面?,?相交所成的二面角是直二面角,则称此时这两个平面互相垂直.记作:???.
α
β
l
O
A
B
讲授新课
α
β
6、两个平面垂直的定义:如果两个平面?,?相交所成的二面角是直角,即直二面角,则称此时这两个平面互相垂直.记作:???.
l
l
α
β
讲授新课
思考1:已知,二面角α-l-β是锐角,过二面角α-l-β的半平面α内一点A(A
不在棱l上),作另一个半平面β的垂线,垂足为B.过点B作棱l的垂线,垂足为O,连结AO,则∠AOB是二面角α-l-β的平面角吗?为什么?
l
α
β
B
略解:因为AB?β,所以AB?
l.
因为OB?
l,
所以,l?平面AOB.
所以,l?AO.
∠AOB是二面角α-l-β的平面角.
A
O
讲授新课
l
α
β
B
A
O
思考1:如图,过锐二面角α-l-β的半平面α内一点A(A不在棱l上),作另一个半平面β的垂线,垂足为B.过点B作棱l的垂线,垂足为O,连结AO,则∠AOB是二面角α-l-β的平面角.
讲授新课
思考2:如图,平面γ
垂直于二面角α-l-β
的棱l,
分别与面α、β相交于OA、OB,则∠AOB是二
面角α-l-β的平面角吗?为什么?
β
l
A
O
B
γ
α
略解:因为l?面γ,
所以,l
?AO,且
l
?BO.
∠AOB是二面角α-l-β的平面角.
讲授新课
思考2:如图,平面γ
垂直于二面角α-l-β
的棱l,
分别与面α、β相交于OA、OB,则∠AOB是二
面角α-l-β的平面角.
β
l
A
O
B
γ
α
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
B
A
O
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
2.作垂面:作与棱垂直的平面与
两半平面的交线得到二面角的平
面角.
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
2.作垂面:作与棱垂直的平面与
两半平面的交线得到二面角的平
面角.
3.作垂线:做出半平面的垂线,利用线面垂直的知识作出二面角的平面角.
二面角的平面角的作法总结:
1.定义法:依据定义
2.作垂面:作与棱垂直的平面,利用与两半平面的交线
3.作垂线:做出半平面的垂线,利用线面垂直的知识
典型例题
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为________.
典型例题
β1
α1
l1
β2
α2
l2
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为________.
图一
典型例题
β1
α1
l1
β2
α2
l2
相等或者互补
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
图二
典型例题
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
无关
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
无关
门
墙
墙
地
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
平面几何中的命题:“在平面内,如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补”.
平面几何中的命题:“在平面内,如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补”.
例.在正方体ABCD-A1B1C1D1中,
(1)求二面角D-AB-D1的大小,
(2)求二面角B1-AC-B的正切值,
(3)求证:平面ABC1D1┴平面A1B1CD.
典型例题
A
A1
B
C
D
B1
C1
D1
典型例题
A
A1
B
C
D
B1
C1
D1
例.在正方体ABCD-A1B1C1D1中,
(1)求二面角D-AB-D1的大小,
典型例题
A
A1
B
C
D
B1
C1
D1
解答:
证
指
算
作
典型例题
A
A1
B
C
D
B1
C1
D1
例.在正方体ABCD-A1B1C1D1中,
(2)求二面角B1-AC-B的正切值,
典型例题
A
A1
B
C
D
B1
C1
D1
O
解答:
证
指
算
作
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
(3)求证:平面ABC1D1┴平面A1B1CD.
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
(3)求证:平面ABC1D1┴平面A1B1CD.
(3)求证:平面FEC1D1┴平面A1B1EF.
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
证
指
作
解答:
算
求解二面角的过程总结:求二面角的大小,一般先利用二面角的定义、作二面角棱的垂面、作面的垂线等等方法做出二面角的平面角,并证明所作角为二面角的平面角,通过解平面角所在的三角形求得平面角.其解题过程也称为“作、证、指、算”.
课堂练习
三棱锥A-BCD中,AB=BC=CD=DA=AC=a,
BD=
a,
求:
二面角A-BD-C的大小.
B
C
D
A
解答 取BD的中点为O,分别连AO、CO
因为AB=AD=a,所以AO⊥BD,
同理,CO⊥BD
所以∠AOC为二面角A-BD-C的平面角.
因为AB=AD=a,BD=
a,
在ΔAOC中,
,
OA2+OC2=AC2
所以∠AOC=90°
即二面角A-BD-C的大小为90°.
B
C
D
A
O
证
指
作
算
AC=a
1.二面角
课堂小结
2.平面与平面垂直的定义
定义
范围
作法
步骤
棱上取点、分别在两个半平面内、与棱垂直射线
[0,π]
定义、棱的垂面、面的垂线
作、证、指、算
直二面角
1、判断下列命题的真假:
(1)过平面外一点只可作一个平面与已知平面垂直.
(2)已知平面
满足
,
则
.
课后作业
2、已知正四面体A-BCD,
求:二面角A—DC—B的余弦值.
高一年级
数学
立体几何
高一年级
数学
平面与平面垂直的概念
知识回顾
线面平行
面面平行
线线平行
知识回顾
m
n
β
β
空间中的平行
m
n
m
m’
α
O
线面平行
面面平行
线线平行
知识回顾
β
α
β
α
空间中的平行
m
n
m
n
m
n
知识回顾
直线与平面垂直
定义
直线垂直于平面内与其具有公共点的所有直线
知识回顾
直线与平面垂直
判定定理
充要条件
直线与平面内两条相交直线垂直,则直线与平面垂直.
直线垂直于平面内的任意直线.
知识回顾
直线与平面垂直
性质定理
判定定理
充要条件
直线与平面内两条相交直线垂直,则直线与平面垂直.
直线垂直于平面内的任意直线.
如果两条直线垂直于同一个平面,则这两条直线平行.
两条平行直线中的一条垂直于一个平面,则另一条直
线也垂直于这个平面.
笔记本电脑在打开的过程中,会给人以面面“夹角”变大的感觉.你认为应该怎样刻画面面“夹角”呢?
新课引入
新课引入
O
a
b
O
a
b
a
b
平面中的角:从一点出发的两条射线构成角.记作?AOB.
A
B
O
讲授新课
射线
射线
直线上的一点将直线分成两部分,每一部分都叫做射线.
A
B
O
平面内的一条直线将平面分成两部分,每一部分叫半平面.
半平面
半平面
讲授新课
直线上的一
点
将直线分成两部分,每一部分都叫做射线.
射线
射线
1.二面角的定义:从一条直线出发的两个半平面组成的图形称为二面角,
这条直线称为二面角的棱,这两个半平面称为二面角的面.
讲授新课
棱
面
面
B
O
A
讲授新课
2.二面角的表示:
?
?
?
?
讲授新课
3.二面角的画法:“见者实、遮者虚”
l
l
讲授新课
4.二面角的大小:在二面角?-l-?
的棱
l
上任取一点O,在半平面
?
和?
内,从点
O
分别作垂直于棱
l
的射线OA、OB,射线OA、OB组成的∠AOB叫做二面角
?-l-?
的平面角.
O
A
B
l
α
β
O
讲授新课
4.二面角的大小:在二面角?-l-?
的棱
l
上任取一点O,在半平面
?
和?
内,从点
O
分别作垂直于棱
l
的射线OA、OB,射线OA、OB组成的∠AOB叫做二面角
?-l-?
的平面角.特别地,平面角是直角的二面角称为直二面角.
O
A
B
l
α
β
讲授新课
注意1:二面角
?-l-?
的平面角∠AOB的大小与点O在棱l上位置无关.
O
A
B
l
α
β
C
E
F
讲授新课
5.二面角?-l-?的范围:
l
α
β
l
α
β
l
α
β
[0,π]
A
O
B
讲授新课
注意2:两个平面相交时所成角的大小,指的是它们所形成的四个二面角中,不大于直角的角的大小.
l
α
β
l
α
β
l
α
β
讲授新课
O
A
B
O
A
B
O
A
B
讲授新课
6、两个平面垂直的定义:如果两个平面?,?相交所成的二面角是直二面角,则称此时这两个平面互相垂直.记作:???.
α
β
l
O
A
B
讲授新课
α
β
6、两个平面垂直的定义:如果两个平面?,?相交所成的二面角是直角,即直二面角,则称此时这两个平面互相垂直.记作:???.
l
l
α
β
讲授新课
思考1:已知,二面角α-l-β是锐角,过二面角α-l-β的半平面α内一点A(A
不在棱l上),作另一个半平面β的垂线,垂足为B.过点B作棱l的垂线,垂足为O,连结AO,则∠AOB是二面角α-l-β的平面角吗?为什么?
l
α
β
B
略解:因为AB?β,所以AB?
l.
因为OB?
l,
所以,l?平面AOB.
所以,l?AO.
∠AOB是二面角α-l-β的平面角.
A
O
讲授新课
l
α
β
B
A
O
思考1:如图,过锐二面角α-l-β的半平面α内一点A(A不在棱l上),作另一个半平面β的垂线,垂足为B.过点B作棱l的垂线,垂足为O,连结AO,则∠AOB是二面角α-l-β的平面角.
讲授新课
思考2:如图,平面γ
垂直于二面角α-l-β
的棱l,
分别与面α、β相交于OA、OB,则∠AOB是二
面角α-l-β的平面角吗?为什么?
β
l
A
O
B
γ
α
略解:因为l?面γ,
所以,l
?AO,且
l
?BO.
∠AOB是二面角α-l-β的平面角.
讲授新课
思考2:如图,平面γ
垂直于二面角α-l-β
的棱l,
分别与面α、β相交于OA、OB,则∠AOB是二
面角α-l-β的平面角.
β
l
A
O
B
γ
α
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
B
A
O
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
2.作垂面:作与棱垂直的平面与
两半平面的交线得到二面角的平
面角.
二面角的平面角的作法总结:
1.定义法:依据定义作出二面角
的平面角
2.作垂面:作与棱垂直的平面与
两半平面的交线得到二面角的平
面角.
3.作垂线:做出半平面的垂线,利用线面垂直的知识作出二面角的平面角.
二面角的平面角的作法总结:
1.定义法:依据定义
2.作垂面:作与棱垂直的平面,利用与两半平面的交线
3.作垂线:做出半平面的垂线,利用线面垂直的知识
典型例题
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为________.
典型例题
β1
α1
l1
β2
α2
l2
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为________.
图一
典型例题
β1
α1
l1
β2
α2
l2
相等或者互补
例.如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
图二
典型例题
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
无关
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
β1
α1
l1
α2
β2
l2
无关
门
墙
墙
地
例.如果一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角的大小关系为_____________.
典型例题
平面几何中的命题:“在平面内,如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补”.
平面几何中的命题:“在平面内,如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补”.
例.在正方体ABCD-A1B1C1D1中,
(1)求二面角D-AB-D1的大小,
(2)求二面角B1-AC-B的正切值,
(3)求证:平面ABC1D1┴平面A1B1CD.
典型例题
A
A1
B
C
D
B1
C1
D1
典型例题
A
A1
B
C
D
B1
C1
D1
例.在正方体ABCD-A1B1C1D1中,
(1)求二面角D-AB-D1的大小,
典型例题
A
A1
B
C
D
B1
C1
D1
解答:
证
指
算
作
典型例题
A
A1
B
C
D
B1
C1
D1
例.在正方体ABCD-A1B1C1D1中,
(2)求二面角B1-AC-B的正切值,
典型例题
A
A1
B
C
D
B1
C1
D1
O
解答:
证
指
算
作
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
(3)求证:平面ABC1D1┴平面A1B1CD.
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
(3)求证:平面ABC1D1┴平面A1B1CD.
(3)求证:平面FEC1D1┴平面A1B1EF.
典型例题
A
A1
B
C
D
B1
C1
D1
E
F
证
指
作
解答:
算
求解二面角的过程总结:求二面角的大小,一般先利用二面角的定义、作二面角棱的垂面、作面的垂线等等方法做出二面角的平面角,并证明所作角为二面角的平面角,通过解平面角所在的三角形求得平面角.其解题过程也称为“作、证、指、算”.
课堂练习
三棱锥A-BCD中,AB=BC=CD=DA=AC=a,
BD=
a,
求:
二面角A-BD-C的大小.
B
C
D
A
解答 取BD的中点为O,分别连AO、CO
因为AB=AD=a,所以AO⊥BD,
同理,CO⊥BD
所以∠AOC为二面角A-BD-C的平面角.
因为AB=AD=a,BD=
a,
在ΔAOC中,
,
OA2+OC2=AC2
所以∠AOC=90°
即二面角A-BD-C的大小为90°.
B
C
D
A
O
证
指
作
算
AC=a
1.二面角
课堂小结
2.平面与平面垂直的定义
定义
范围
作法
步骤
棱上取点、分别在两个半平面内、与棱垂直射线
[0,π]
定义、棱的垂面、面的垂线
作、证、指、算
直二面角
1、判断下列命题的真假:
(1)过平面外一点只可作一个平面与已知平面垂直.
(2)已知平面
满足
,
则
.
课后作业
2、已知正四面体A-BCD,
求:二面角A—DC—B的余弦值.
高一年级
数学
立体几何
