高一数学(人教B版)-平面与平面垂直的判定与性质-课件(43张PPT)
文档属性
| 名称 | 高一数学(人教B版)-平面与平面垂直的判定与性质-课件(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览









文档简介
(共43张PPT)
高一年级
数学
平面与平面垂直的判定与性质
知识回顾
二面角
作法
范围
定义
[0,π]
从一条直线出发的两个半平面组成的图形称为二面角
作(定义、棱的垂面、面的垂线)、证、指、算
平面与平面垂直的概念
直二面角
知识回顾
思考1.在二面角α-m-β中,
如果AO⊥β于点O,那么二面角α-m-β
是直二面角吗?
新课引入
α
β
m
A
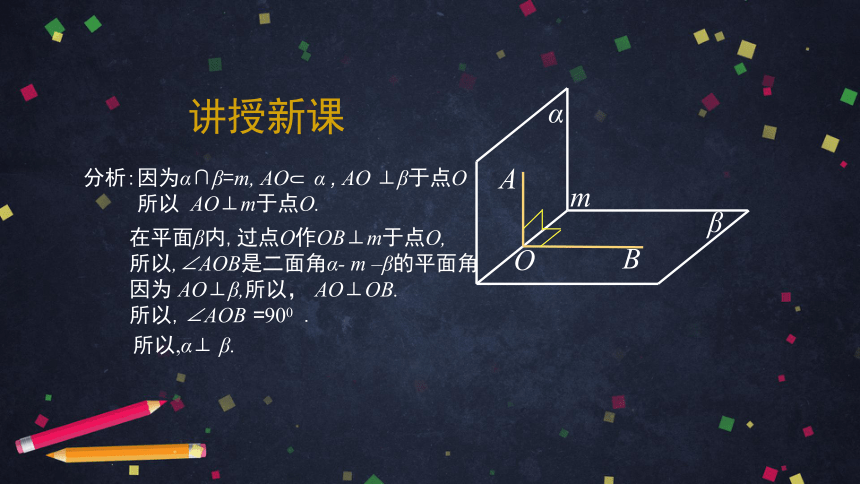
讲授新课
O
α
β
m
A
分析:因为α∩β=m,
AO?
α
,
AO
⊥β于点O
所以
AO⊥m于点O.
在平面β内,过点O作OB⊥m于点O,
所以,∠AOB是二面角α-
m
–β的平面角
因为
AO⊥β,所以,
AO⊥OB.
所以,∠AOB
=900
.
O
B
所以,α⊥
β.
讲授新课
平面与平面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
讲授新课
α
β
m
l
线面垂直
面面垂直
平面与平面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
讲授新课
思考2:如果平面α⊥平面β,那么平面α内的任一条直线都与平面β垂直吗?
α
β
a
b
m
讲授新课
思考2:如果平面α⊥平面β,那么平面α内的任一条直线都与平面β垂直吗?
α
β
m
讲授新课
c
α
β
m
O
A
讲授新课
(
?)
α
β
m
B
证明:AO
m
于点O,
过点O在平面β内作OB⊥m,
则∠AOB是二面角α-m-
β
的平面角.
因为α
β,所以∠AOB
=900.因此,AO
OB.
又因为AO
m,
m∩OB
O.m?
β
,且OB?
β.
所以,
AO
β
.
O
A
讲授新课
线线垂直
线面垂直
面面垂直
α
β
m
A
O
平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
讲授新课
符号语言
图形语言
面面垂直的判定定理:
讲授新课
线面垂直
面面垂直
线线垂直
线面垂直
面面垂直
面面垂直的性质定理:
空间中的垂直关系
m
n
l
m
n
l
α
l
α
线面垂直
面面垂直
线线垂直
判定
判定
m
n
l
m
n
l
α
l
α
β
空间中的垂直关系
线面垂直
面面垂直
线线垂直
性质
定义
n
l
n
l
α
l
α
β
判定
判定
空间中的垂直关系
例.判断以下命题是否正确:
例题讲解
(1).如果平面α内有一条直线垂直于平面β内的一条直线,则α⊥β.(
)
×
A
A1
B
C
D
B1
C1
D1
(2).如果平面α内有一条直线垂直于平面β内的两条直线,则α⊥β.(
)
×
A
A1
B
C
D
B1
C1
D1
(3).
如果平面α内的一条直线
l
垂直于平面β内的两条相交直线,
则α⊥β.(
)
√
l⊥β
,l
?
α,则α⊥β.
(4).如果α⊥β,那么平面α内的所有直线都垂直于平面β.(
)
A
A1
B
C
D
B1
C1
D1
×
(5).若两个平面垂直,分别在这两个平面内直线互相垂直.(
)
A
A1
B
C
D
B1
C1
D1
×
(6).若两个平面垂直,分别在两个平面内且互相垂直的两条直线一定分别与另一个平面垂直.(
)
A
A1
B
C
D
B1
C1
D1
×
(7).若两个平面互相垂直,过一个平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面.(
)
√
例.在正方体ABCD-A1B1C1D1中,
求证:平面ABC1D1┴平面A1B1CD.
A
A1
B
C
D
B1
C1
D1
A
A1
B
C
D
B1
C1
D1
证明:因为正方体ABCD-A1B1C1D1,
所以,
AB┴平面A1D1DA,
AB┴
A1D.
在正方形A1D1DA中,AD1
┴A1D,
AB
∩
AD1
=A,
所以,A1D┴平面ABC1D1.
又因为A1D?平面A1B1CD,
所以,平面A1B1CD┴平面
ABC1D1.
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
求证:平面ABC1D1┴平面A1B1CD.
思路二:
例.已知,如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
求证:平面PAC⊥平面PBC.
A
B
O
C
P
证明:设⊙O所在平面为α,因为PA⊥α,BC?α,
所以,PA⊥BC.
因为AB为⊙O的直径,点C在⊙O上,所以,∠BCA=
90°,
即BC⊥AC.
因为PA∩AC=A,
所以,BC⊥平面PAC.
因为,BC?面PBC.
所以,平面PBC⊥平面PAC.
线面垂直
面面垂直
线线垂直
A
B
O
C
P
判断面面垂直的方法:利用直二面角、面面垂直的判定定理.
小结
α
β
m
O
A
α
β
m
O
A
n
B
l
判断面面垂直的方法:利用直二面角、面面垂直的判定定理.
小结
线线垂直
面面垂直
线面垂直
直角三角形的定义
勾股逆定理
直径所对圆周角是直角
线面垂直的定义
线面垂直的性质
A
B
C
D
例.已知,在三棱锥
A-BCD中,
AB⊥平面BCD,BC⊥CD.请问在三棱锥
A-BCD中,哪些平面相互垂直,为什么?
AB⊥平面BCD
平面ABC⊥平面BCD
AB⊥平面BCD
平面ABD⊥平面BCD
CD⊥平面ABC
平面ACD⊥平面ABC
BC⊥CD
AB⊥平面BCD
AB⊥CD
小结
寻找已知平面的垂面的关键:寻找已知平面的垂线.
A
B
C
D
例.已知,在三棱锥
A-BCD中,
AB⊥平面BCD,BC⊥CD.请问在三棱锥
A-BCD中,哪些平面相互垂直,为什么?
平面ABC⊥平面BCD
平面ABD⊥平面BCD
AB⊥平面BCD
?
α
β
l
γ
m
n
拓展:已知:
α
∩
β=
l,
α
⊥γ
,
α
∩
γ
=m,
β⊥γ,
β
∩
γ
=n
.
求证:l
⊥
γ
.
α
β
l
γ
m
n
O
A
B
解法一:在面γ
内作取点O,点O
不在n、m
上,作OA⊥m于点
A,
OB⊥n于点
B,
因为
α⊥γ,α
∩
γ
=
m,OA⊥m,AO?γ,
所以,
OA⊥α,
l
?α
,
OA⊥l.
同理,
OB⊥l.
OB
∩OA=O,OB
?
γ
,OA?
γ
所以:l
⊥
γ
.
线面垂直定义
面面垂直性质定理
线面垂直判定定理
α
β
l
γ
m
n
垂直于同一个平面α的两个平面若相交,则其交线垂直于平面α.
已知:如图所示,
α
⊥
β
,在
α
与
β
的交线上取线段
,且AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=1,BD=2,求CD的长.
α
β
A
l
C
D
B
α
β
A
l
C
D
B
解:连接BC,
因为
α
⊥
β,α
∩
β
=AB,BD?
β
,
BD
⊥AB,
所以,DB
⊥
α
.
又因为
BC?
α
,
所以,BD
⊥BC,
因此,
是直角三角形.
在
中,
在
中,
.
已知:如图所示,
α
⊥
β
,在
α
与
β
的交线上取线段
,且AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=1,BD=2,求CD的长.
α
β
A
l
C
D
B
课堂小结
1、面面垂直的判定定理:证明两个平面相互垂直、寻找平面的垂面
2、判断两个平面互相垂直的方法:⑴定义
⑵判定定理
3、面面垂直的性质定理:线面垂直的判断方法
1.过平面α的一条垂线可作_____个平面与平面α垂直.
2.过一点可作____个平面与已知平面垂直.
一、填空题:
3.过平面α的一条斜线,可作____个平面与平面α垂直.
课后作业
二、在正方体ABCD-A1B1C1D1中,
求证:平面ACD1⊥平面BDD1B1.
高一年级
数学
平面与平面垂直的判定与性质
知识回顾
二面角
作法
范围
定义
[0,π]
从一条直线出发的两个半平面组成的图形称为二面角
作(定义、棱的垂面、面的垂线)、证、指、算
平面与平面垂直的概念
直二面角
知识回顾
思考1.在二面角α-m-β中,
如果AO⊥β于点O,那么二面角α-m-β
是直二面角吗?
新课引入
α
β
m
A
讲授新课
O
α
β
m
A
分析:因为α∩β=m,
AO?
α
,
AO
⊥β于点O
所以
AO⊥m于点O.
在平面β内,过点O作OB⊥m于点O,
所以,∠AOB是二面角α-
m
–β的平面角
因为
AO⊥β,所以,
AO⊥OB.
所以,∠AOB
=900
.
O
B
所以,α⊥
β.
讲授新课
平面与平面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
讲授新课
α
β
m
l
线面垂直
面面垂直
平面与平面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
讲授新课
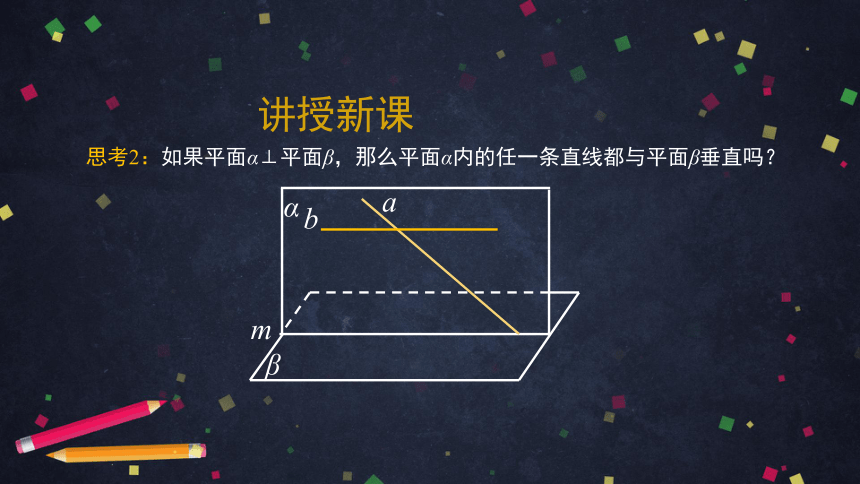
思考2:如果平面α⊥平面β,那么平面α内的任一条直线都与平面β垂直吗?
α
β
a
b
m
讲授新课
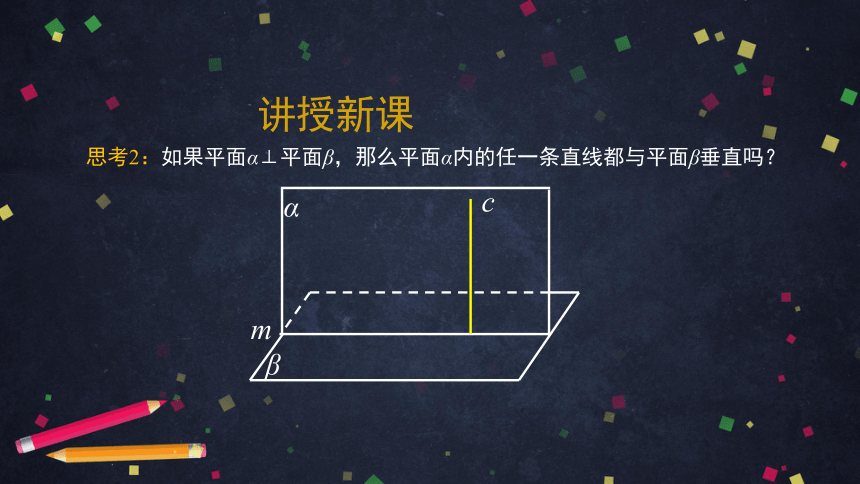
思考2:如果平面α⊥平面β,那么平面α内的任一条直线都与平面β垂直吗?
α
β
m
讲授新课
c
α
β
m
O
A
讲授新课
(
?)
α
β
m
B
证明:AO
m
于点O,
过点O在平面β内作OB⊥m,
则∠AOB是二面角α-m-
β
的平面角.
因为α
β,所以∠AOB
=900.因此,AO
OB.
又因为AO
m,
m∩OB
O.m?
β
,且OB?
β.
所以,
AO
β
.
O
A
讲授新课
线线垂直
线面垂直
面面垂直
α
β
m
A
O
平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
讲授新课
符号语言
图形语言
面面垂直的判定定理:
讲授新课
线面垂直
面面垂直
线线垂直
线面垂直
面面垂直
面面垂直的性质定理:
空间中的垂直关系
m
n
l
m
n
l
α
l
α
线面垂直
面面垂直
线线垂直
判定
判定
m
n
l
m
n
l
α
l
α
β
空间中的垂直关系
线面垂直
面面垂直
线线垂直
性质
定义
n
l
n
l
α
l
α
β
判定
判定
空间中的垂直关系
例.判断以下命题是否正确:
例题讲解
(1).如果平面α内有一条直线垂直于平面β内的一条直线,则α⊥β.(
)
×
A
A1
B
C
D
B1
C1
D1
(2).如果平面α内有一条直线垂直于平面β内的两条直线,则α⊥β.(
)
×
A
A1
B
C
D
B1
C1
D1
(3).
如果平面α内的一条直线
l
垂直于平面β内的两条相交直线,
则α⊥β.(
)
√
l⊥β
,l
?
α,则α⊥β.
(4).如果α⊥β,那么平面α内的所有直线都垂直于平面β.(
)
A
A1
B
C
D
B1
C1
D1
×
(5).若两个平面垂直,分别在这两个平面内直线互相垂直.(
)
A
A1
B
C
D
B1
C1
D1
×
(6).若两个平面垂直,分别在两个平面内且互相垂直的两条直线一定分别与另一个平面垂直.(
)
A
A1
B
C
D
B1
C1
D1
×
(7).若两个平面互相垂直,过一个平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面.(
)
√
例.在正方体ABCD-A1B1C1D1中,
求证:平面ABC1D1┴平面A1B1CD.
A
A1
B
C
D
B1
C1
D1
A
A1
B
C
D
B1
C1
D1
证明:因为正方体ABCD-A1B1C1D1,
所以,
AB┴平面A1D1DA,
AB┴
A1D.
在正方形A1D1DA中,AD1
┴A1D,
AB
∩
AD1
=A,
所以,A1D┴平面ABC1D1.
又因为A1D?平面A1B1CD,
所以,平面A1B1CD┴平面
ABC1D1.
A
A1
B
C
D
B1
C1
D1
E
F
例.在正方体ABCD-A1B1C1D1中,
求证:平面ABC1D1┴平面A1B1CD.
思路二:
例.已知,如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
求证:平面PAC⊥平面PBC.
A
B
O
C
P
证明:设⊙O所在平面为α,因为PA⊥α,BC?α,
所以,PA⊥BC.
因为AB为⊙O的直径,点C在⊙O上,所以,∠BCA=
90°,
即BC⊥AC.
因为PA∩AC=A,
所以,BC⊥平面PAC.
因为,BC?面PBC.
所以,平面PBC⊥平面PAC.
线面垂直
面面垂直
线线垂直
A
B
O
C
P
判断面面垂直的方法:利用直二面角、面面垂直的判定定理.
小结
α
β
m
O
A
α
β
m
O
A
n
B
l
判断面面垂直的方法:利用直二面角、面面垂直的判定定理.
小结
线线垂直
面面垂直
线面垂直
直角三角形的定义
勾股逆定理
直径所对圆周角是直角
线面垂直的定义
线面垂直的性质
A
B
C
D
例.已知,在三棱锥
A-BCD中,
AB⊥平面BCD,BC⊥CD.请问在三棱锥
A-BCD中,哪些平面相互垂直,为什么?
AB⊥平面BCD
平面ABC⊥平面BCD
AB⊥平面BCD
平面ABD⊥平面BCD
CD⊥平面ABC
平面ACD⊥平面ABC
BC⊥CD
AB⊥平面BCD
AB⊥CD
小结
寻找已知平面的垂面的关键:寻找已知平面的垂线.
A
B
C
D
例.已知,在三棱锥
A-BCD中,
AB⊥平面BCD,BC⊥CD.请问在三棱锥
A-BCD中,哪些平面相互垂直,为什么?
平面ABC⊥平面BCD
平面ABD⊥平面BCD
AB⊥平面BCD
?
α
β
l
γ
m
n
拓展:已知:
α
∩
β=
l,
α
⊥γ
,
α
∩
γ
=m,
β⊥γ,
β
∩
γ
=n
.
求证:l
⊥
γ
.
α
β
l
γ
m
n
O
A
B
解法一:在面γ
内作取点O,点O
不在n、m
上,作OA⊥m于点
A,
OB⊥n于点
B,
因为
α⊥γ,α
∩
γ
=
m,OA⊥m,AO?γ,
所以,
OA⊥α,
l
?α
,
OA⊥l.
同理,
OB⊥l.
OB
∩OA=O,OB
?
γ
,OA?
γ
所以:l
⊥
γ
.
线面垂直定义
面面垂直性质定理
线面垂直判定定理
α
β
l
γ
m
n
垂直于同一个平面α的两个平面若相交,则其交线垂直于平面α.
已知:如图所示,
α
⊥
β
,在
α
与
β
的交线上取线段
,且AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=1,BD=2,求CD的长.
α
β
A
l
C
D
B
α
β
A
l
C
D
B
解:连接BC,
因为
α
⊥
β,α
∩
β
=AB,BD?
β
,
BD
⊥AB,
所以,DB
⊥
α
.
又因为
BC?
α
,
所以,BD
⊥BC,
因此,
是直角三角形.
在
中,
在
中,
.
已知:如图所示,
α
⊥
β
,在
α
与
β
的交线上取线段
,且AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=1,BD=2,求CD的长.
α
β
A
l
C
D
B
课堂小结
1、面面垂直的判定定理:证明两个平面相互垂直、寻找平面的垂面
2、判断两个平面互相垂直的方法:⑴定义
⑵判定定理
3、面面垂直的性质定理:线面垂直的判断方法
1.过平面α的一条垂线可作_____个平面与平面α垂直.
2.过一点可作____个平面与已知平面垂直.
一、填空题:
3.过平面α的一条斜线,可作____个平面与平面α垂直.
课后作业
二、在正方体ABCD-A1B1C1D1中,
求证:平面ACD1⊥平面BDD1B1.
