高一数学(人教B版)-空间中的平行和垂直的综合应用(一)-课件(55张PPT)
文档属性
| 名称 | 高一数学(人教B版)-空间中的平行和垂直的综合应用(一)-课件(55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 36.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览









文档简介
(共55张PPT)
高一年级
数学
空间中平行和垂直的综合应用(一)
证明线面平行、线面垂直有哪些方法?
证明面面平行、面面垂直有哪些方法?
【知识回顾】
【知识回顾】
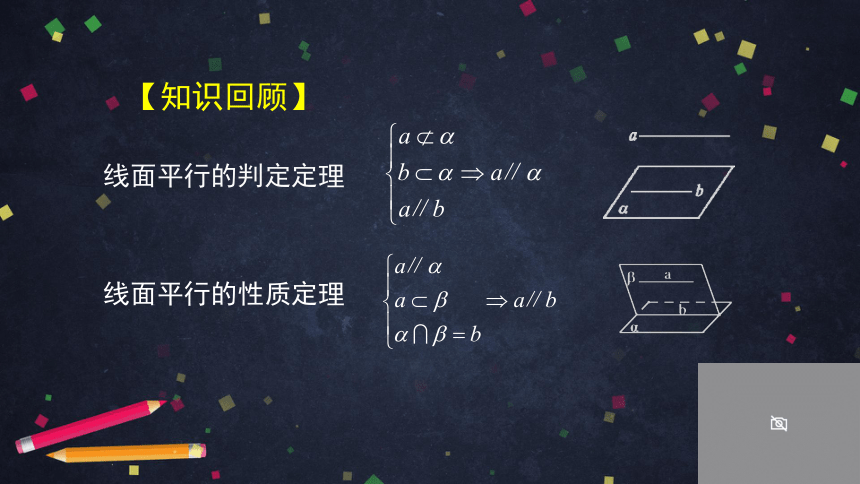
线面平行的判定定理
线面平行的性质定理
【知识回顾】
面面平行的判定定理
面面平行的判定定理推论
c
d
【知识回顾】
面面平行的性质定理
【知识回顾】
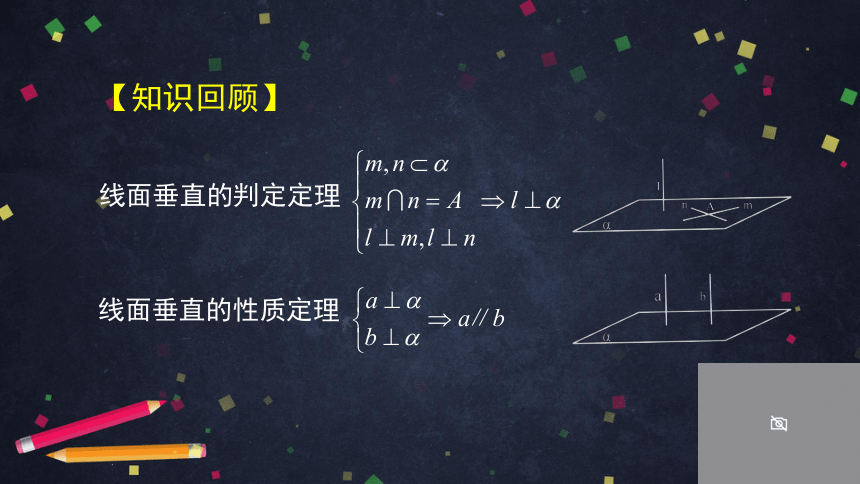
线面垂直的判定定理
线面垂直的性质定理
【知识回顾】
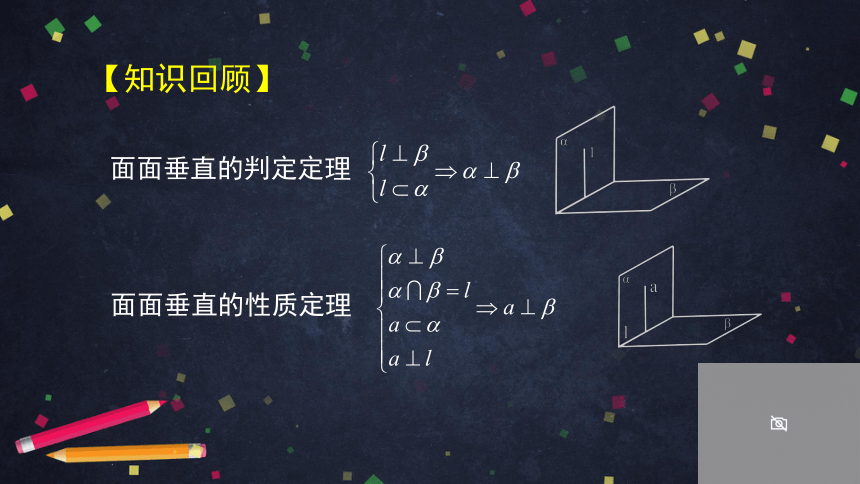
面面垂直的判定定理
面面垂直的性质定理
平行与垂直的相互转化
垂直于同一个平面的两条直线平行,即
与平面的垂线平行的直线也垂直于这个平面,
即
通过前面几节课的学习,我们认识了空间中的点、线、面的位置关系,重点学习了空间中的平行关系和垂直关系,这节课我们将探究空间中平行和垂直的综合应用问题,进一步提升解决立体几何综合问题的能力.
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
【真题面对面】
PA=AD.求证:
(1)AF
平面PEC
(2)
AF
平面PCD
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
PA=AD.求证:
(1)AF
平面PEC
思路一:通过构造平行四边形生成线线平行关系
(1)证法一:取PC的中点G,连接EG,FG
点F是PD的中点,
GF
CD,GF=
CD
点E是AB的中点,
EA=
AB
在平行四边形ABCD中,AB
CD,AB=CD
GF
AE,GF=AE,
四边形AEGF是平行四边形,所以GE
AF
AF
平面PEC,
GE
平面PEC
AF
平面PEC
思路二:通过构造三角形中位线,生成线线平行关系
(1)证法二:连接CE并延长交DA的延长线于点M,连接PM,在平行四边形ABCD中,
AB
CD,AD
CB,
AM
CB
点E是AB的中点,
点E是MC的中点
点A是MD的中点,又
点F是PD的中点
AF
PM
AF
平面PEC,PM
平面PEC,
AF
平面PEC
思路三:通过构造面面平行,生成线线平行关系
(1)证法三:取CD的中点Q,连接FQ,AQ,
点F是PD的中点,
QF
CP.
点Q是CD的中点,
CQ=
CD,
点E是AB的中点,
AE=
AB
,
在平行四边形ABCD中,
AB
CD,
AB=CD,
CQ
AE,CQ=AE
,
四边形AECQ是平行四边形,AQ
EC,
AQ
QF=Q,
平面AQF
平面PEC.
AF
平面AQF,
AF
平面PEC
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
PA=AD.求证:
(2)
AF
平面PCD
证明线面垂直的基本条件是什么?
(2)
证明线面平行,面面平行,需转化为证明线线平行
证明线面垂直,面面垂直,需转化为证明线线垂直
【题后反思】
线面平行
面面平行
线线平行
判定
性质
性质
判定
判定
性质
平行关系的转化
线面垂直
面面垂直
线线垂直
判定
定义
性质
判定
垂直关系的转化
【典型例题】
例1:如图,在正方体
中,
E是
中点,求证:
(1)
(2)
例1:如图,在正方体
中,
E是
中点,求证:
(1)
例1:如图,在正方体
中,
E是
中点,求证:
(2)
证明:
(1)
连接AC,交BD于点O,在正方体
中,
,
,
又
,
(2)
连接OE,因为E是
中点,又由(1)知,
O为AC中点,
,又OE
平面BDE,
,
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(1)
求证:
(2)
求证:
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(1)
求证:
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(2)
求证:
证明:
(1)
连接
,因为M,N分别为
,
的中点
,
,
,
,
(2)
在直三棱柱中,
所以侧面
为正方形,
则
又
,
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(1)
(2)
?
【典型例题】
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(1)
?
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(2)
?
【典型例题】
证明:
(1)连接OE,在正方形ABCD中,点O是AC的中点
E是PC的中点,
OE是
的中位线,
,又
,
(2)
在正方形ABCD中,
,
,
又
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(1)求证:
(2)求证:
(3)
若
求证:
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(1)求证:
面面平行
平行四边形
线面平行
线线平行
线面平行
中位线
线线平行
线面平行
证明:
(1)取CD的中点R,连接MR,NR
因为R,N分别是CD,PC的中点
所以
,又可证
因为NR与MR相交
可证
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(2)求证:
因为
,所以
在矩形ABCD中,
,又因为
,所以
,所以
,由(1)已证
,
所以
,
,又因为
所以
,所以
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(3)
若
求证:
H
(3)在
中,
所以
,连接PM,CM
所以
,又因为N是PC的中点,
于是
,由(2)知
所以
【典型例题】
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(1)
(2)
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(1)
证明:(1)取AB的中点M,连接FM,MC
因为F,M分别是BE,BA的中点
所以
,
因为AE,CD都和平面ABC垂直
所以
,所以
,又CD=
,
所以
所以四边形FMCD是平行四边形,所以
,
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(2)
(2)因为M是AB的中点,
是正三角形,所以
,
所以
因为F是BE的中点,
,所以
,又
,
所以,
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(1)
求证:
(2)当点M为BD的中点时,求证:
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(1)
求证:
证明:
(1)因为
所以
,所以
又
,
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(2)当点M为BD的中点时,求证:
(2)连接DF与EC交于点N,则N为DF的中点
因为M是BD的中点,所以
又
所以
【课后练习】
练习1:如图,已知三棱锥A-BPC中,
M为AB中点,D为PB中点,且
为正三角形
(1)求证:
(2)求证:
练习2.如图,三棱柱
中,侧棱
,
为等腰直角三角形,
,D,E,F分别是
的中点.
(1)求证:
(2)求证:
(3)设AB=
,求三棱锥D-AEF的体积
【方法小结】
将空间位置关系转化成平面内的位置关系
将图形语言、文字语言转化成符号语言
将平行、垂直关系转化为线线平行、线线垂直
高一年级
数学
空间中平行和垂直的综合应用(一)
高一年级
数学
空间中平行和垂直的综合应用(一)
证明线面平行、线面垂直有哪些方法?
证明面面平行、面面垂直有哪些方法?
【知识回顾】
【知识回顾】
线面平行的判定定理
线面平行的性质定理
【知识回顾】
面面平行的判定定理
面面平行的判定定理推论
c
d
【知识回顾】
面面平行的性质定理
【知识回顾】
线面垂直的判定定理
线面垂直的性质定理
【知识回顾】
面面垂直的判定定理
面面垂直的性质定理
平行与垂直的相互转化
垂直于同一个平面的两条直线平行,即
与平面的垂线平行的直线也垂直于这个平面,
即
通过前面几节课的学习,我们认识了空间中的点、线、面的位置关系,重点学习了空间中的平行关系和垂直关系,这节课我们将探究空间中平行和垂直的综合应用问题,进一步提升解决立体几何综合问题的能力.
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
【真题面对面】
PA=AD.求证:
(1)AF
平面PEC
(2)
AF
平面PCD
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
PA=AD.求证:
(1)AF
平面PEC
思路一:通过构造平行四边形生成线线平行关系
(1)证法一:取PC的中点G,连接EG,FG
点F是PD的中点,
GF
CD,GF=
CD
点E是AB的中点,
EA=
AB
在平行四边形ABCD中,AB
CD,AB=CD
GF
AE,GF=AE,
四边形AEGF是平行四边形,所以GE
AF
AF
平面PEC,
GE
平面PEC
AF
平面PEC
思路二:通过构造三角形中位线,生成线线平行关系
(1)证法二:连接CE并延长交DA的延长线于点M,连接PM,在平行四边形ABCD中,
AB
CD,AD
CB,
AM
CB
点E是AB的中点,
点E是MC的中点
点A是MD的中点,又
点F是PD的中点
AF
PM
AF
平面PEC,PM
平面PEC,
AF
平面PEC
思路三:通过构造面面平行,生成线线平行关系
(1)证法三:取CD的中点Q,连接FQ,AQ,
点F是PD的中点,
QF
CP.
点Q是CD的中点,
CQ=
CD,
点E是AB的中点,
AE=
AB
,
在平行四边形ABCD中,
AB
CD,
AB=CD,
CQ
AE,CQ=AE
,
四边形AECQ是平行四边形,AQ
EC,
AQ
QF=Q,
平面AQF
平面PEC.
AF
平面AQF,
AF
平面PEC
1.如图,四棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,
PA=AD.求证:
(2)
AF
平面PCD
证明线面垂直的基本条件是什么?
(2)
证明线面平行,面面平行,需转化为证明线线平行
证明线面垂直,面面垂直,需转化为证明线线垂直
【题后反思】
线面平行
面面平行
线线平行
判定
性质
性质
判定
判定
性质
平行关系的转化
线面垂直
面面垂直
线线垂直
判定
定义
性质
判定
垂直关系的转化
【典型例题】
例1:如图,在正方体
中,
E是
中点,求证:
(1)
(2)
例1:如图,在正方体
中,
E是
中点,求证:
(1)
例1:如图,在正方体
中,
E是
中点,求证:
(2)
证明:
(1)
连接AC,交BD于点O,在正方体
中,
,
,
又
,
(2)
连接OE,因为E是
中点,又由(1)知,
O为AC中点,
,又OE
平面BDE,
,
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(1)
求证:
(2)
求证:
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(1)
求证:
同类练习1:直三棱柱
中,
M为
的中点,N是
与
的交点.
(2)
求证:
证明:
(1)
连接
,因为M,N分别为
,
的中点
,
,
,
,
(2)
在直三棱柱中,
所以侧面
为正方形,
则
又
,
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(1)
(2)
?
【典型例题】
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(1)
?
例2:如图所示,O是正方形ABCD的中心,
,
E是PC的中点,求证:
(2)
?
【典型例题】
证明:
(1)连接OE,在正方形ABCD中,点O是AC的中点
E是PC的中点,
OE是
的中位线,
,又
,
(2)
在正方形ABCD中,
,
,
又
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(1)求证:
(2)求证:
(3)
若
求证:
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(1)求证:
面面平行
平行四边形
线面平行
线线平行
线面平行
中位线
线线平行
线面平行
证明:
(1)取CD的中点R,连接MR,NR
因为R,N分别是CD,PC的中点
所以
,又可证
因为NR与MR相交
可证
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(2)求证:
因为
,所以
在矩形ABCD中,
,又因为
,所以
,所以
,由(1)已证
,
所以
,
,又因为
所以
,所以
同类练习2:如图,PA
矩形ABCD所在的平面,M,N分别是AB,PC的中点
(3)
若
求证:
H
(3)在
中,
所以
,连接PM,CM
所以
,又因为N是PC的中点,
于是
,由(2)知
所以
【典型例题】
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(1)
(2)
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(1)
证明:(1)取AB的中点M,连接FM,MC
因为F,M分别是BE,BA的中点
所以
,
因为AE,CD都和平面ABC垂直
所以
,所以
,又CD=
,
所以
所以四边形FMCD是平行四边形,所以
,
例3:如图,已知
是正三角形,EA,CD都垂直于平面ACB,且EA=AB=
,DC=
,
F是BE的中点,求证:
(2)
(2)因为M是AB的中点,
是正三角形,所以
,
所以
因为F是BE的中点,
,所以
,又
,
所以,
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(1)
求证:
(2)当点M为BD的中点时,求证:
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(1)
求证:
证明:
(1)因为
所以
,所以
又
,
同类练习3:在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,
(2)当点M为BD的中点时,求证:
(2)连接DF与EC交于点N,则N为DF的中点
因为M是BD的中点,所以
又
所以
【课后练习】
练习1:如图,已知三棱锥A-BPC中,
M为AB中点,D为PB中点,且
为正三角形
(1)求证:
(2)求证:
练习2.如图,三棱柱
中,侧棱
,
为等腰直角三角形,
,D,E,F分别是
的中点.
(1)求证:
(2)求证:
(3)设AB=
,求三棱锥D-AEF的体积
【方法小结】
将空间位置关系转化成平面内的位置关系
将图形语言、文字语言转化成符号语言
将平行、垂直关系转化为线线平行、线线垂直
高一年级
数学
空间中平行和垂直的综合应用(一)
