高一数学(人教B版)-空间中的平行和垂直的综合应用(二)-课件(55张PPT)
文档属性
| 名称 | 高一数学(人教B版)-空间中的平行和垂直的综合应用(二)-课件(55张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 20:00:24 | ||
图片预览








文档简介
(共55张PPT)
高一年级
数学
空间中平行和垂直的综合应用(二)
上节课,我们借助不同类型的空间几何体,例如,从棱柱、棱锥及其他组合体中观察线面位置关系,结合有关定理,进行证明或者计算.
这节课,我们将聚焦于不同呈现形式的问题,继续探究空间中的平行和垂直关系,进一步提升解题能力.
【学习聚焦】
【问题聚焦】
类型一
空间点、线、面位置关系的判断
类型二
空间平行、垂直关系的证明
类型三
折叠问题
类型四
空间位置关系的探索性问题
空间点、线、面位置关系的判断
【类型一】
空间平行、垂直关系判断的主要方法有:
借助定理进行证明
借助常见几何体的性质进行判断
反证法
空间点、线、面位置关系的判断
【类型一】
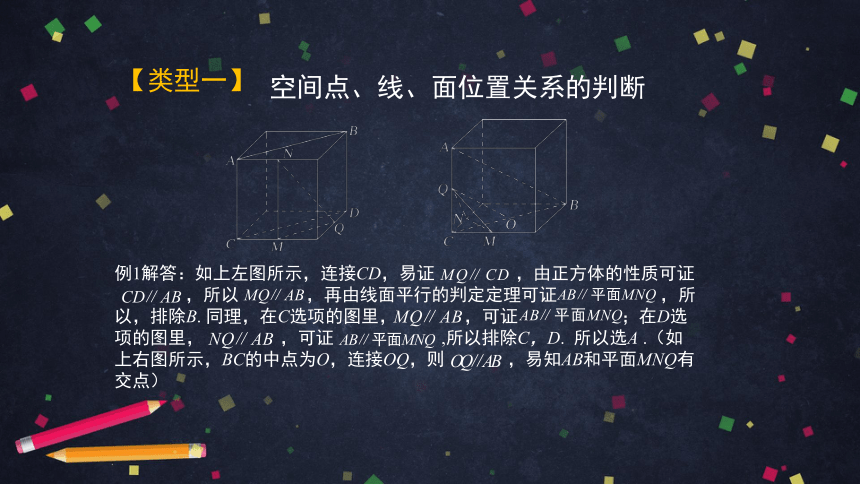
例1:如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
空间点、线、面位置关系的判断
【类型一】
例1解答:如上左图所示,连接CD,易证
,由正方体的性质可证
所以
,再由线面平行的判定定理可证
,所以,排除B.
同理,在C选项的图里,
,可证
;在D选项的图里,
,可证
,所以排除C,D.
所以选A
.(如上右图所示,BC的中点为O,连接OQ,则
,易知AB和平面MNQ有交点)
?
空间点、线、面位置关系的判断
【类型一】
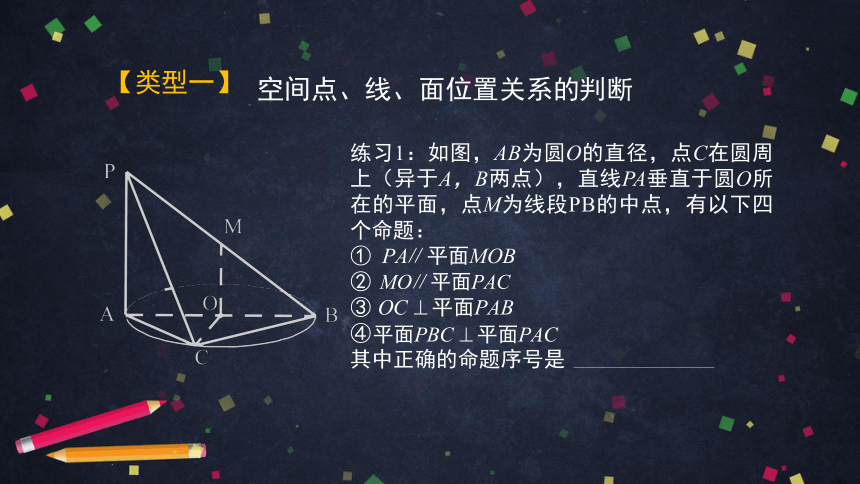
练习1:如图,AB为圆O的直径,点C在圆周上(异于A,B两点),直线PA垂直于圆O所在的平面,点M为线段PB的中点,有以下四个命题:
①
②
③
④
其中正确的命题序号是
空间点、线、面位置关系的判断
【类型一】
答案:②
④
练1解答:因为O在AB上,M在PB上,所以
,故①错;
因为MO是
的中位线,所以
,
易证
,故②正确;
因为OC不一定垂直AB,所以③错;因为
,所以
,因为AB是圆O的直径,所以
,又
,所以
,
,所以
,故④正确
解决空间点、线、面位置关系的组合判断题,主要是根据平面的基本性质、以及空间平行、垂直关系的判定定理和性质定理进行判断,同时借助特殊几何体如正方体、长方体、直棱柱、正棱锥等几何模型的性质挖掘隐含条件.
【类型一方法小结】
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系证明的主要思想是转化,即通过判定定理、性质定理将线线、线面、面面之间的平行、垂直关系相互转化.
空间平行、垂直关系的证明
【类型二】
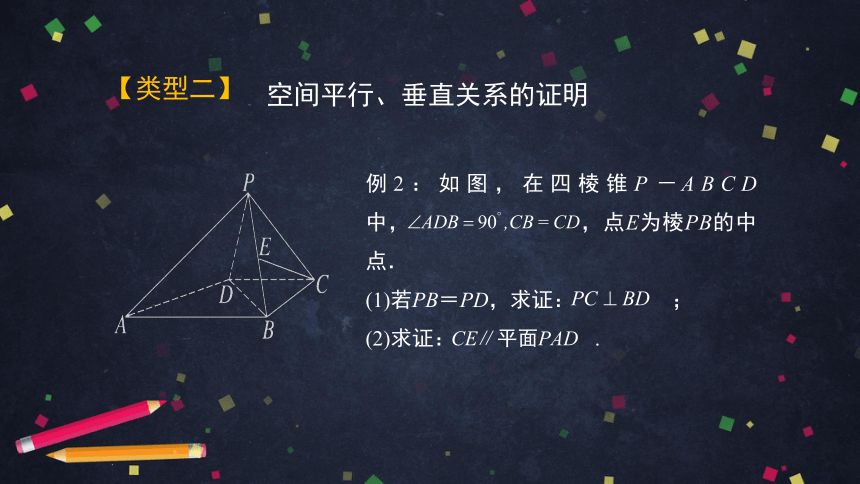
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(1)若PB=PD,求证:
;
(2)求证:
.
空间平行、垂直关系的证明
【类型二】
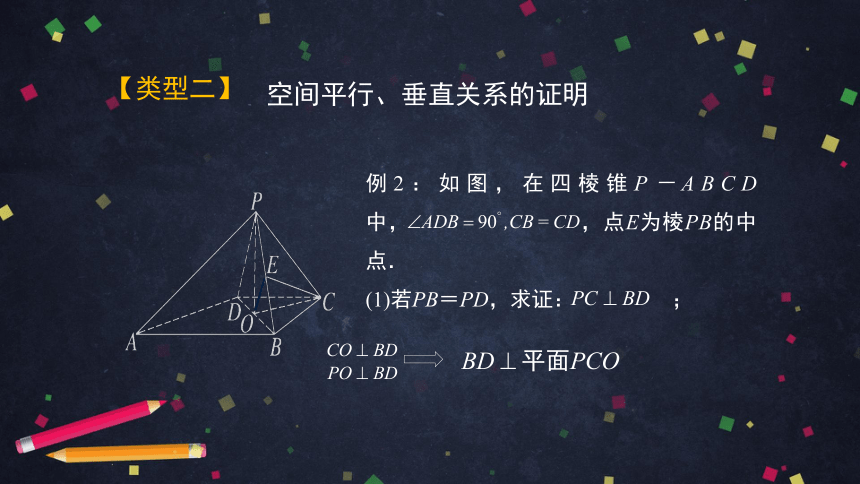
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(1)若PB=PD,求证:
;
例2解答:
证明: (1)取BD的中点O,连接CO,PO,
因为CD=CB,所以
为等腰三角形,
所以
.
因为PB=PD,所以
为等腰三角形,
所以
.又
,
所以
.
所以
.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(2)求证:
.
例2解答:
证明:(2)由E为PB的中点,连接EO,则
,
由
,可得
,
所以
,
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(1)求证:
;
(2)
与线段AB交于点M,指出点M的位置,说明理由.
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(1)求证:
;
BE∥FG
练2解答
(1)证明 取
的中点G,连接EG,FG,
∵点E为
的中点,∴EG
,且EG=
,
∵F为BC中点,
∴
且
,
∴
BF∥EG且BF=EG.所以四边形BFGE是平行四边形,
所以BE∥FG,又BE
平面
,FG
平面
,
所以直线BE∥平面
.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(2)
与线段AB交于点M,指出点M的位置,说明理由.
AC∥FM
练2解答:(2) M为棱AB的中点.
理由如下:
因为AC∥
,
平面
,
平面
,
所以直线AC∥平面
,
又平面
∩平面ABC=FM,
所以AC∥FM.
又F为棱BC的中点,所以M为棱AB的中点.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
证明平行关系的核心任务是证明线线平行:
证明线线平行常用的方法:
公理4:两直线同时和第三条直线平行,这两条直线平行
平行四边形对边平行
利用三角形的中位线定理(或线段成比例)证明线线平行
利用线面平行、面面平行的性质定理证明线线平行
【类型二方法小结】
证明垂直关系的核心任务是证明线线垂直:
证明线线垂直常用的方法:
勾股定理
长方形邻边互相垂直,菱形对角线互相垂直
等腰三角形底边中线即高线的性质
利用线面垂直的定义,要证线线垂直,只需证明一条直线垂直于另一条直线所在的平面即可
【类型二方法小结】
折叠问题
【类型三】
平面图形经过翻折成为空间图形后,原有的点、线、面位置关系和数量关系,有的发生了改变,有的没有改变,所以,确认折叠前后的“不变”和“改变”是什么,是解决问题的关键.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(1)求证:
;
(2)求证:
;
(3)在线段PD,BC上是否分别存在点M,N,使得
?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(1)求证:
;
例3解答:
(1)证明 折叠前,因为四边形AECD为菱形,所以
,
所以折叠后,
,又
,
所以
.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(2)求证:
;
例3解答:
(2)证明 因为四边形AECD为菱形,所以
.
又点E为AB的中点,所以
,
所以四边形DEBC为平行四边形,所以
.
又由(1)得,
,所以
.
因为
,所以
.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(3)在线段PD,BC上是否分别存在点M,N,使得
?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.
例3解答:
(3)解 存在满足条件的点M,N,且M,N分别是PD和BC的中点.
如图,分别取PD和BC的中点M,N.连接EN,PN,MF,CM.
因为四边形DEBC为平行四边形,所以
,
所以四边形ENCF为平行四边形,所以
.
在
中,M,F分别为PD,DE的中点,所以
.
又
,
,所以
.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(1)证明:
;
(2)求三棱锥E-ACD的体积.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(1)证明:
;
练3解答:(1)证明 连接BE交AF于点O,取AC的中点H,连接OH,DH,则OH是
的中位线,
所以
,
由已知得
,
所以
,
所以四边形DEOH为平行四边形,
,
又因为
,
所以
.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(2)求三棱锥E-ACD的体积.
练3解答:(2)解 由已知得,四边形ABFE为正方形,且边长为2,
则
,由已知
,
,
,
又
,
,
,则四边形DEFC是直角梯形,
又
,
所以
,所以AE是三棱锥A-DEC的高,
【类型三方法小结】
解决翻折问题的关键,就是要认真审题,分析清楚翻折前后位置关系以及数量关系的改变和不变,根据这些,去完成翻折后生成的几何体中的证明和计算.
【类型四】
空间位置关系的探索性问题
立体几何中的探索性问题主要是对平行、垂直关系的探究,对条件和结论不完备的开放性问题的探究,这类问题的一般设问方式是“是否存在?存在给出证明,不存在说明理由”.解决这类问题,一般根据设问,首先假设其存在,然后在这个假设下进行推理论证,如果得到了合乎情理的结论就肯定假设,得到了矛盾就否定假设。
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(1)求证:
;
(2)
上是否存一点P,使得DP与
以及
都平行?证明你的结论.
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(1)求证:
;
B
A
D
C
例4解答:证明
(1)直棱柱
中,
,
∴
,又∵
AB=2AD=2CD=2,由平面几何及余弦定理
∴
又
【类型四】
空间位置关系的探索性问题
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(2)
上是否存一点P,使得DP与
与
都平行?证明你的结论.
P
例4解答:(2)存在点P,P为
的中点。
证明:由P为
的中点,有
又
∴
四边形
为平行四边形,从而
又
同理,
【类型四】
空间位置关系的探索性问题
P
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(1)求证:
(2)求证:
(3)试问:在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(1)求证:
(2)求证:
练4解答:(1)因为点E是AC中点,点D为PA中点所以DE为三角形PAC的中位线,所以
,又因为
,所以
(2)因为
又
,所以
,
,所以
,又因为
,且
,所以
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(3)试问:在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
练4解答:(3)答
当点F是线段AB中点时,过点D,E,F的平面内的任一条直线都与平面PBC平行
取AB中点F,连接EF,DF,由(1)可知
DE
平面PBC因为点E是AC中点,点F为AB的中点所以EF为
的中位线,所以
,又因为
,所以
又因为
所以
,所以
内的任一条直线都与
平行
【类型四方法小结】
对于存在判断型问题,解题的策略一般为:
先假设存在
猜想某个特殊位置会满足条件,然后再尝试证明
利用条件推理论证说明存在
1.如图,四棱锥P-ABCD中,
,底面ABCD是正方形,则下列结论:
①
②
③
④
其中正确的结论序号是
【课后练习】
2.如图,在平行四边形ABCM中,
AB=AC=3,
.以AC为折痕将
折起,使点M到达点D的位置,且
.
(1)证明:
;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=
,求三棱锥Q-?ABP的体积.
【课后练习】
3.如图,在矩形ABCD中,AB=2AD,M为CD的中点,将
沿AM折起,使得平面ADM
平面ABCM,点O是线段AM的中点
(1)求证:
(2)求证:
(3)过D点是否存在一条直线
,同时满足以下两个条件:
平面BCD
请说明理由
【课后练习】
【课后小结】
处理空间平行和垂直关系,经常要把问题转化成基本的线线关系,根据定理的要求找齐线线关系的条件,完成判断或者证明
处理平面图形的折叠问题,要根据折叠前后的改变量和不变量完成证明或者计算
处理探索性或者存在性问题,要从不同的角度找到问题的突破口,既可以从条件入手,也可以从结论入手,把问题转化成常规的证明或者计算
高一年级
数学
空间中平行和垂直的综合应用(二)
主讲人
黄
悦
北师大二附中
高一年级
数学
空间中平行和垂直的综合应用(二)
上节课,我们借助不同类型的空间几何体,例如,从棱柱、棱锥及其他组合体中观察线面位置关系,结合有关定理,进行证明或者计算.
这节课,我们将聚焦于不同呈现形式的问题,继续探究空间中的平行和垂直关系,进一步提升解题能力.
【学习聚焦】
【问题聚焦】
类型一
空间点、线、面位置关系的判断
类型二
空间平行、垂直关系的证明
类型三
折叠问题
类型四
空间位置关系的探索性问题
空间点、线、面位置关系的判断
【类型一】
空间平行、垂直关系判断的主要方法有:
借助定理进行证明
借助常见几何体的性质进行判断
反证法
空间点、线、面位置关系的判断
【类型一】
例1:如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
空间点、线、面位置关系的判断
【类型一】
例1解答:如上左图所示,连接CD,易证
,由正方体的性质可证
所以
,再由线面平行的判定定理可证
,所以,排除B.
同理,在C选项的图里,
,可证
;在D选项的图里,
,可证
,所以排除C,D.
所以选A
.(如上右图所示,BC的中点为O,连接OQ,则
,易知AB和平面MNQ有交点)
?
空间点、线、面位置关系的判断
【类型一】
练习1:如图,AB为圆O的直径,点C在圆周上(异于A,B两点),直线PA垂直于圆O所在的平面,点M为线段PB的中点,有以下四个命题:
①
②
③
④
其中正确的命题序号是
空间点、线、面位置关系的判断
【类型一】
答案:②
④
练1解答:因为O在AB上,M在PB上,所以
,故①错;
因为MO是
的中位线,所以
,
易证
,故②正确;
因为OC不一定垂直AB,所以③错;因为
,所以
,因为AB是圆O的直径,所以
,又
,所以
,
,所以
,故④正确
解决空间点、线、面位置关系的组合判断题,主要是根据平面的基本性质、以及空间平行、垂直关系的判定定理和性质定理进行判断,同时借助特殊几何体如正方体、长方体、直棱柱、正棱锥等几何模型的性质挖掘隐含条件.
【类型一方法小结】
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系证明的主要思想是转化,即通过判定定理、性质定理将线线、线面、面面之间的平行、垂直关系相互转化.
空间平行、垂直关系的证明
【类型二】
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(1)若PB=PD,求证:
;
(2)求证:
.
空间平行、垂直关系的证明
【类型二】
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(1)若PB=PD,求证:
;
例2解答:
证明: (1)取BD的中点O,连接CO,PO,
因为CD=CB,所以
为等腰三角形,
所以
.
因为PB=PD,所以
为等腰三角形,
所以
.又
,
所以
.
所以
.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
例2:如图,在四棱锥P-ABCD中,
,点E为棱PB的中点.
(2)求证:
.
例2解答:
证明:(2)由E为PB的中点,连接EO,则
,
由
,可得
,
所以
,
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(1)求证:
;
(2)
与线段AB交于点M,指出点M的位置,说明理由.
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(1)求证:
;
BE∥FG
练2解答
(1)证明 取
的中点G,连接EG,FG,
∵点E为
的中点,∴EG
,且EG=
,
∵F为BC中点,
∴
且
,
∴
BF∥EG且BF=EG.所以四边形BFGE是平行四边形,
所以BE∥FG,又BE
平面
,FG
平面
,
所以直线BE∥平面
.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
练2:如图,三棱柱
的各棱长均为2,
,E,F分别为棱
的中点.
(2)
与线段AB交于点M,指出点M的位置,说明理由.
AC∥FM
练2解答:(2) M为棱AB的中点.
理由如下:
因为AC∥
,
平面
,
平面
,
所以直线AC∥平面
,
又平面
∩平面ABC=FM,
所以AC∥FM.
又F为棱BC的中点,所以M为棱AB的中点.
空间平行、垂直关系的证明
【类型二】
空间平行、垂直关系的证明
【类型二】
证明平行关系的核心任务是证明线线平行:
证明线线平行常用的方法:
公理4:两直线同时和第三条直线平行,这两条直线平行
平行四边形对边平行
利用三角形的中位线定理(或线段成比例)证明线线平行
利用线面平行、面面平行的性质定理证明线线平行
【类型二方法小结】
证明垂直关系的核心任务是证明线线垂直:
证明线线垂直常用的方法:
勾股定理
长方形邻边互相垂直,菱形对角线互相垂直
等腰三角形底边中线即高线的性质
利用线面垂直的定义,要证线线垂直,只需证明一条直线垂直于另一条直线所在的平面即可
【类型二方法小结】
折叠问题
【类型三】
平面图形经过翻折成为空间图形后,原有的点、线、面位置关系和数量关系,有的发生了改变,有的没有改变,所以,确认折叠前后的“不变”和“改变”是什么,是解决问题的关键.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(1)求证:
;
(2)求证:
;
(3)在线段PD,BC上是否分别存在点M,N,使得
?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(1)求证:
;
例3解答:
(1)证明 折叠前,因为四边形AECD为菱形,所以
,
所以折叠后,
,又
,
所以
.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(2)求证:
;
例3解答:
(2)证明 因为四边形AECD为菱形,所以
.
又点E为AB的中点,所以
,
所以四边形DEBC为平行四边形,所以
.
又由(1)得,
,所以
.
因为
,所以
.
例3:如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将
沿线段DE折起到
的位置,如图2所示.
折叠问题
【类型三】
(3)在线段PD,BC上是否分别存在点M,N,使得
?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.
例3解答:
(3)解 存在满足条件的点M,N,且M,N分别是PD和BC的中点.
如图,分别取PD和BC的中点M,N.连接EN,PN,MF,CM.
因为四边形DEBC为平行四边形,所以
,
所以四边形ENCF为平行四边形,所以
.
在
中,M,F分别为PD,DE的中点,所以
.
又
,
,所以
.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(1)证明:
;
(2)求三棱锥E-ACD的体积.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(1)证明:
;
练3解答:(1)证明 连接BE交AF于点O,取AC的中点H,连接OH,DH,则OH是
的中位线,
所以
,
由已知得
,
所以
,
所以四边形DEOH为平行四边形,
,
又因为
,
所以
.
练3:在梯形ABCD中(如图1),AB∥CD,AB=2,CD=5,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=2,将梯形ABCD沿AE,BF同侧折起,使得
,得到空间几何体(如图2).
折叠问题
【类型三】
(2)求三棱锥E-ACD的体积.
练3解答:(2)解 由已知得,四边形ABFE为正方形,且边长为2,
则
,由已知
,
,
,
又
,
,
,则四边形DEFC是直角梯形,
又
,
所以
,所以AE是三棱锥A-DEC的高,
【类型三方法小结】
解决翻折问题的关键,就是要认真审题,分析清楚翻折前后位置关系以及数量关系的改变和不变,根据这些,去完成翻折后生成的几何体中的证明和计算.
【类型四】
空间位置关系的探索性问题
立体几何中的探索性问题主要是对平行、垂直关系的探究,对条件和结论不完备的开放性问题的探究,这类问题的一般设问方式是“是否存在?存在给出证明,不存在说明理由”.解决这类问题,一般根据设问,首先假设其存在,然后在这个假设下进行推理论证,如果得到了合乎情理的结论就肯定假设,得到了矛盾就否定假设。
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(1)求证:
;
(2)
上是否存一点P,使得DP与
以及
都平行?证明你的结论.
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(1)求证:
;
B
A
D
C
例4解答:证明
(1)直棱柱
中,
,
∴
,又∵
AB=2AD=2CD=2,由平面几何及余弦定理
∴
又
【类型四】
空间位置关系的探索性问题
【类型四】
空间位置关系的探索性问题
例4:直棱柱
底面ABCD是直角梯形,
,AB=2AD=2CD=2.
(2)
上是否存一点P,使得DP与
与
都平行?证明你的结论.
P
例4解答:(2)存在点P,P为
的中点。
证明:由P为
的中点,有
又
∴
四边形
为平行四边形,从而
又
同理,
【类型四】
空间位置关系的探索性问题
P
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(1)求证:
(2)求证:
(3)试问:在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(1)求证:
(2)求证:
练4解答:(1)因为点E是AC中点,点D为PA中点所以DE为三角形PAC的中位线,所以
,又因为
,所以
(2)因为
又
,所以
,
,所以
,又因为
,且
,所以
【类型四】
空间位置关系的探索性问题
练4:如图在三棱锥P-ABC中,
.设D,E分别为PA,AC中点
(3)试问:在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
练4解答:(3)答
当点F是线段AB中点时,过点D,E,F的平面内的任一条直线都与平面PBC平行
取AB中点F,连接EF,DF,由(1)可知
DE
平面PBC因为点E是AC中点,点F为AB的中点所以EF为
的中位线,所以
,又因为
,所以
又因为
所以
,所以
内的任一条直线都与
平行
【类型四方法小结】
对于存在判断型问题,解题的策略一般为:
先假设存在
猜想某个特殊位置会满足条件,然后再尝试证明
利用条件推理论证说明存在
1.如图,四棱锥P-ABCD中,
,底面ABCD是正方形,则下列结论:
①
②
③
④
其中正确的结论序号是
【课后练习】
2.如图,在平行四边形ABCM中,
AB=AC=3,
.以AC为折痕将
折起,使点M到达点D的位置,且
.
(1)证明:
;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=
,求三棱锥Q-?ABP的体积.
【课后练习】
3.如图,在矩形ABCD中,AB=2AD,M为CD的中点,将
沿AM折起,使得平面ADM
平面ABCM,点O是线段AM的中点
(1)求证:
(2)求证:
(3)过D点是否存在一条直线
,同时满足以下两个条件:
平面BCD
请说明理由
【课后练习】
【课后小结】
处理空间平行和垂直关系,经常要把问题转化成基本的线线关系,根据定理的要求找齐线线关系的条件,完成判断或者证明
处理平面图形的折叠问题,要根据折叠前后的改变量和不变量完成证明或者计算
处理探索性或者存在性问题,要从不同的角度找到问题的突破口,既可以从条件入手,也可以从结论入手,把问题转化成常规的证明或者计算
高一年级
数学
空间中平行和垂直的综合应用(二)
主讲人
黄
悦
北师大二附中
