苏科版九下数学 5.2.4y=ax^2+bx+c的图像 学案 (无答案)
文档属性
| 名称 | 苏科版九下数学 5.2.4y=ax^2+bx+c的图像 学案 (无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 39.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
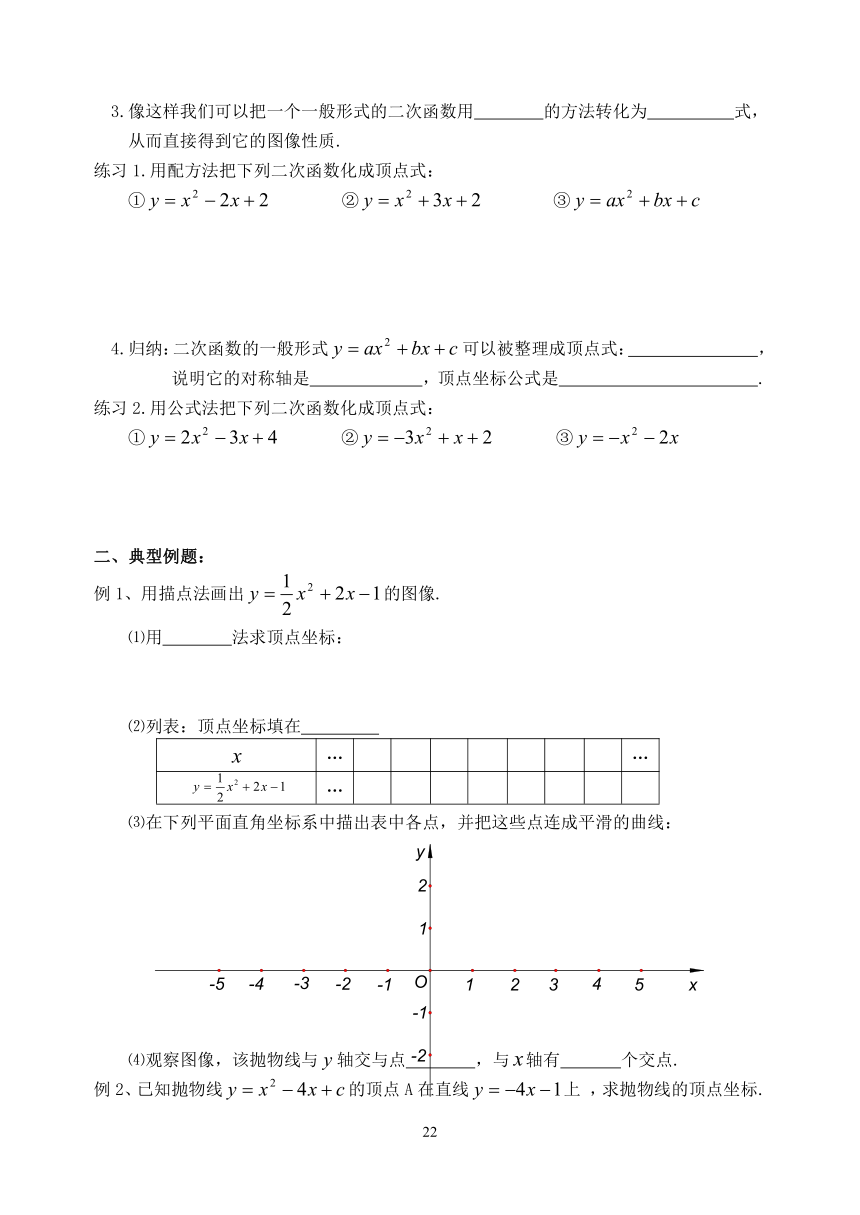
图片预览

文档简介
5.2二次函数的图像与性质(5)
班级______学号_____姓名___________
【学习目标】
1.会用描点法画二次函数的图像,掌握它的性质.
2.渗透数形结合思想.
【学前准备】
1.
根据的图像和性质填表:
函
数
图
像
开口
对称轴
顶
点
增
减
性
向上
当
时,随的增大而减少.当时,随的增大而
.
当
时,随的增大而减少.当
时,随的增大而
.
2.抛物线的开口向
,对称轴是
;顶点坐标是
,
说明当=
时,y有最
值是
;无论取任何实数,的取值范围是
.
3.抛物线的开口向
,对称轴是
;顶点坐标是
,
说明当=
时,y有最
值是
;无论取任何实数,的取值范围是
.
4.抛物线与抛物线
关于轴成轴对称;抛物线
与抛物线
关于轴成轴对称.
5.被我们称为二次函数的
式.
【合作探究】
一、探索归纳:
1.问题:你能直接说出函数
的图像的对称轴和顶点坐标吗?
2.你有办法解决问题①吗?
的对称轴是
,顶点坐标是
.
3.像这样我们可以把一个一般形式的二次函数用
的方法转化为
式,
从而直接得到它的图像性质.
练习1.用配方法把下列二次函数化成顶点式:
①
②
③
4.归纳:二次函数的一般形式可以被整理成顶点式:
,
说明它的对称轴是
,顶点坐标公式是
.
练习2.用公式法把下列二次函数化成顶点式:
①
②
③
二、典型例题:
例1、用描点法画出的图像.
⑴用
法求顶点坐标:
⑵列表:顶点坐标填在
…
…
…
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察图像,该抛物线与轴交与点
,与轴有
个交点.
例2、已知抛物线的顶点A在直线上
,求抛物线的顶点坐标.
【课堂检测】
1.用配方法把下列二次函数化成顶点式:
①
②
2.用公式法把下列二次函数化成顶点式:
①
②
3.用描点法画出的图像.
⑴用
法求顶点坐标:
…
…
…
⑵列表:
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察左图:
①抛物线与轴交点坐标是
;
②抛物线与轴交点坐标是
;
③当
时,;
④它的对称轴是
;
⑤当
时,随的增大而减小.
【课外作业】
1.用配方法把下列二次函数化成顶点式:
①
②
2.用公式法把下列二次函数化成顶点式:
①
②
3.抛物线y=
3x2+2x的图像开口向
,顶点坐标是
,说明当x=
时,
y有最
值是
.
4.函数y=-2x2+8x+8的对称轴是
,当x
时,y随x的增大而增大.
5.用描点法画出的图像.
⑴用
法求顶点坐标:
…
…
…
⑵列表:
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察左图:
①抛物线与轴交点坐标是
;
抛物线与轴交点坐标是
;
②当
时,;
③它的对称轴是
;
④当
时,随的增大而减小.
PAGE
24
班级______学号_____姓名___________
【学习目标】
1.会用描点法画二次函数的图像,掌握它的性质.
2.渗透数形结合思想.
【学前准备】
1.
根据的图像和性质填表:
函
数
图
像
开口
对称轴
顶
点
增
减
性
向上
当
时,随的增大而减少.当时,随的增大而
.
当
时,随的增大而减少.当
时,随的增大而
.
2.抛物线的开口向
,对称轴是
;顶点坐标是
,
说明当=
时,y有最
值是
;无论取任何实数,的取值范围是
.
3.抛物线的开口向
,对称轴是
;顶点坐标是
,
说明当=
时,y有最
值是
;无论取任何实数,的取值范围是
.
4.抛物线与抛物线
关于轴成轴对称;抛物线
与抛物线
关于轴成轴对称.
5.被我们称为二次函数的
式.
【合作探究】
一、探索归纳:
1.问题:你能直接说出函数
的图像的对称轴和顶点坐标吗?
2.你有办法解决问题①吗?
的对称轴是
,顶点坐标是
.
3.像这样我们可以把一个一般形式的二次函数用
的方法转化为
式,
从而直接得到它的图像性质.
练习1.用配方法把下列二次函数化成顶点式:
①
②
③
4.归纳:二次函数的一般形式可以被整理成顶点式:
,
说明它的对称轴是
,顶点坐标公式是
.
练习2.用公式法把下列二次函数化成顶点式:
①
②
③
二、典型例题:
例1、用描点法画出的图像.
⑴用
法求顶点坐标:
⑵列表:顶点坐标填在
…
…
…
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察图像,该抛物线与轴交与点
,与轴有
个交点.
例2、已知抛物线的顶点A在直线上
,求抛物线的顶点坐标.
【课堂检测】
1.用配方法把下列二次函数化成顶点式:
①
②
2.用公式法把下列二次函数化成顶点式:
①
②
3.用描点法画出的图像.
⑴用
法求顶点坐标:
…
…
…
⑵列表:
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察左图:
①抛物线与轴交点坐标是
;
②抛物线与轴交点坐标是
;
③当
时,;
④它的对称轴是
;
⑤当
时,随的增大而减小.
【课外作业】
1.用配方法把下列二次函数化成顶点式:
①
②
2.用公式法把下列二次函数化成顶点式:
①
②
3.抛物线y=
3x2+2x的图像开口向
,顶点坐标是
,说明当x=
时,
y有最
值是
.
4.函数y=-2x2+8x+8的对称轴是
,当x
时,y随x的增大而增大.
5.用描点法画出的图像.
⑴用
法求顶点坐标:
…
…
…
⑵列表:
⑶在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:
⑷观察左图:
①抛物线与轴交点坐标是
;
抛物线与轴交点坐标是
;
②当
时,;
③它的对称轴是
;
④当
时,随的增大而减小.
PAGE
24
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
