苏科版九下数学 5.2二次函数的图象与性质教案
文档属性
| 名称 | 苏科版九下数学 5.2二次函数的图象与性质教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 00:00:00 | ||
图片预览

文档简介
二次函数的图象与性质(一)
一、教学目标?
1.会用描点法画y=ax函数的图象.?
2.结合y=ax图象初步理解抛物线的开口方向,对称轴,顶点坐标,及二次函数的性质.?
二、教学重点、难点及教学突破?
(一)教学重点?
1.通过列表、描点、连线画函数y=ax图象.?
2.通过图象初步理解二次函数性质;
3.二次函数性质的简单应用.
(二)教学难点?
结合图象理解抛物线开口方向、对称轴、顶点坐标及基本性质,并进行归纳总结.?
(三)教学突破?
有“一次函数”画图象的基础,在画图象的基本方法上学生问题不会太大,但教师应结合列表的数据引导学生对抛物线图象大致趋势的理解.学生在结合图象观察、体会性质时会有一些困难,教师应大胆让学生自己发现,归纳,鼓励学生讨论,交流.通过学生间相互的取长补短最终能突破重难点.?
三、教学过程?
(一)复习引入?
知识回顾:
引入课题:二次函数的图象与性质(一)
(二)探索实践
在直角坐标系⑴中画出二次函数y=x2的图象
x
…
…
y=x2
…
…
图⑴
图⑵
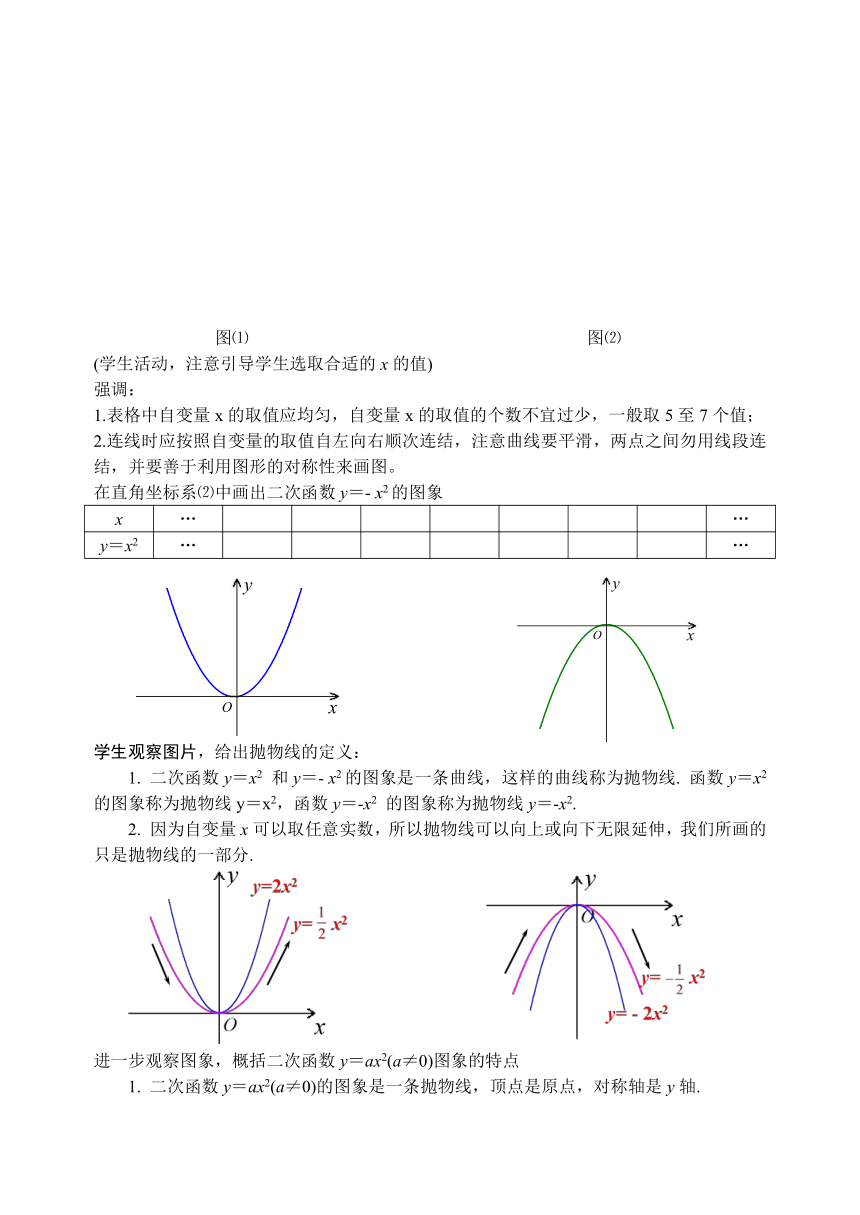
(学生活动,注意引导学生选取合适的x的值)
强调:
1.表格中自变量x的取值应均匀,自变量x的取值的个数不宜过少,一般取5至7个值;
2.连线时应按照自变量的取值自左向右顺次连结,注意曲线要平滑,两点之间勿用线段连结,并要善于利用图形的对称性来画图。
在直角坐标系⑵中画出二次函数y=-
x2的图象
x
…
…
y=x2
…
…
学生观察图片,给出抛物线的定义:
1.
二次函数y=x2
和y=-
x2的图象是一条曲线,这样的曲线称为抛物线.
函数y=x2
的图象称为抛物线y=x2,函数y=-x2
的图象称为抛物线y=-x2.
2.
因为自变量x可以取任意实数,所以抛物线可以向上或向下无限延伸,我们所画的只是抛物线的一部分.
进一步观察图象,概括二次函数y=ax2(a≠0)图象的特点
1.
二次函数y=ax2(a≠0)的图象是一条抛物线,顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2的开口向上,在对称轴的左侧,曲线自左向右下降,在对称轴的右侧,图象自左向右上升,顶点位于抛物线的最低处;
3.当a
<0时,抛物线y=ax2的开口向下,在对称轴的左侧,曲线自左向右上升,在对称轴的右侧,图象自左向右下降,顶点位于抛物线的最高处;
(分类思想在数学学习中的应用)
根据图象的特点,分析二次函数的性质(可与一次函数和反比例函数的性质进行对比)
二次函数y=ax2(a≠0)的性质
如果a>0,那么当x<0时,函数值y随着自变量x的增大而减小;当x>0时,函数值y随着自变量x的增大而增大;当x=0时,函数值最小,最小值y=0.
(师生共同完成)
如果a
<
0,那么当x<0时,函数值y随着自变量x的增大而增大;当x>0时,函数值y随着自变量x的增大而减小;当x=0时,函数值最大,最大值y=0.
(学生独立完成)
(三)例题赏析
1.
函数y=3x2
的图象的开口方向
,对称轴是
,顶点坐标为
;当x
时,函数值y随着x的增大而增大;此函数有最
值,等于
.
(讨论二次函数的图象与性质时,要从图象的开口方向,对称轴,顶点坐标,函数值的增减性以及函数的最大最小值等方面去考虑。)
2.
若函数y=(k+2)
的图象是抛物线,且当x>0时,函数y的值随x的增大而增大.
⑴求k的值;⑵求抛物线的顶点坐标和对称轴.
3.
在抛物线y=ax2(a
<
0)上有两点A(x1,y1)和B(x2,y2),若
x1>x2>0,有y1与y2的大小关系是
y1
y2.
(注意数形结合思想方法在数学学习中的应用)
4.
如图,A、B分别为抛物线y=ax2上两点,且线段AB⊥y轴于点C,若
AB=OC=6,则a的值为
.
(本题的关键是需要利用抛物线的轴对称性)
5.
记r为圆的半径,S为该圆的面积,有面积公式S=πr2,表明S是r的函数.
该函数大致图象为
(
)
注意:1.在实际问题中建立函数表达式,应注意自变量的取值范围。
2.图中横轴和纵轴相应的字母应为r和S
;图象为抛物线的一部分(原点处为空心点)
(四)自我演练
学生练习:详见随堂练习.
(五)课堂小结
1.
请你谈谈这节课的收获.
2.
揭示几种数学思想方法的应用:
⑴数形结合思想;
⑵分类讨论思想;
⑶类比思想.
(六)作业布置
1.
阅读课本第10页至第13页;
2.
课本第21页习题1、2.
C
B
A
y=-
x2
y=
x2
一、教学目标?
1.会用描点法画y=ax函数的图象.?
2.结合y=ax图象初步理解抛物线的开口方向,对称轴,顶点坐标,及二次函数的性质.?
二、教学重点、难点及教学突破?
(一)教学重点?
1.通过列表、描点、连线画函数y=ax图象.?
2.通过图象初步理解二次函数性质;
3.二次函数性质的简单应用.
(二)教学难点?
结合图象理解抛物线开口方向、对称轴、顶点坐标及基本性质,并进行归纳总结.?
(三)教学突破?
有“一次函数”画图象的基础,在画图象的基本方法上学生问题不会太大,但教师应结合列表的数据引导学生对抛物线图象大致趋势的理解.学生在结合图象观察、体会性质时会有一些困难,教师应大胆让学生自己发现,归纳,鼓励学生讨论,交流.通过学生间相互的取长补短最终能突破重难点.?
三、教学过程?
(一)复习引入?
知识回顾:
引入课题:二次函数的图象与性质(一)
(二)探索实践
在直角坐标系⑴中画出二次函数y=x2的图象
x
…
…
y=x2
…
…
图⑴
图⑵
(学生活动,注意引导学生选取合适的x的值)
强调:
1.表格中自变量x的取值应均匀,自变量x的取值的个数不宜过少,一般取5至7个值;
2.连线时应按照自变量的取值自左向右顺次连结,注意曲线要平滑,两点之间勿用线段连结,并要善于利用图形的对称性来画图。
在直角坐标系⑵中画出二次函数y=-
x2的图象
x
…
…
y=x2
…
…
学生观察图片,给出抛物线的定义:
1.
二次函数y=x2
和y=-
x2的图象是一条曲线,这样的曲线称为抛物线.
函数y=x2
的图象称为抛物线y=x2,函数y=-x2
的图象称为抛物线y=-x2.
2.
因为自变量x可以取任意实数,所以抛物线可以向上或向下无限延伸,我们所画的只是抛物线的一部分.
进一步观察图象,概括二次函数y=ax2(a≠0)图象的特点
1.
二次函数y=ax2(a≠0)的图象是一条抛物线,顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2的开口向上,在对称轴的左侧,曲线自左向右下降,在对称轴的右侧,图象自左向右上升,顶点位于抛物线的最低处;
3.当a
<0时,抛物线y=ax2的开口向下,在对称轴的左侧,曲线自左向右上升,在对称轴的右侧,图象自左向右下降,顶点位于抛物线的最高处;
(分类思想在数学学习中的应用)
根据图象的特点,分析二次函数的性质(可与一次函数和反比例函数的性质进行对比)
二次函数y=ax2(a≠0)的性质
如果a>0,那么当x<0时,函数值y随着自变量x的增大而减小;当x>0时,函数值y随着自变量x的增大而增大;当x=0时,函数值最小,最小值y=0.
(师生共同完成)
如果a
<
0,那么当x<0时,函数值y随着自变量x的增大而增大;当x>0时,函数值y随着自变量x的增大而减小;当x=0时,函数值最大,最大值y=0.
(学生独立完成)
(三)例题赏析
1.
函数y=3x2
的图象的开口方向
,对称轴是
,顶点坐标为
;当x
时,函数值y随着x的增大而增大;此函数有最
值,等于
.
(讨论二次函数的图象与性质时,要从图象的开口方向,对称轴,顶点坐标,函数值的增减性以及函数的最大最小值等方面去考虑。)
2.
若函数y=(k+2)
的图象是抛物线,且当x>0时,函数y的值随x的增大而增大.
⑴求k的值;⑵求抛物线的顶点坐标和对称轴.
3.
在抛物线y=ax2(a
<
0)上有两点A(x1,y1)和B(x2,y2),若
x1>x2>0,有y1与y2的大小关系是
y1
y2.
(注意数形结合思想方法在数学学习中的应用)
4.
如图,A、B分别为抛物线y=ax2上两点,且线段AB⊥y轴于点C,若
AB=OC=6,则a的值为
.
(本题的关键是需要利用抛物线的轴对称性)
5.
记r为圆的半径,S为该圆的面积,有面积公式S=πr2,表明S是r的函数.
该函数大致图象为
(
)
注意:1.在实际问题中建立函数表达式,应注意自变量的取值范围。
2.图中横轴和纵轴相应的字母应为r和S
;图象为抛物线的一部分(原点处为空心点)
(四)自我演练
学生练习:详见随堂练习.
(五)课堂小结
1.
请你谈谈这节课的收获.
2.
揭示几种数学思想方法的应用:
⑴数形结合思想;
⑵分类讨论思想;
⑶类比思想.
(六)作业布置
1.
阅读课本第10页至第13页;
2.
课本第21页习题1、2.
C
B
A
y=-
x2
y=
x2
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
