苏科版九下数学 5.2二次函数的图象与性质复习 教案
文档属性
| 名称 | 苏科版九下数学 5.2二次函数的图象与性质复习 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 214.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 08:00:03 | ||
图片预览

文档简介
二次函数的图象与性质复习教学设计
【教学目标】
1、会正确描述二次函数的图象,运用图象性质解决问题。
2、解决简单的数形结合问题。
【教学重点】
二次函数的图象与性质
【教学难点】
数形结合思想的运用
【教学方法】
讲练结合,分层教学
【教学过程】
教学环节
教学内容
师生活动
设计意图
一、课前小测
1、抛物线y=(x-2)2-3的开口向
;顶点坐标是
;对称轴是
;当x=
时有最
值y=
.
点A(0,y1)、B(1,y2)在该图象上,则y1
y2(填“>”、“<”或“=”)2、二次函数的图象如图所示,则下列结论正确的是(
)A.a>0,c>0
B.a>0,c<0
C.a<0,c>0
D.a<0,c<0
教师巡视,面批学生作答,5分钟完成课前小测环节。
让学生从数到形,由形到数对二次函数的性质进行回顾复习。
二、典型分析
例1:已知抛物线,请回答以下问题:抛物线的开口方向是
;抛物线的顶点坐标是________________;抛物线的的对称轴是________________;当x=
时,y有最
值为
;该抛物线与y轴的交点是
;与x轴的交点是
;选取适当的数据填入下表,并在坐标系内描点画出该抛物线的图象。x……y……
学生口答,教师提醒。小结1:二次函数的顶点式是
(a≠0)
顶点(h,k),对称轴为x=h小结2:求抛物线与坐标轴的交点:与y轴交点,令x=0;与x轴交点,令y=0
第(1)到(5)问让学生回忆二次函数图象的基本特征。第(6)问让学生掌握二次函数图象的画法。
三、分层练习
变式1:抛物线的开口方向是
;顶点坐标是
;对称轴是
;当x=
时,y有最
值为
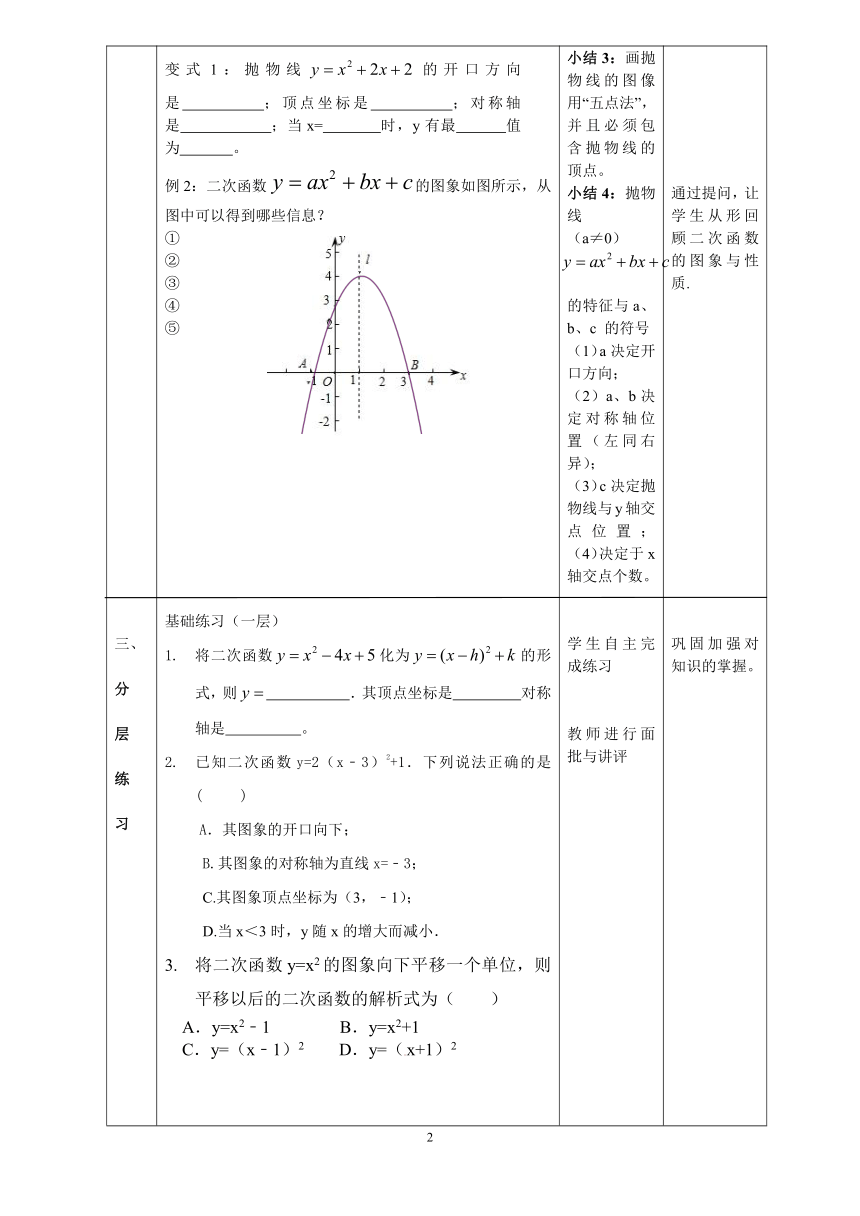
。例2:二次函数的图象如图所示,从图中可以得到哪些信息?①②③④⑤基础练习(一层)将二次函数化为的形式,则
.其顶点坐标是
对称轴是
。已知二次函数y=2(x﹣3)2+1.下列说法正确的是(
)A.其图象的开口向下;
B.其图象的对称轴为直线x=﹣3;C.其图象顶点坐标为(3,﹣1);
D.当x<3时,y随x的增大而减小.将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( ) A.y=x2﹣1
B.y=x2+1 C.y=(x﹣1)2 D.y=(x+1)2
小结3:画抛物线的图像用“五点法”,并且必须包含抛物线的顶点。小结4:抛物线
(a≠0)
的特征与a、b、c
的符号(1)a决定开口方向;(2)a、b决定对称轴位置(左同右异);(3)c决定抛物线与y轴交点位置;
(4)决定于x轴交点个数。学生自主完成练习教师进行面批与讲评
通过提问,让学生从形回顾二次函数的图象与性质.巩固加强对知识的掌握。
三、分层练习
已知抛物线的部分图象如图所示,则抛物线与x轴另外一个交点坐标是
(
)A.(2,0)
B.(3,0)
C.(4,0)
D.(5,0)已知抛物线的图象如图所示,回答下面的问题:a
0;
对称轴是
;
c=
;点A(3,y1)、B(4,y2)在这个抛物线上,则y1
y2(填“>”、“<”或“=”).
第4题图
第5题图能力训练(二层)设A,B,C是抛物线上的三点,则,,的大小关系为( )A. B. C. D.一个二次函数同时满足两个条件:①顶点是(2,1);②开口向下.这个函数解析式为
(写出一个即可)二次函数的图象如图所示,则下列关系式中错误的是(
)A.a<0
B.c>0
C.>0
D.>0
学生自主完成练习教师进行面批与讲评
分层练习,尊重学生的个体差异,满足多样化的学习需要,让不同的人在数学上得到不同的发展。
五、课后作业
拓展探索(三层)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(1,0)和(-1,2),且与y轴相交于负半轴,给出四个结论:①a<0;②b>0;③c<0;④;⑤;⑥当x>1时,y>0;⑦
a+b+c=0.其中正确结论的序号是
.(填上你认为正确结论的所有序号)抛物线的开口向
顶点坐标是
对称轴是
,当x=
时,y有最
值为
。已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是(
)A.
a>0
B.
b<0
C.
c<0
D.
a+b+c>0
课后作业,巩固该节课复习的内容。
y
x
O
1
-1
PAGE
1
【教学目标】
1、会正确描述二次函数的图象,运用图象性质解决问题。
2、解决简单的数形结合问题。
【教学重点】
二次函数的图象与性质
【教学难点】
数形结合思想的运用
【教学方法】
讲练结合,分层教学
【教学过程】
教学环节
教学内容
师生活动
设计意图
一、课前小测
1、抛物线y=(x-2)2-3的开口向
;顶点坐标是
;对称轴是
;当x=
时有最
值y=
.
点A(0,y1)、B(1,y2)在该图象上,则y1
y2(填“>”、“<”或“=”)2、二次函数的图象如图所示,则下列结论正确的是(
)A.a>0,c>0
B.a>0,c<0
C.a<0,c>0
D.a<0,c<0
教师巡视,面批学生作答,5分钟完成课前小测环节。
让学生从数到形,由形到数对二次函数的性质进行回顾复习。
二、典型分析
例1:已知抛物线,请回答以下问题:抛物线的开口方向是
;抛物线的顶点坐标是________________;抛物线的的对称轴是________________;当x=
时,y有最
值为
;该抛物线与y轴的交点是
;与x轴的交点是
;选取适当的数据填入下表,并在坐标系内描点画出该抛物线的图象。x……y……
学生口答,教师提醒。小结1:二次函数的顶点式是
(a≠0)
顶点(h,k),对称轴为x=h小结2:求抛物线与坐标轴的交点:与y轴交点,令x=0;与x轴交点,令y=0
第(1)到(5)问让学生回忆二次函数图象的基本特征。第(6)问让学生掌握二次函数图象的画法。
三、分层练习
变式1:抛物线的开口方向是
;顶点坐标是
;对称轴是
;当x=
时,y有最
值为
。例2:二次函数的图象如图所示,从图中可以得到哪些信息?①②③④⑤基础练习(一层)将二次函数化为的形式,则
.其顶点坐标是
对称轴是
。已知二次函数y=2(x﹣3)2+1.下列说法正确的是(
)A.其图象的开口向下;
B.其图象的对称轴为直线x=﹣3;C.其图象顶点坐标为(3,﹣1);
D.当x<3时,y随x的增大而减小.将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( ) A.y=x2﹣1
B.y=x2+1 C.y=(x﹣1)2 D.y=(x+1)2
小结3:画抛物线的图像用“五点法”,并且必须包含抛物线的顶点。小结4:抛物线
(a≠0)
的特征与a、b、c
的符号(1)a决定开口方向;(2)a、b决定对称轴位置(左同右异);(3)c决定抛物线与y轴交点位置;
(4)决定于x轴交点个数。学生自主完成练习教师进行面批与讲评
通过提问,让学生从形回顾二次函数的图象与性质.巩固加强对知识的掌握。
三、分层练习
已知抛物线的部分图象如图所示,则抛物线与x轴另外一个交点坐标是
(
)A.(2,0)
B.(3,0)
C.(4,0)
D.(5,0)已知抛物线的图象如图所示,回答下面的问题:a
0;
对称轴是
;
c=
;点A(3,y1)、B(4,y2)在这个抛物线上,则y1
y2(填“>”、“<”或“=”).
第4题图
第5题图能力训练(二层)设A,B,C是抛物线上的三点,则,,的大小关系为( )A. B. C. D.一个二次函数同时满足两个条件:①顶点是(2,1);②开口向下.这个函数解析式为
(写出一个即可)二次函数的图象如图所示,则下列关系式中错误的是(
)A.a<0
B.c>0
C.>0
D.>0
学生自主完成练习教师进行面批与讲评
分层练习,尊重学生的个体差异,满足多样化的学习需要,让不同的人在数学上得到不同的发展。
五、课后作业
拓展探索(三层)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(1,0)和(-1,2),且与y轴相交于负半轴,给出四个结论:①a<0;②b>0;③c<0;④;⑤;⑥当x>1时,y>0;⑦
a+b+c=0.其中正确结论的序号是
.(填上你认为正确结论的所有序号)抛物线的开口向
顶点坐标是
对称轴是
,当x=
时,y有最
值为
。已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是(
)A.
a>0
B.
b<0
C.
c<0
D.
a+b+c>0
课后作业,巩固该节课复习的内容。
y
x
O
1
-1
PAGE
1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
