人教版数学五年级下册:9 总复习 课件(共52张PPT)
文档属性
| 名称 | 人教版数学五年级下册:9 总复习 课件(共52张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 15:41:10 | ||
图片预览










文档简介
(共52张PPT)
总复习
因数和倍数
偶
数
奇
数
5的倍数的特征
3的倍数的特征
2的倍数的特征
最小公倍数
公倍数
倍
数
最大公因数
质
数
合
数
公因数
因
数
一、知识梳理
“因数和倍数”这部分内容最基本的概念是什么?你能从基本概念出发,把有关联的知识整理成一个图吗?
二、概念复习
(一)因数和倍数
填一填:
(1)15的因数有(
)。
(2)3的倍数有(
)。
1、3、5、15
3、6、9、12、15
……
(二)2、5、3的倍数的特征
56、79、87、195、204、630、22、31、57、65、78、83
下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
个位上是0,2,4,6,8的数都是2的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
偶数有:56、204、630、22、78
奇数有:79、87、195、31、57、65、83
2的倍数有:56、204、630、22、78
3的倍数有:87、195、204、630、57、78
5的倍数有:195、630、65
个位上是0或5的数都是5的倍数。
整数中,不是2的倍数的数叫做奇数。
整数中,是2的倍数的数叫做偶数(0也是偶数)。
二、概念复习
(三)质数和合数
56、79、87、195、204、630、22、31、57、65、78、83
下面的数,哪些是质数?哪些是合数?说一说你是怎样判断的。
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
1不是质数,也不是合数。
质数有:79、31、83
合数有:56、87、195、204、630、22、57、65、78
二、概念复习
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
(三)质数和合数
填一填:
(1)奇数+偶数=(
)
(2)奇数+奇数=(
)
(3)偶数+偶数=(
)
(4)奇数×偶数=(
)
(5)奇数×奇数=(
)
(6)偶数×偶数=(
)
奇数
偶数
偶数
奇数
偶数
100以内的质数有哪些?
偶数
二、概念复习
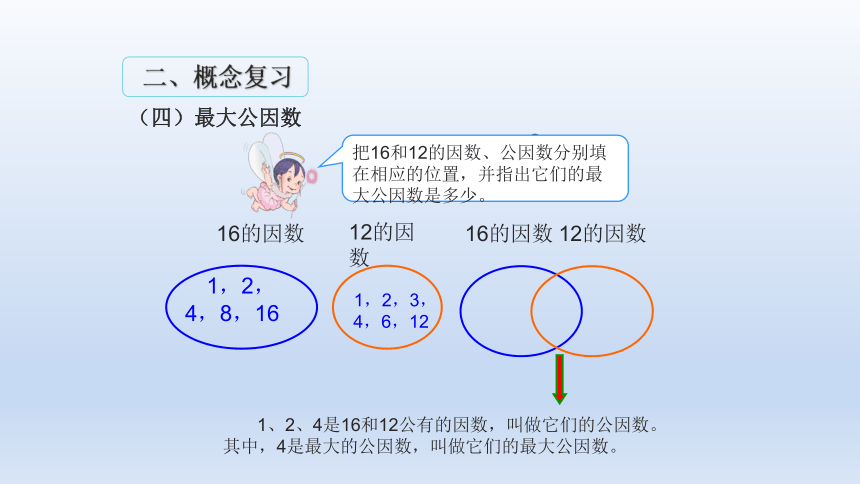
(四)最大公因数
16的因数
12的因数
1,2,3,4,6,12
1,2,4,8,16
16的因数
12的因数
16
6
12
3
8
1
2
4
1、2、4是16和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数,叫做它们的最大公因数。
把16和12的因数、公因数分别填在相应的位置,并指出它们的最大公因数是多少。
二、概念复习
(四)最大公因数
4
和
8
12
和
36
1
和
7
8
和
9
12
和
35
找出下列每组数的最大公因数。
做完后你发现了什么?
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1
时,它们的最大公因数也是1。
两个数的公因数和它们的最大公因数之间有什么关系?
所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
二、概念复习
3的倍数
2的倍数
3,
9,15,
21···
2,
4,
8,
10,
14,
16,
20
···
6,12,
18,···
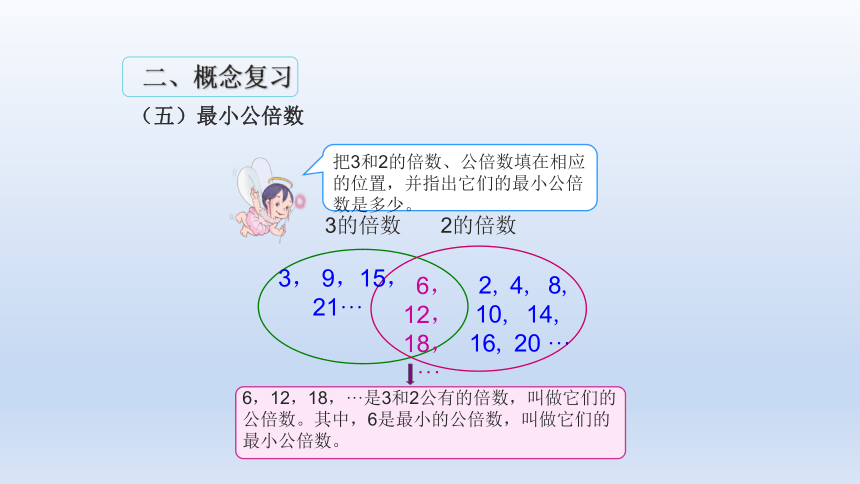
把3和2的倍数、公倍数填在相应的位置,并指出它们的最小公倍数是多少。
6,12,18,···是3和2公有的倍数,叫做它们的公倍数。其中,6是最小的公倍数,叫做它们的最小公倍数。
(五)最小公倍数
二、概念复习
(五)最小公倍数
4
和
8
12
和
36
1
和
7
8
和
9
5
和
10
找出下列每组数的最小公倍数。
做完后你发现了什么?
当两个数成倍数关系时,较大的数就是它们的最小公倍数。
如果两个数的最大公因数是1
,那么这两个数的积就是它们的最小公倍数。
两个数的公倍数和它们的最小公倍数之间有什么关系?
两个数的公倍数都是最小公倍数的倍数。
二、概念复习
食品店有70多个松花蛋,如果把它装进4个一排的蛋托中,正好装完。如果把它装进6个一排的蛋托中,也正好装完。你能求出有多少个松花蛋吗?
把这些松花蛋如果装进4个一排的蛋托中,正好装完。如果装进6个一排的蛋托中,也正好装完。说明这些松花蛋是4和6的公倍数。我们可以先求出4和6的最小公倍数是12,因为食品店有70多个松花蛋,所以用12×6=72求出有72个松花蛋。
这个问题该怎样思考呢?
三、解决问题
分数的意义和性质
分数的加法和减法
一、分数的意义和性质
分数和小数的互化
真分数
分数的种类
假分数
带份数或整数
分数的基本性质
约分
通分
通分及其方法
比较分数的大小
约分及其方法
最简分数
求一个数是另一个数的几分之几
分数的意义和性质
分数的意义
分数的产生
分数的意义
分数与除法
单位“1”
分数单位
化成
一个物体、一个计量单位或是一些物体等都可以看作一个整体。把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
一个整体可以用自然数1来表示,我们通常把它叫做单位“1”。
把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
在进行测量、分物或计算时,往往不能正好得到整数的结果,这时常用什么数来表示?
常用分数来表示。
一、分数的意义和性质
(2)1985年,第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查的野生大熊猫的数量是第三次调查数量的(
),生活在四川的野生大熊猫占第三次调查的野生大熊猫数量的(
)。
填一填:
(1)把4m长的绳子平均剪成5段,每段长(
)m,每段绳子是全长的(
)。
4
5
1
5
201
266
557
798
一、分数的意义和性质
如果用字母a表示被除数,b表示除数。
a÷b=
(b≠0)
3
4
3÷4=
用字母表示分数与除法的关系:
1
3
1÷3=
被除数÷除数=
被除数
除数
b可以是0吗?
我们一起来回忆:分数与除法有什么关系?
b
a
一、分数的意义和性质
3
13
4
13
<
比较下列分数的大小,并说出你的理由。
3
8
3
11
>
2
7
4
7
5
6
5
8
5
9
2
9
12
17
12
19
<
>
>
>
分母相同
分子相同
的两个分数,分子大的分数就大。
的两个分数,分母小的分数就大。
大家说一说:分母相同的两个分数怎样比较大小?分子相同的两个分数呢?
一、分数的意义和性质
3
4
5
6
<
可以先通分,把它们化成分母相同的分数。
6
5
=
6×2
5×2
=
10
12
=
4
3
=
4×3
3×3
=
9
12
=
因为
9
12
<
10
12
,所以
3
4
<
5
6
大家说一说:分子和分母都不相同的两个分数怎么比较大小?
一、分数的意义和性质
0.125
3
10
0.5
1
4
0
1
0.25
0.3
0.8
1
8
1
2
5
8
3
4
0.75
4
5
在
里填上适当的小数或分数。
0.625
一、分数的意义和性质
用小数表示
用分数表示
40cm
150g
125cm2
3680dm3
m
m
kg
kg
dm2
dm2
m3
m3
0.4
0.15
1.25
3.68
在下表的空格里填上适当的数,使每行的3个数量都相等。
2
5
1
4
1
3
20
17
25
3
一、分数的意义和性质
二、分数的加法和减法
14
5
7
4
=
+
14
3
3
1
12
7
7
4
7
3
+
=
1
9
4
9
7
-
=
4
1
3
1
+
=
3
2
6
5
-
=
6
1
5
1
4
1
-
=
20
1
同分母分数相加、减,分母不变,只把分子相加减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果,能约分的要约成最简分数。
计算下面各题
计算时应注意什么?
2
-
12
3
12
+
6
12
=
2
12
-
9
12
=
7
12
=
2
1
+
6
5
-
(
)
3
1
6
1
4
1
-
2
1
+
5
6
=
-
6
5
0
=
-
(
)
5
6
=
+
6
3
6
2
分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同。
没有括号的分数加减混合运算要从左往右依次进行。
有括号的分数加减混合运算要先算括号里面的,后算括号外面的。
计算下面各题。
大家来回忆一下分数加减混合运算的运算顺序。
二、分数的加法和减法
图形与几何
从上面看
从正面看
从左面看
根据下面从不同方向看到的图形摆一摆。
一、观察物体(三)
(一)长方体、正方体的异同
长方体和正方体有哪些相同点?有哪些不同点?
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点。
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
二、长方体和正方体
1.
长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
(二)长方体、正方体表面积的含义
二、长方体和正方体
(1)正方形棱长与每个面边长的关系
2.正方体表面积的含义
(二)长方体、正方体表面积的含义
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
二、长方体和正方体
(2)正方形的11种展开图。
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第一类:中间四连方,两侧各有一个,共6种。
图(1)
图(2)
图(3)
图(6)
图(5)
图(4)
二、长方体和正方体
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第二类:中间三连方,一侧有一个、一侧有二个,共3种。
图(8)
图(9)
图(7)
(2)正方形的11种展开图。
二、长方体和正方体
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第三类:中间两连方,两侧各有2个、只有1种。
第四类:两排各有3个、只有1种。
图(1)
(2)正方形的11种展开图。
图(11)
二、长方体和正方体
(三)长方体、正方体体积公式的推导
底面积
长方体(或正方体)的
体积
=
底面积×高
长方体的体积
=
长×宽×高
底面积
正方体的体积
=
棱长×棱长×棱长
可看作是高
二、长方体和正方体
名
称
图形及条件
表
面
积
体
积
长方体
S=
V=
正方体
S
=
V
=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
填写下表。
二、长方体和正方体
(四)体积与容积的区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和mL;计量固体时用体积单位。
联系
1.容积的大小是通过所能容纳物体的体积表示出来的。
2.计算方法相同。
二、长方体和正方体
逆
三、图形的运动(三)
风车绕点O(
)
时针旋转。
风车绕点O
(
)
时针旋转。
逆
90
90
描述旋转时要说清所绕的点、旋转的方向和角度。
画出绕点
O,顺时针旋转90
后的图形。
A
O
B
三、图形的运动(三)
A
O
B
A'
A
O
B
A'
A
O
B
A'
B'
A
O
B
A'
B'
(图一)三角形绕点O(
)时针旋转了(
)度。
(图二)三角形绕点O(
)时针旋转了(
)度。
逆
90
顺
90
旋转不改变图形的形状、大小,只改变图形的位置。
图(一)
图(二)
三、图形的运动(三)
有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是(
)
cm?。
18cm
18cm
18cm
364.5
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
根据题意,我们先来画画图。
四、知识应用
折线统计图
一、知识回顾
观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
折线统计图适合表示数据的增减变化情况。
单式折线统计图只能看出一组数据变化的整体趋势,而复式折线统计图可以比较方便地比较两组数据的变化趋势。
复式折线统计图与单式折线统计图有什么不同?
一、知识回顾
也可以用实线和虚线进行区分。
还得用图例说明两种颜色折线分别代表什么?
要画两条折线,并且要用颜色区分开。
说一说绘制复式折线统计图时应该注意什么?
一、知识回顾
二、数据分析
从统计图中可以看出某大学理工科在河北省招生的分数较高,基本都在600分以上,尤其是近四年的分数都在630分左右,估计今年的分数也会较高。我如果想上这所大学的理工科的话,需要加倍努力!
如果你是高考生,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
如果你是商场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
通过对比两条折线的走势,我分析出:A牌彩电销售量逐渐降低,而B牌彩电的销售量在逐步提高并超过了A牌彩电的销量。如果我是商场经理,可以根据这种变化趋势做出决策,加大B牌彩电的进货量,同时降低A牌彩电的进货量,以保证比较稳定的销售额。
二、数据分析
三、解决问题
2000年学龄儿童最多,2010年学龄儿童最少。
根据这幅统计图,你能提出什么数学问题?
哪年学龄儿童最多?哪年最少?
2002年没上学的学龄儿童最多,2010年没上学的学龄儿童最少。
根据这幅统计图,你能提出什么数学问题?
你还能发现什么?
哪年没上学的学龄儿童最多?哪年最少?
三、解决问题
在复式折线统计图中,既可以看出每组数据变化的整体趋势,还能对两组数据的差异进行分析、比较,并通过所获得的信息对事物的发展趋势进行推测。
复式折线统计图有什么优点?
三、解决问题
谢
谢
总复习
因数和倍数
偶
数
奇
数
5的倍数的特征
3的倍数的特征
2的倍数的特征
最小公倍数
公倍数
倍
数
最大公因数
质
数
合
数
公因数
因
数
一、知识梳理
“因数和倍数”这部分内容最基本的概念是什么?你能从基本概念出发,把有关联的知识整理成一个图吗?
二、概念复习
(一)因数和倍数
填一填:
(1)15的因数有(
)。
(2)3的倍数有(
)。
1、3、5、15
3、6、9、12、15
……
(二)2、5、3的倍数的特征
56、79、87、195、204、630、22、31、57、65、78、83
下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
个位上是0,2,4,6,8的数都是2的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
偶数有:56、204、630、22、78
奇数有:79、87、195、31、57、65、83
2的倍数有:56、204、630、22、78
3的倍数有:87、195、204、630、57、78
5的倍数有:195、630、65
个位上是0或5的数都是5的倍数。
整数中,不是2的倍数的数叫做奇数。
整数中,是2的倍数的数叫做偶数(0也是偶数)。
二、概念复习
(三)质数和合数
56、79、87、195、204、630、22、31、57、65、78、83
下面的数,哪些是质数?哪些是合数?说一说你是怎样判断的。
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
1不是质数,也不是合数。
质数有:79、31、83
合数有:56、87、195、204、630、22、57、65、78
二、概念复习
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
(三)质数和合数
填一填:
(1)奇数+偶数=(
)
(2)奇数+奇数=(
)
(3)偶数+偶数=(
)
(4)奇数×偶数=(
)
(5)奇数×奇数=(
)
(6)偶数×偶数=(
)
奇数
偶数
偶数
奇数
偶数
100以内的质数有哪些?
偶数
二、概念复习
(四)最大公因数
16的因数
12的因数
1,2,3,4,6,12
1,2,4,8,16
16的因数
12的因数
16
6
12
3
8
1
2
4
1、2、4是16和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数,叫做它们的最大公因数。
把16和12的因数、公因数分别填在相应的位置,并指出它们的最大公因数是多少。
二、概念复习
(四)最大公因数
4
和
8
12
和
36
1
和
7
8
和
9
12
和
35
找出下列每组数的最大公因数。
做完后你发现了什么?
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1
时,它们的最大公因数也是1。
两个数的公因数和它们的最大公因数之间有什么关系?
所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
二、概念复习
3的倍数
2的倍数
3,
9,15,
21···
2,
4,
8,
10,
14,
16,
20
···
6,12,
18,···
把3和2的倍数、公倍数填在相应的位置,并指出它们的最小公倍数是多少。
6,12,18,···是3和2公有的倍数,叫做它们的公倍数。其中,6是最小的公倍数,叫做它们的最小公倍数。
(五)最小公倍数
二、概念复习
(五)最小公倍数
4
和
8
12
和
36
1
和
7
8
和
9
5
和
10
找出下列每组数的最小公倍数。
做完后你发现了什么?
当两个数成倍数关系时,较大的数就是它们的最小公倍数。
如果两个数的最大公因数是1
,那么这两个数的积就是它们的最小公倍数。
两个数的公倍数和它们的最小公倍数之间有什么关系?
两个数的公倍数都是最小公倍数的倍数。
二、概念复习
食品店有70多个松花蛋,如果把它装进4个一排的蛋托中,正好装完。如果把它装进6个一排的蛋托中,也正好装完。你能求出有多少个松花蛋吗?
把这些松花蛋如果装进4个一排的蛋托中,正好装完。如果装进6个一排的蛋托中,也正好装完。说明这些松花蛋是4和6的公倍数。我们可以先求出4和6的最小公倍数是12,因为食品店有70多个松花蛋,所以用12×6=72求出有72个松花蛋。
这个问题该怎样思考呢?
三、解决问题
分数的意义和性质
分数的加法和减法
一、分数的意义和性质
分数和小数的互化
真分数
分数的种类
假分数
带份数或整数
分数的基本性质
约分
通分
通分及其方法
比较分数的大小
约分及其方法
最简分数
求一个数是另一个数的几分之几
分数的意义和性质
分数的意义
分数的产生
分数的意义
分数与除法
单位“1”
分数单位
化成
一个物体、一个计量单位或是一些物体等都可以看作一个整体。把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
一个整体可以用自然数1来表示,我们通常把它叫做单位“1”。
把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
在进行测量、分物或计算时,往往不能正好得到整数的结果,这时常用什么数来表示?
常用分数来表示。
一、分数的意义和性质
(2)1985年,第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查的野生大熊猫的数量是第三次调查数量的(
),生活在四川的野生大熊猫占第三次调查的野生大熊猫数量的(
)。
填一填:
(1)把4m长的绳子平均剪成5段,每段长(
)m,每段绳子是全长的(
)。
4
5
1
5
201
266
557
798
一、分数的意义和性质
如果用字母a表示被除数,b表示除数。
a÷b=
(b≠0)
3
4
3÷4=
用字母表示分数与除法的关系:
1
3
1÷3=
被除数÷除数=
被除数
除数
b可以是0吗?
我们一起来回忆:分数与除法有什么关系?
b
a
一、分数的意义和性质
3
13
4
13
<
比较下列分数的大小,并说出你的理由。
3
8
3
11
>
2
7
4
7
5
6
5
8
5
9
2
9
12
17
12
19
<
>
>
>
分母相同
分子相同
的两个分数,分子大的分数就大。
的两个分数,分母小的分数就大。
大家说一说:分母相同的两个分数怎样比较大小?分子相同的两个分数呢?
一、分数的意义和性质
3
4
5
6
<
可以先通分,把它们化成分母相同的分数。
6
5
=
6×2
5×2
=
10
12
=
4
3
=
4×3
3×3
=
9
12
=
因为
9
12
<
10
12
,所以
3
4
<
5
6
大家说一说:分子和分母都不相同的两个分数怎么比较大小?
一、分数的意义和性质
0.125
3
10
0.5
1
4
0
1
0.25
0.3
0.8
1
8
1
2
5
8
3
4
0.75
4
5
在
里填上适当的小数或分数。
0.625
一、分数的意义和性质
用小数表示
用分数表示
40cm
150g
125cm2
3680dm3
m
m
kg
kg
dm2
dm2
m3
m3
0.4
0.15
1.25
3.68
在下表的空格里填上适当的数,使每行的3个数量都相等。
2
5
1
4
1
3
20
17
25
3
一、分数的意义和性质
二、分数的加法和减法
14
5
7
4
=
+
14
3
3
1
12
7
7
4
7
3
+
=
1
9
4
9
7
-
=
4
1
3
1
+
=
3
2
6
5
-
=
6
1
5
1
4
1
-
=
20
1
同分母分数相加、减,分母不变,只把分子相加减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果,能约分的要约成最简分数。
计算下面各题
计算时应注意什么?
2
-
12
3
12
+
6
12
=
2
12
-
9
12
=
7
12
=
2
1
+
6
5
-
(
)
3
1
6
1
4
1
-
2
1
+
5
6
=
-
6
5
0
=
-
(
)
5
6
=
+
6
3
6
2
分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同。
没有括号的分数加减混合运算要从左往右依次进行。
有括号的分数加减混合运算要先算括号里面的,后算括号外面的。
计算下面各题。
大家来回忆一下分数加减混合运算的运算顺序。
二、分数的加法和减法
图形与几何
从上面看
从正面看
从左面看
根据下面从不同方向看到的图形摆一摆。
一、观察物体(三)
(一)长方体、正方体的异同
长方体和正方体有哪些相同点?有哪些不同点?
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点。
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
二、长方体和正方体
1.
长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
(二)长方体、正方体表面积的含义
二、长方体和正方体
(1)正方形棱长与每个面边长的关系
2.正方体表面积的含义
(二)长方体、正方体表面积的含义
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
二、长方体和正方体
(2)正方形的11种展开图。
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第一类:中间四连方,两侧各有一个,共6种。
图(1)
图(2)
图(3)
图(6)
图(5)
图(4)
二、长方体和正方体
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第二类:中间三连方,一侧有一个、一侧有二个,共3种。
图(8)
图(9)
图(7)
(2)正方形的11种展开图。
二、长方体和正方体
(二)长方体、正方体表面积的含义
2.正方体表面积的含义
第三类:中间两连方,两侧各有2个、只有1种。
第四类:两排各有3个、只有1种。
图(1)
(2)正方形的11种展开图。
图(11)
二、长方体和正方体
(三)长方体、正方体体积公式的推导
底面积
长方体(或正方体)的
体积
=
底面积×高
长方体的体积
=
长×宽×高
底面积
正方体的体积
=
棱长×棱长×棱长
可看作是高
二、长方体和正方体
名
称
图形及条件
表
面
积
体
积
长方体
S=
V=
正方体
S
=
V
=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
填写下表。
二、长方体和正方体
(四)体积与容积的区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和mL;计量固体时用体积单位。
联系
1.容积的大小是通过所能容纳物体的体积表示出来的。
2.计算方法相同。
二、长方体和正方体
逆
三、图形的运动(三)
风车绕点O(
)
时针旋转。
风车绕点O
(
)
时针旋转。
逆
90
90
描述旋转时要说清所绕的点、旋转的方向和角度。
画出绕点
O,顺时针旋转90
后的图形。
A
O
B
三、图形的运动(三)
A
O
B
A'
A
O
B
A'
A
O
B
A'
B'
A
O
B
A'
B'
(图一)三角形绕点O(
)时针旋转了(
)度。
(图二)三角形绕点O(
)时针旋转了(
)度。
逆
90
顺
90
旋转不改变图形的形状、大小,只改变图形的位置。
图(一)
图(二)
三、图形的运动(三)
有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是(
)
cm?。
18cm
18cm
18cm
364.5
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
根据题意,我们先来画画图。
四、知识应用
折线统计图
一、知识回顾
观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
折线统计图适合表示数据的增减变化情况。
单式折线统计图只能看出一组数据变化的整体趋势,而复式折线统计图可以比较方便地比较两组数据的变化趋势。
复式折线统计图与单式折线统计图有什么不同?
一、知识回顾
也可以用实线和虚线进行区分。
还得用图例说明两种颜色折线分别代表什么?
要画两条折线,并且要用颜色区分开。
说一说绘制复式折线统计图时应该注意什么?
一、知识回顾
二、数据分析
从统计图中可以看出某大学理工科在河北省招生的分数较高,基本都在600分以上,尤其是近四年的分数都在630分左右,估计今年的分数也会较高。我如果想上这所大学的理工科的话,需要加倍努力!
如果你是高考生,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
如果你是商场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
通过对比两条折线的走势,我分析出:A牌彩电销售量逐渐降低,而B牌彩电的销售量在逐步提高并超过了A牌彩电的销量。如果我是商场经理,可以根据这种变化趋势做出决策,加大B牌彩电的进货量,同时降低A牌彩电的进货量,以保证比较稳定的销售额。
二、数据分析
三、解决问题
2000年学龄儿童最多,2010年学龄儿童最少。
根据这幅统计图,你能提出什么数学问题?
哪年学龄儿童最多?哪年最少?
2002年没上学的学龄儿童最多,2010年没上学的学龄儿童最少。
根据这幅统计图,你能提出什么数学问题?
你还能发现什么?
哪年没上学的学龄儿童最多?哪年最少?
三、解决问题
在复式折线统计图中,既可以看出每组数据变化的整体趋势,还能对两组数据的差异进行分析、比较,并通过所获得的信息对事物的发展趋势进行推测。
复式折线统计图有什么优点?
三、解决问题
谢
谢
