竖直平面内的圆周运动
图片预览




文档简介
(共13张PPT)
竖直平面内的圆周运动
【回顾】研究圆周运动的思路
从“供”“需”两方面来进行研究:
1、“供”——分析物体受力,求沿半径方 向的合外力;
2、“需”——确定物体轨道,定圆心、找 半径、用公式,求出所需向心力;
3、“供”“需”平衡则做圆周运动。
应用Fn=man列方程并求解。
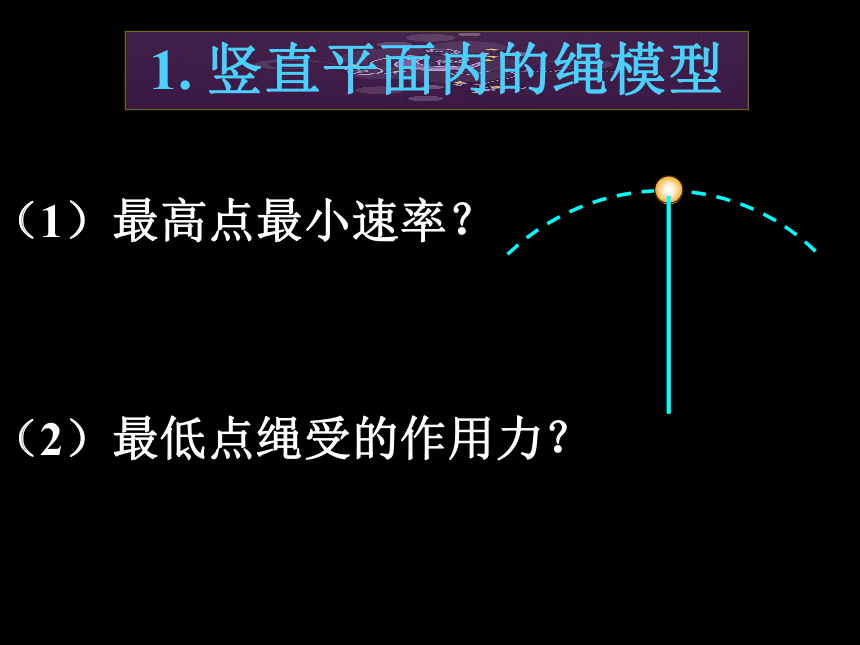
1. 竖直平面内的绳模型
(1)最高点最小速率?
(2)最低点绳受的作用力?
1. 水不流出的最小速率?
2. 在最低点水对碗的压力?
拓展:水流星问题
拓展2:外轨道问题
1. 水不流出的最小速率?
2. 在最低点水对碗的压力?
拓展1:水流星问题
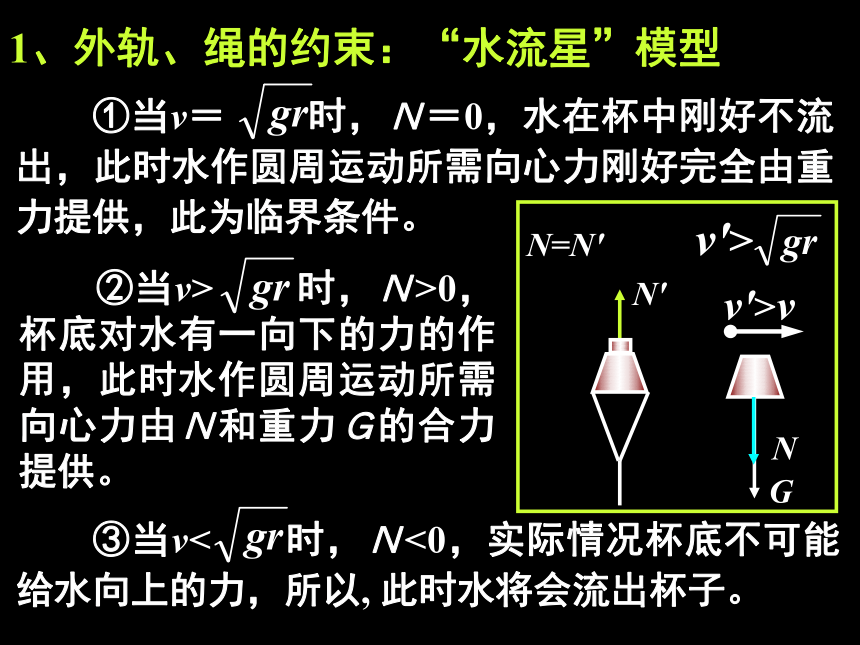
1、外轨、绳的约束:“水流星”模型
②当v> 时,N>0,杯底对水有一向下的力的作用,此时水作圆周运动所需向心力由N和重力G的合力提供。
①当v= 时,N=0,水在杯中刚好不流出,此时水作圆周运动所需向心力刚好完全由重力提供,此为临界条件。
③当v< 时,N<0,实际情况杯底不可能给水向上的力,所以, 此时水将会流出杯子。
v'>
v'>v
N=N'
N'
N
G
1. 最高点速率问题?
2. 在最低点杆的受力问题?
3. 在最高点杆的受力问题?
2. 竖直平面内杆的问题
拓展1:内轨道问题
(1) 最小速率?
(2) 立即离开球顶的最小速率?落 在什么位置?半径为R
(1)最高点最小速率?
(2)最高点和最低点的受力问题?
拓展2:管道问题
3、内外轨同时约束、杆约束
②当v > 时, 压外轨,且v越大压力 越大(杆对小球提供拉力)
①当v= 时,N=0
③当v < 时, 压内轨,且v越小压力 越大(杆对小球提供支持力)
【P31T3】如图, 细绳一端 系着质量为m的物体A,另一端 通过光滑小孔O吊着质量m的 物体B, A的中点与圆孔的距离为r, 并已知A与水平面间的动摩擦因数为μ, 现使此平面绕中心轴线转动, 问角速度 在什么范围内, A可处于相对桌面静止状态 (g=10m/s2)
题型一 有关摩擦力的临界问题
B
O
A
【P33例3】如图, 两绳系一个 质量为m=0.1kg的小球, 两绳 的另两端分别固定于轴上的 A、B两处, 上面绳长l=2m, 两 绳都拉直时与轴夹角分别为 30 与45 , 问球的角速度在什么范围内, 两绳始终张紧 (g取10m/s2)
题型二 水平面内圆周运动的临界问题
l
A
B
2.40rad/s< <3.16rad/s
3、圆周运动的临界问题分析
找圆周运动的临界状态时,可假设V或ω逐渐增大,由圆周运动规律判断增大过程中会出现何种恰好怎样的状态,即为临界状态
竖直平面内的圆周运动
【回顾】研究圆周运动的思路
从“供”“需”两方面来进行研究:
1、“供”——分析物体受力,求沿半径方 向的合外力;
2、“需”——确定物体轨道,定圆心、找 半径、用公式,求出所需向心力;
3、“供”“需”平衡则做圆周运动。
应用Fn=man列方程并求解。
1. 竖直平面内的绳模型
(1)最高点最小速率?
(2)最低点绳受的作用力?
1. 水不流出的最小速率?
2. 在最低点水对碗的压力?
拓展:水流星问题
拓展2:外轨道问题
1. 水不流出的最小速率?
2. 在最低点水对碗的压力?
拓展1:水流星问题
1、外轨、绳的约束:“水流星”模型
②当v> 时,N>0,杯底对水有一向下的力的作用,此时水作圆周运动所需向心力由N和重力G的合力提供。
①当v= 时,N=0,水在杯中刚好不流出,此时水作圆周运动所需向心力刚好完全由重力提供,此为临界条件。
③当v< 时,N<0,实际情况杯底不可能给水向上的力,所以, 此时水将会流出杯子。
v'>
v'>v
N=N'
N'
N
G
1. 最高点速率问题?
2. 在最低点杆的受力问题?
3. 在最高点杆的受力问题?
2. 竖直平面内杆的问题
拓展1:内轨道问题
(1) 最小速率?
(2) 立即离开球顶的最小速率?落 在什么位置?半径为R
(1)最高点最小速率?
(2)最高点和最低点的受力问题?
拓展2:管道问题
3、内外轨同时约束、杆约束
②当v > 时, 压外轨,且v越大压力 越大(杆对小球提供拉力)
①当v= 时,N=0
③当v < 时, 压内轨,且v越小压力 越大(杆对小球提供支持力)
【P31T3】如图, 细绳一端 系着质量为m的物体A,另一端 通过光滑小孔O吊着质量m的 物体B, A的中点与圆孔的距离为r, 并已知A与水平面间的动摩擦因数为μ, 现使此平面绕中心轴线转动, 问角速度 在什么范围内, A可处于相对桌面静止状态 (g=10m/s2)
题型一 有关摩擦力的临界问题
B
O
A
【P33例3】如图, 两绳系一个 质量为m=0.1kg的小球, 两绳 的另两端分别固定于轴上的 A、B两处, 上面绳长l=2m, 两 绳都拉直时与轴夹角分别为 30 与45 , 问球的角速度在什么范围内, 两绳始终张紧 (g取10m/s2)
题型二 水平面内圆周运动的临界问题
l
A
B
2.40rad/s< <3.16rad/s
3、圆周运动的临界问题分析
找圆周运动的临界状态时,可假设V或ω逐渐增大,由圆周运动规律判断增大过程中会出现何种恰好怎样的状态,即为临界状态
