向量的加法
图片预览










文档简介
(共67张PPT)
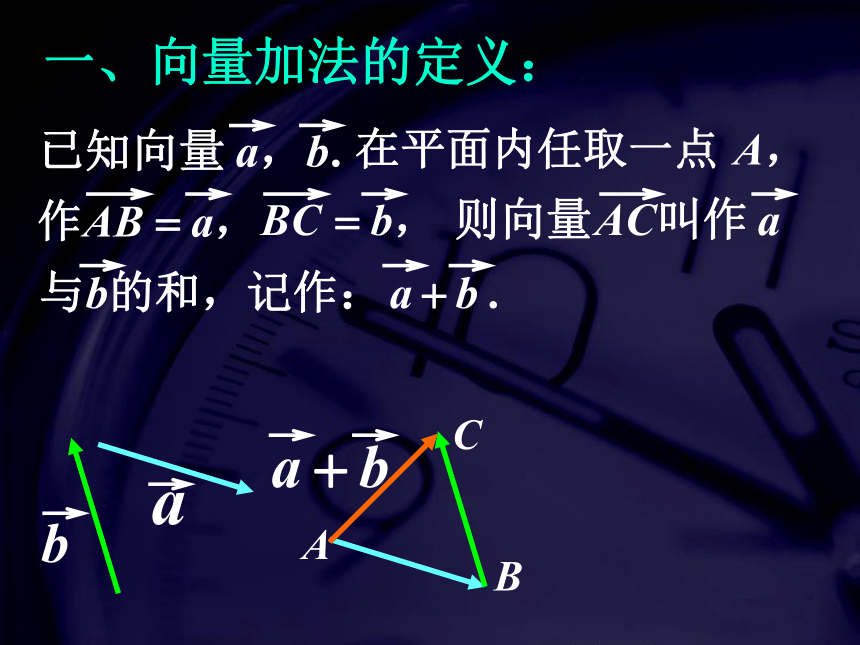
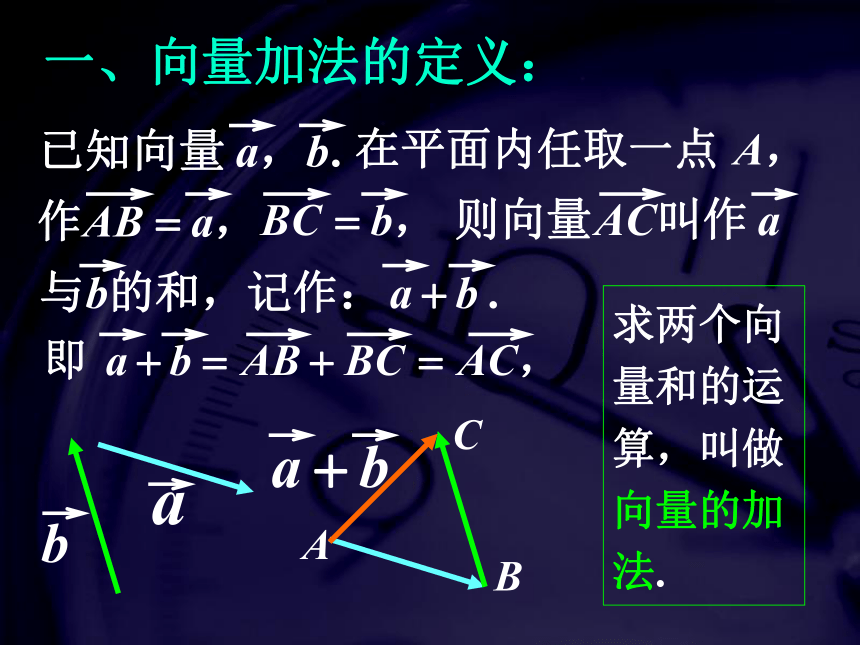
一、向量加法的定义:
一、向量加法的定义:
一、向量加法的定义:
A
一、向量加法的定义:
A
B
一、向量加法的定义:
A
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
求两个向 量和的运 算,叫做 向量的加 法.
一、向量加法的定义:
A
C
B
求两个向 量和的运 算,叫做 向量的加 法.
一、向量加法的定义:
二、向量加法的三角形法则:
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
特点: 首 尾 相 接
第二个向量要以第一个向量的终点
为起点,则由第一个向量的起点指向第
二个向量的终点的向量为和向量.
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
特点: 首 尾 相 接
例1
O
例1
O
A
例1
O
A
B
例1
O
A
B
例1
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
将n个向量首尾相接,以第一个向量的起点为起点,最后一个向量的终点为终点的向量,即为这n个向量的和向量。
将n个向量首尾相接,以第一个向量的起点为起点,最后一个向量的终点为终点的向量,即为这n个向量的和向量。
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
思考: 向量的加法满足交换律和结合律吗
A
B
C
思考: 向量的加法满足交换律和结合律吗
A
B
C
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
三、向量加法的平行四边形法则:
作两个向量的和的方法
叫做向量加法的平行四
边形法则.
A
B
C
D
三、向量加法的平行四边形法则:
km/h的速度向垂直于对岸的方向行驶,同时河水的流速为
2km/h,求船实际航 行速度的大小与方 向.
A
D
C
B
例2
方法小结:
方法小结:
三角形法则适用于首尾相接的向量求和;而平行四边形法则适用于同起点的两个向量求和;但共线向量求和时,则三角形法则较合适.
例3:下列各式的结果为零向量
的有( )个
例4:利用向量的对角线
思 考:
一、向量加法的定义:
一、向量加法的定义:
一、向量加法的定义:
A
一、向量加法的定义:
A
B
一、向量加法的定义:
A
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
一、向量加法的定义:
A
C
B
求两个向 量和的运 算,叫做 向量的加 法.
一、向量加法的定义:
A
C
B
求两个向 量和的运 算,叫做 向量的加 法.
一、向量加法的定义:
二、向量加法的三角形法则:
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
特点: 首 尾 相 接
第二个向量要以第一个向量的终点
为起点,则由第一个向量的起点指向第
二个向量的终点的向量为和向量.
二、向量加法的三角形法则:
根据向量加法的定义得出的求向量
和的方法,称为向量加法的三角形法则.
特点: 首 尾 相 接
例1
O
例1
O
A
例1
O
A
B
例1
O
A
B
例1
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
将n个向量首尾相接,以第一个向量的起点为起点,最后一个向量的终点为终点的向量,即为这n个向量的和向量。
将n个向量首尾相接,以第一个向量的起点为起点,最后一个向量的终点为终点的向量,即为这n个向量的和向量。
A
B
C
D
E
F
K
J
如果三个向量相加,四个向量相加,…n 个向量相加,和向量又如何?
思考: 向量的加法满足交换律和结合律吗
A
B
C
思考: 向量的加法满足交换律和结合律吗
A
B
C
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
A
D
B
C
A
B
C
D
思考: 向量的加法满足交换律和结合律吗
三、向量加法的平行四边形法则:
作两个向量的和的方法
叫做向量加法的平行四
边形法则.
A
B
C
D
三、向量加法的平行四边形法则:
km/h的速度向垂直于对岸的方向行驶,同时河水的流速为
2km/h,求船实际航 行速度的大小与方 向.
A
D
C
B
例2
方法小结:
方法小结:
三角形法则适用于首尾相接的向量求和;而平行四边形法则适用于同起点的两个向量求和;但共线向量求和时,则三角形法则较合适.
例3:下列各式的结果为零向量
的有( )个
例4:利用向量的对角线
思 考:
