人教版八年级下册数学17.1勾股定理 勾股定理的应用课件 (共14张PPT)
文档属性
| 名称 | 人教版八年级下册数学17.1勾股定理 勾股定理的应用课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
人教版
八年级数学下册第十七章
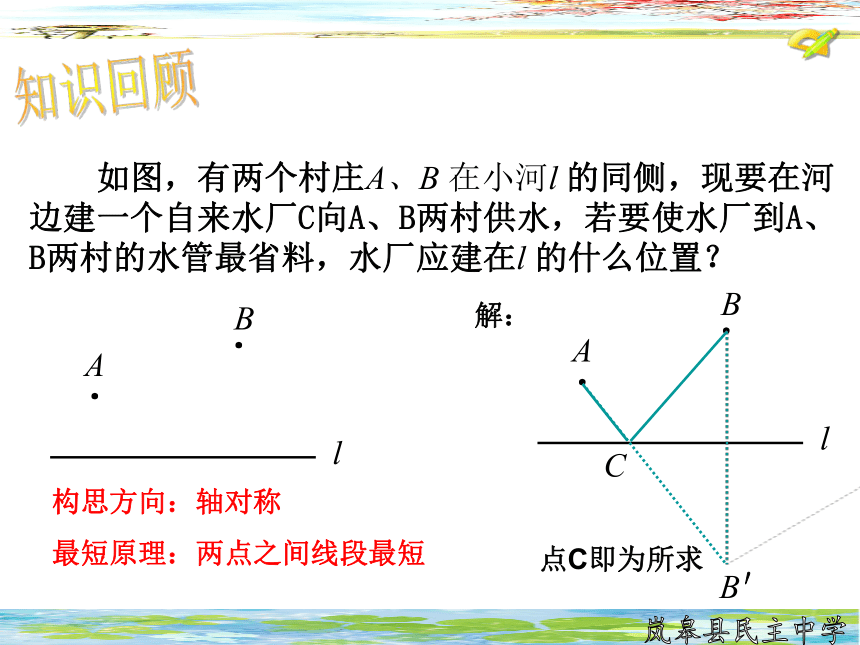
如图,有两个村庄A、B
在小河l
的同侧,现要在河边建一个自来水厂C向A、B两村供水,若要使水厂到A、B两村的水管最省料,水厂应建在l
的什么位置?
构思方向:轴对称
最短原理:两点之间线段最短
点C即为所求
解:
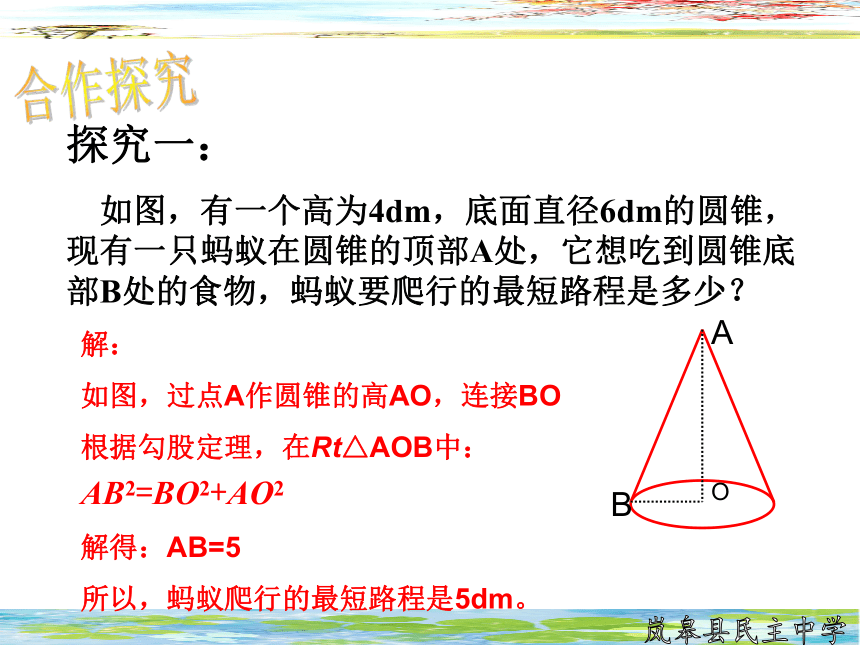
探究一:
如图,有一个高为4dm,底面直径6dm的圆锥,现有一只蚂蚁在圆锥的顶部A处,它想吃到圆锥底部B处的食物,蚂蚁要爬行的最短路程是多少?
A
B
解:
如图,过点A作圆锥的高AO,连接BO
根据勾股定理,在Rt△AOB中:
AB2=BO2+AO2
解得:AB=5
所以,蚂蚁爬行的最短路程是5dm。
O
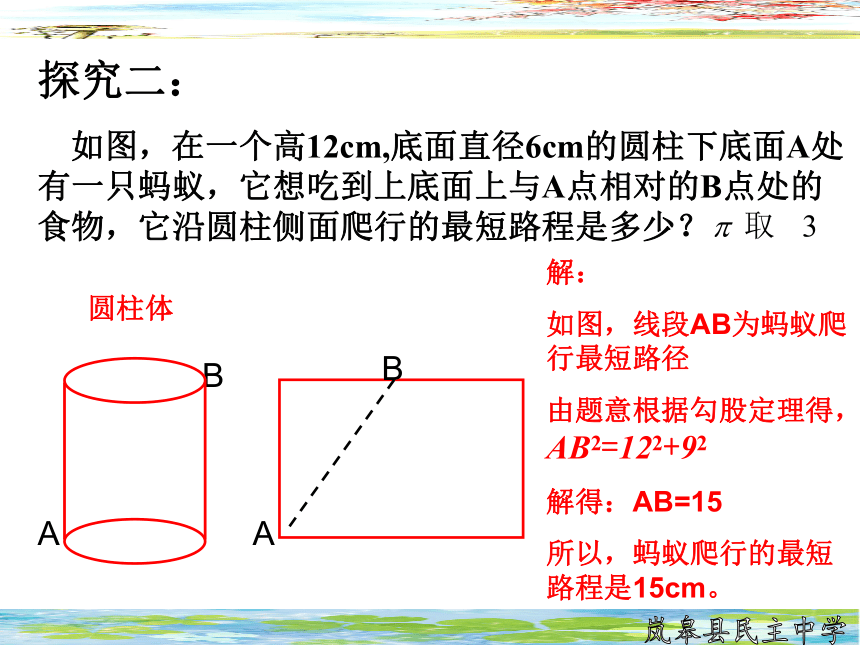
探究二:
如图,在一个高12cm,底面直径6cm的圆柱下底面A处有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它沿圆柱侧面爬行的最短路程是多少?
A
B
解:
如图,线段AB为蚂蚁爬行最短路径
由题意根据勾股定理得,AB2=122+92
解得:AB=15
所以,蚂蚁爬行的最短路程是15cm。
A
B
圆柱体
归纳:
勾股定理实际应用关键在数学的建模
勾股定理应用建模
实际问题转化为数学问题
立体图形转化为平面图形
勾股定理解决问题
构建直角三角形
10
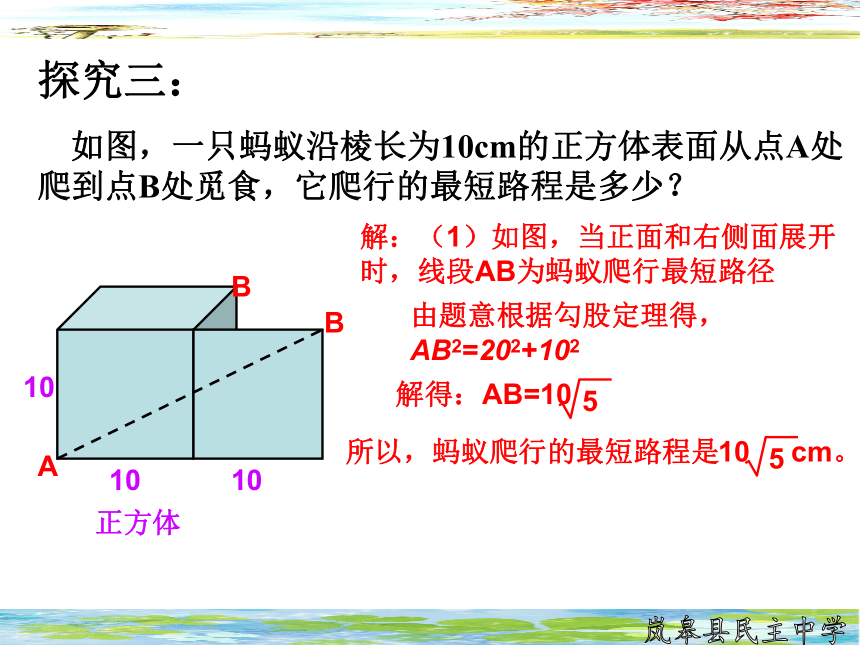
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(1)如图,当正面和右侧面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,AB2=202+102
正方体
10
10
10
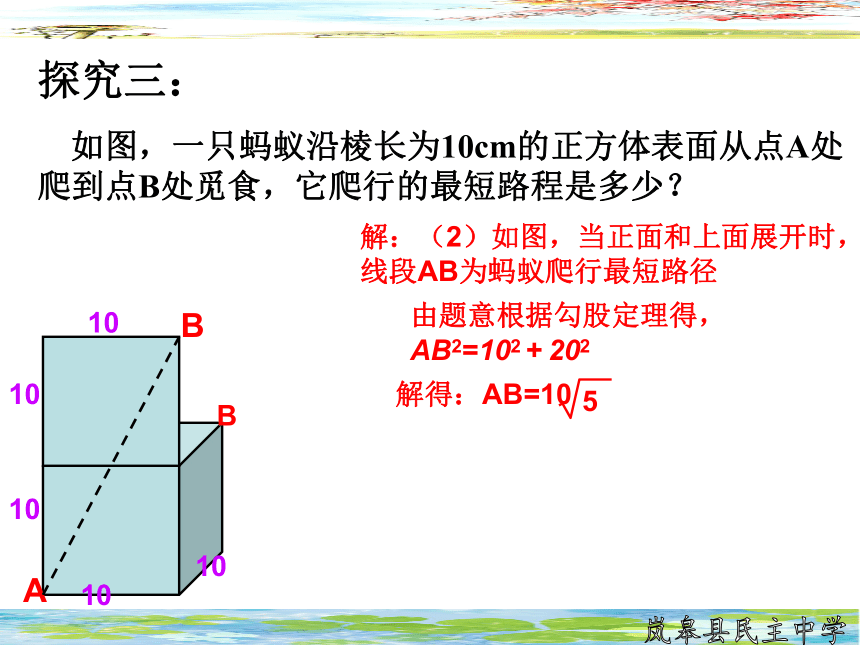
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(2)如图,当正面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,AB2=102
+
202
10
10
10
10
10
B
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(3)如图,当左侧面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
由题意根据勾股定理得,AB2=102
+
202
10
10
10
10
10
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(1)如图,当正面和右侧面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,
AB2=252
+
202
学生独立完成也可小组合作
15
20
10
20
长方体
解:(2)如图,当正面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
由题意根据勾股定理得,
AB2=152
+
302
15
10
20
10
B
解:(3)如图,当左侧面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
由题意根据勾股定理得,
AB2=102
+
352
10
15
20
15
学生独立完成也可小组合作
绩优学案P30:
例1和跟踪训练1
这节课你有事么收获?
1、本节课主要学到了如何利用勾股定理解决立体图形两点之间最短距离问题
2、理解勾股定理实际应用关键在数学的建模,实际问题
数学问题
立体图形
平面图形
课本P39
12题
绩优学案P32
11题
作业:
人教版
八年级数学下册第十七章
如图,有两个村庄A、B
在小河l
的同侧,现要在河边建一个自来水厂C向A、B两村供水,若要使水厂到A、B两村的水管最省料,水厂应建在l
的什么位置?
构思方向:轴对称
最短原理:两点之间线段最短
点C即为所求
解:
探究一:
如图,有一个高为4dm,底面直径6dm的圆锥,现有一只蚂蚁在圆锥的顶部A处,它想吃到圆锥底部B处的食物,蚂蚁要爬行的最短路程是多少?
A
B
解:
如图,过点A作圆锥的高AO,连接BO
根据勾股定理,在Rt△AOB中:
AB2=BO2+AO2
解得:AB=5
所以,蚂蚁爬行的最短路程是5dm。
O
探究二:
如图,在一个高12cm,底面直径6cm的圆柱下底面A处有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它沿圆柱侧面爬行的最短路程是多少?
A
B
解:
如图,线段AB为蚂蚁爬行最短路径
由题意根据勾股定理得,AB2=122+92
解得:AB=15
所以,蚂蚁爬行的最短路程是15cm。
A
B
圆柱体
归纳:
勾股定理实际应用关键在数学的建模
勾股定理应用建模
实际问题转化为数学问题
立体图形转化为平面图形
勾股定理解决问题
构建直角三角形
10
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(1)如图,当正面和右侧面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,AB2=202+102
正方体
10
10
10
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(2)如图,当正面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,AB2=102
+
202
10
10
10
10
10
B
探究三:
如图,一只蚂蚁沿棱长为10cm的正方体表面从点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(3)如图,当左侧面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
由题意根据勾股定理得,AB2=102
+
202
10
10
10
10
10
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
解:(1)如图,当正面和右侧面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
由题意根据勾股定理得,
AB2=252
+
202
学生独立完成也可小组合作
15
20
10
20
长方体
解:(2)如图,当正面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
B
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
由题意根据勾股定理得,
AB2=152
+
302
15
10
20
10
B
解:(3)如图,当左侧面和上面展开时,线段AB为蚂蚁爬行最短路径
A
B
如图,长方体的长为15,宽为10,高为20,一只蚂蚁要从长方体表面点A处爬到点B处觅食,它爬行的最短路程是多少?
由题意根据勾股定理得,
AB2=102
+
352
10
15
20
15
学生独立完成也可小组合作
绩优学案P30:
例1和跟踪训练1
这节课你有事么收获?
1、本节课主要学到了如何利用勾股定理解决立体图形两点之间最短距离问题
2、理解勾股定理实际应用关键在数学的建模,实际问题
数学问题
立体图形
平面图形
课本P39
12题
绩优学案P32
11题
作业:
