人教版八年级下册数学:第17章 勾股定理小结 课件 (共17张PPT)
文档属性
| 名称 | 人教版八年级下册数学:第17章 勾股定理小结 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第17章
勾股定理
小
结
人教版八年级下册
情境引入
1.
会运用勾股定理的数学模型解决现实世界的实际问题.(重点)
2.灵活运用勾股定理进行计算.(难点)
1.直角三角形三边的长有什么关系?找一个实际问题并用勾股定理解决.
2.已知一个三角形的三边,你能判断它是否直角三角形吗?
3.如果一个命题成立,它的逆命题一定成立吗?请举例说明.
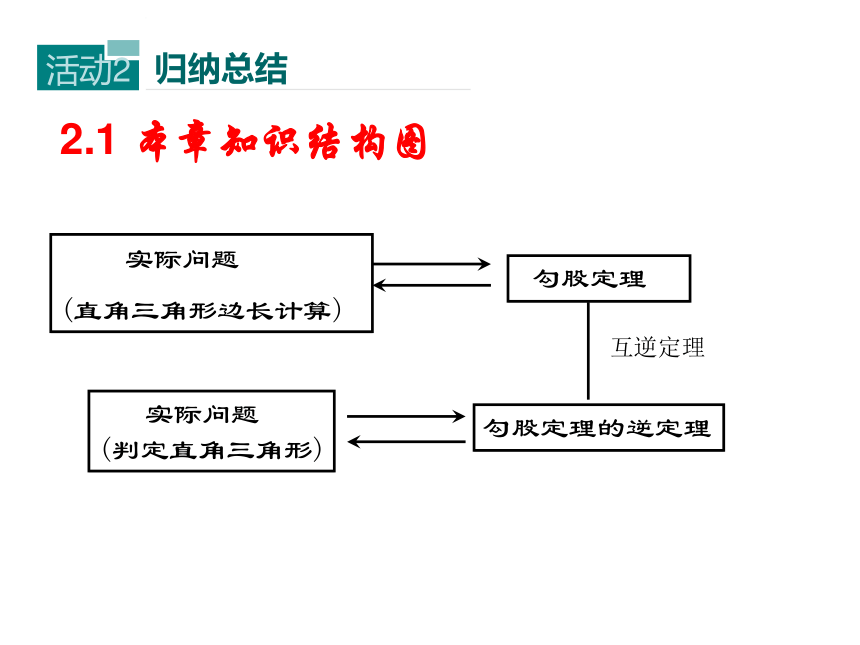
2.1
本章知识结构图
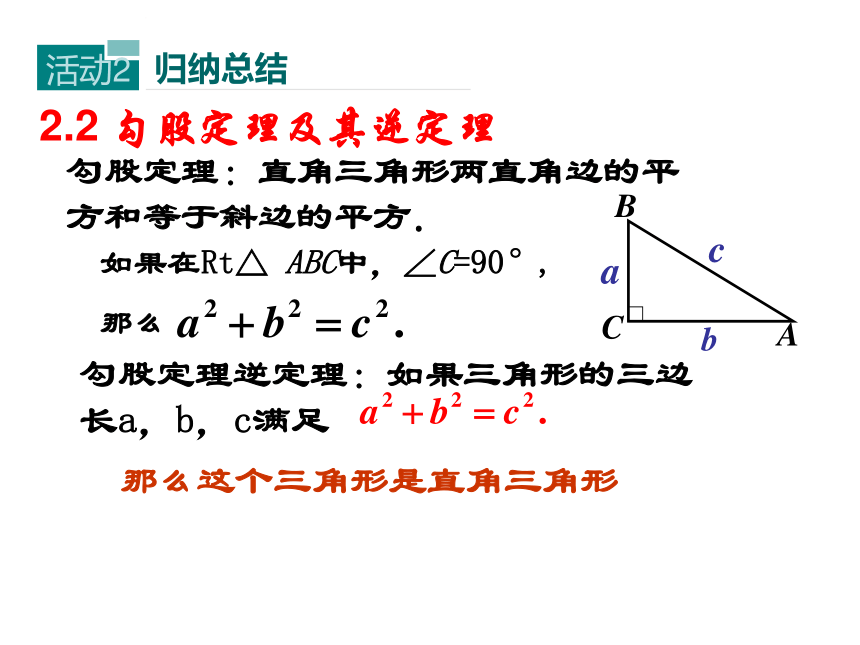
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
勾股定理逆定理:如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形
2.2
勾股定理及其逆定理
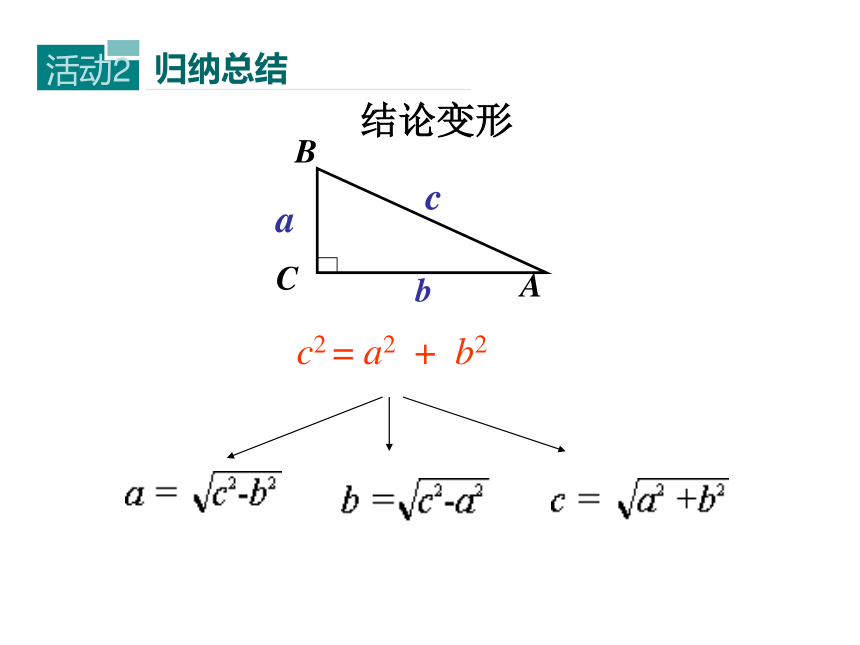
结论变形
c2
=
a2
+
b2
在
Rt△ABC中,∠C=90°
⑴已知a=6,b=8,则c=__
40
⑵已知a=9,c=41,则b=__
⑶已知c=25,b=15,则a=__
20
10
2.3
练习(抢答)
(4).如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.
40
⑴请你观察a,b,c与n之间的关系用含自然数n(n>1)的代数式表示:
a=_________,b=_________,c=_________
⑵猜想:以a,b,c为边的三角形是否为直角三角形?并说明你的猜想。
例1:观
察
下
表
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请用含有n(n为正整数)等式表示上述变化规律的;
(2)推算出OA10长
(3)求值
1
1
例2:细心观察图形,然后回答问题:
1
例3:
如图1所示,为一上面无盖的正方形纸盒,现将其剪开
成平面图,如图2所示,已知展开图中每个正方形的边长为1
⑴求在展开图中可画出最长线段的长度?这样的线段可画几条?
⑵试比较立体图中∠BAC与平面展开图中∠B’A’C’的大小关系?
最长线段共有4条
?
?
例4:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(
取3)是(
)
A.20cm
B.10cm
C.14cm
D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
10
A
例5:
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
x
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3.1米
你能总结规律吗?
B
A
C
D
F
E
例6:
一架秋千,当它静止时,踏板离地1尺,把它往前推送10尺,秋千的踏板就和熊猫一样高,已知熊猫的身高为5尺,如果这时秋千的绳索拉得很直,试问它有多长?
1尺
5尺
X-4
10尺
x
E
E
E
谈一谈,本节课你有哪些收获?
复习题17:
教材第38页复习巩固
第2、3、4题
第17章
勾股定理
小
结
人教版八年级下册
情境引入
1.
会运用勾股定理的数学模型解决现实世界的实际问题.(重点)
2.灵活运用勾股定理进行计算.(难点)
1.直角三角形三边的长有什么关系?找一个实际问题并用勾股定理解决.
2.已知一个三角形的三边,你能判断它是否直角三角形吗?
3.如果一个命题成立,它的逆命题一定成立吗?请举例说明.
2.1
本章知识结构图
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
勾股定理逆定理:如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形
2.2
勾股定理及其逆定理
结论变形
c2
=
a2
+
b2
在
Rt△ABC中,∠C=90°
⑴已知a=6,b=8,则c=__
40
⑵已知a=9,c=41,则b=__
⑶已知c=25,b=15,则a=__
20
10
2.3
练习(抢答)
(4).如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.
40
⑴请你观察a,b,c与n之间的关系用含自然数n(n>1)的代数式表示:
a=_________,b=_________,c=_________
⑵猜想:以a,b,c为边的三角形是否为直角三角形?并说明你的猜想。
例1:观
察
下
表
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请用含有n(n为正整数)等式表示上述变化规律的;
(2)推算出OA10长
(3)求值
1
1
例2:细心观察图形,然后回答问题:
1
例3:
如图1所示,为一上面无盖的正方形纸盒,现将其剪开
成平面图,如图2所示,已知展开图中每个正方形的边长为1
⑴求在展开图中可画出最长线段的长度?这样的线段可画几条?
⑵试比较立体图中∠BAC与平面展开图中∠B’A’C’的大小关系?
最长线段共有4条
?
?
例4:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(
取3)是(
)
A.20cm
B.10cm
C.14cm
D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
10
A
例5:
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
x
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3.1米
你能总结规律吗?
B
A
C
D
F
E
例6:
一架秋千,当它静止时,踏板离地1尺,把它往前推送10尺,秋千的踏板就和熊猫一样高,已知熊猫的身高为5尺,如果这时秋千的绳索拉得很直,试问它有多长?
1尺
5尺
X-4
10尺
x
E
E
E
谈一谈,本节课你有哪些收获?
复习题17:
教材第38页复习巩固
第2、3、4题
