人教版九年级数学下册课件:29.2三视图2 (2课时 共58张PPT)
文档属性
| 名称 | 人教版九年级数学下册课件:29.2三视图2 (2课时 共58张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览









文档简介
(共58张PPT)
物体在日光或灯光的照射下,会在地面、墙壁等处形成影子,影子与物体的形状有密切的关系.
你知道物体的影子是如何形成的吗?
投影所在的平面叫做投影面.某个平面(地面、墙壁等)
照射光线叫做投影线
投影面
投影
投影线
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection)
投影
平行投影
中心投影
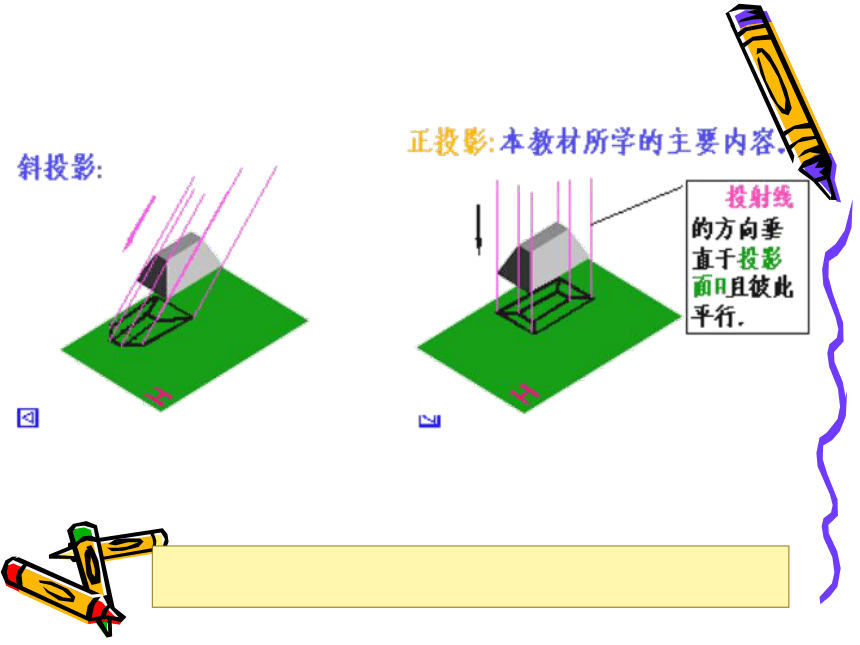
正投影
斜投影
请观察下面三个投影,它们有什么相同与不同的地方?你能试着给正投影下定义吗?
例如:物体在灯泡发出的光照射下形成影子就是中心投影.
由同一点(点光源)发出的光线形成的投影叫做中心投影.
温故知新
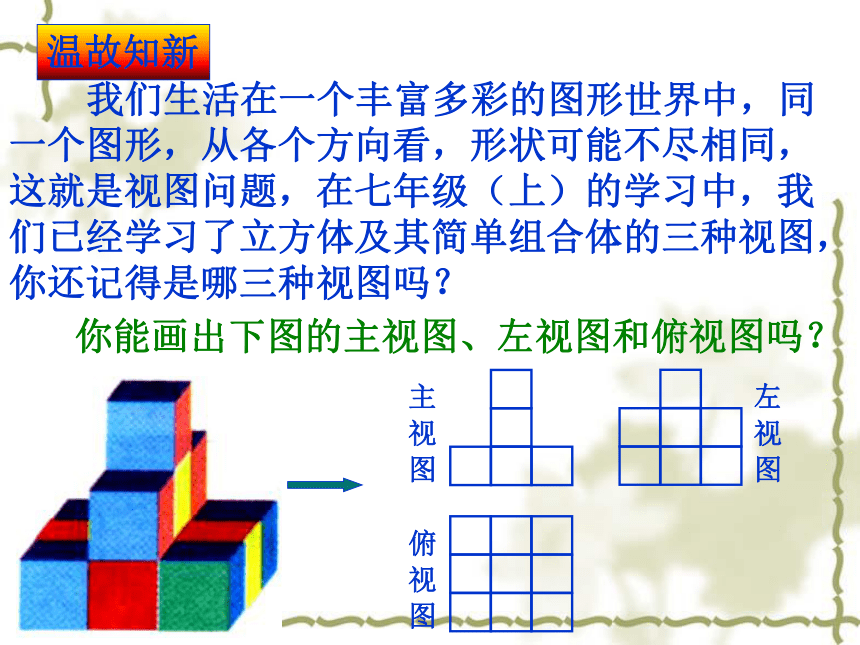
我们生活在一个丰富多彩的图形世界中,同一个图形,从各个方向看,形状可能不尽相同,这就是视图问题,在七年级(上)的学习中,我们已经学习了立方体及其简单组合体的三种视图,你还记得是哪三种视图吗?
你能画出下图的主视图、左视图和俯视图吗?
主 视 图
俯 视 图
左 视 图
三视图
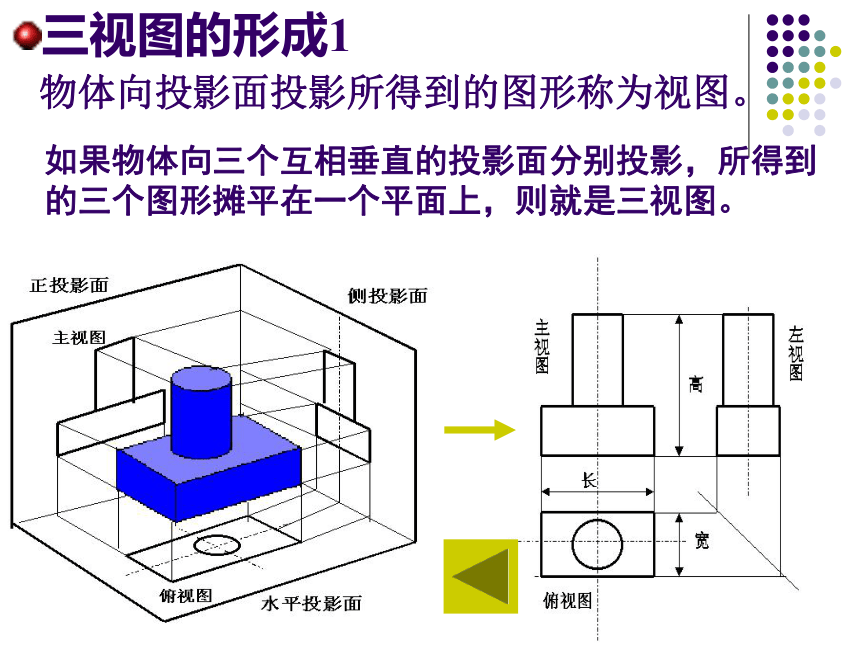
三视图的形成1
物体向投影面投影所得到的图形称为视图。
如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。
三视图的形成2
现将物体放在三面投影体系中,并尽可能使物体的各主要表面平行或垂直与其中的一个投影面,保持物体不动,将物体分别向三个投影面作正投影,就得到物体的三视图。
三视图的名称
从上向下正投影,在投影面得到的投影,称为俯视图(从上向下看)。
从正前向后正投影,在投影面得到的投影,称为主视图(从前向后看);
从左向右正投影,在投影面得到的投影,称为左视图(从左向右看) ;
主视图
左视图
俯视图
长
宽
高
长
高
宽
高
长
宽
长对正,
高平齐,
宽相等.
议一议
⒈下图中物体的形状分别可以看成什么样的几何体?
⒉从正面、侧面、上面看这些几何体,它们的形状各是什么样的?
⒊你能画出各物体的三种视图吗?试试看.
几种基本几何体三视图
圆柱、圆锥、球的三视图
几何体 主视图 左视图 俯视图
·
点不要漏画哦!
想一想
如图是一个蒙古包的照片.你认为这个蒙古包可以看成怎样的几何体?你能画出这个几何体的三种视图吗?
1、球体的投影
球是圆的母线绕其直径所在直线旋转轴旋转而成的。球的三面投影均为圆,且与球的直径相等。
2、圆锥体的投影
圆锥体是由圆锥侧面和底面所围成的立体图形。圆锥面是一条母线绕与它相交的旋转轴旋转而成的。
旋转轴
母线
3、圆柱体的投影
母线
旋转轴
水平投影为一圆,反映顶、底圆的图形,
圆柱面上所有竖线都积聚在该圆周上。
A
B
D
C
4、棱柱体的投影
1、分析:
2、作图:
作图时先画反映底面图形的那个投影,然后再画其它两面投影。
A
A1
B1
C1
F1
B
C
D
E
F
a(a1)
b(b1)
c(c1)
d(d1)
e(e1)
f(f1)
a`(e`)
b`(d`)
a1`(e1`)
f `
c`
f1`
c1`
b1`(d1`)
你能想象出下面各几何体的主视图,左视图,俯视图吗?
我思我进步
1
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
空间想象力
2
三视图
主视图
宽
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
宽
主视图
左视图
俯视图
例、画下例几何体的三视图
例、画下例几何体的三视图
延伸拓展
回味无穷
三视图
主视图——从正面看到的图
左视图——从左面实物的三视图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
我思我进步
⒊根据下列主视图和俯视图,找出对应的物体.
空间想象力
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
俯视图(1)
俯视图(2)
俯视图(3)
俯视图(4)
主视图
左视图
主视图
左视图
俯视图(1)
俯视图(2)
驶向胜利彼岸
空间想象力
主视图
左视图
俯视图(3)
主视图
左视图
俯视图(4)
驶向胜利彼岸
空间想象力
根据如图右边的椅子的视图,工人就能制造出符合设计要求的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广泛的应用.
下面所给的三视图表示什么几何体
直四棱柱
下面所给的三视图表示什么几何体
直五棱柱
下面所给的三视图表示什么几何体
圆锥
下面所给的三视图表示什么几何体
下面所给的三视图表示什么几何体
下面所给的三视图表示什么几何体
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
三棱锥
下面是一个物体的三视图,试说出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
俯视图
左视图
探究
根据三视图想它的立体图形,它是由几块小正方体组成的?
3
2
1
做一做:由几个相同的小立方块搭成的几何体的俯视图如图所示。方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图。
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
3
2
1
4
2
主视图
左视图
1
2
3
4
2
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
主视图
左视图
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭法(你可以用实物模型动手试一试) 你能用三视图表示你探究的结果吗
图3-25
探究活动
用小方块搭一个几何体,使得它的主视图和俯视图如图所示:
请你摆一摆,你会发现些什么?
想一想,摆一摆
⒉由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
由三视图描述几何体(或实物原型),一般先根据各视图想像从各个方向看到的几何体形状, 然后综合起来确定几何体(或实物原型)的形状, 再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢
已知一个几何体的三视图如图3-23所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的数据求出它的侧面积(精确到0.1cm2)
9cm
6cm
4.5cm
3cm
由主视图、左视图知道,这个几何体是直棱柱, 但不能确定棱的条数. 再由俯视图可以确定它是直四棱柱,且底面是梯形.
图3-23
图3-24
3
2
1
课内练习
1.某两个物体的三视图如图所示.请分别说出它们的形状.
正四棱锥
直三棱柱
2.由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
3.一个几何体的三个视图都是全等的正方形, 则这个几何体是______.
4.一个几何体的三视图都是半径相等的圆,则这个几何体是_______.
5.一个几何体的主视图和左视图如图所示,它是什么几何体 请补画这个几何体的俯视图.
6.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(第5题)
(第6题)
立方体
球
直五棱柱,底面是五边形
直三棱柱
用小立方块搭一个几何体,使得它的主视图如图所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试。
动手实践
⒉根据图4、图5的视图,你能分别想像出物体的大致形状吗?
主视图
图4
俯视图
主视图
图5
左视图
⒊根据图6、图7的视图,你能分别想像出物体的大致形状吗?
主视图
图 6
左视图
俯视图
主视图
左视图
俯视图
图 7
由此,你能得出什么结论?
知识 回顾
GO
长
宽
高
长
高
宽
左视图
主视图
俯视图
高
长
宽
返回
B:虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画物体的三视图时,要符合如下原则:
A:大小:长对正(主视图与俯视图),高平齐(主视图与左视图),宽相等(左视图与俯视图).
画三视图是培养空间想象力的一个重要途径.
在挑战自我的平台(由物体画三视图,反过来由三视图想象实物的形状)充分展现自我才华.
物体在日光或灯光的照射下,会在地面、墙壁等处形成影子,影子与物体的形状有密切的关系.
你知道物体的影子是如何形成的吗?
投影所在的平面叫做投影面.某个平面(地面、墙壁等)
照射光线叫做投影线
投影面
投影
投影线
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection)
投影
平行投影
中心投影
正投影
斜投影
请观察下面三个投影,它们有什么相同与不同的地方?你能试着给正投影下定义吗?
例如:物体在灯泡发出的光照射下形成影子就是中心投影.
由同一点(点光源)发出的光线形成的投影叫做中心投影.
温故知新
我们生活在一个丰富多彩的图形世界中,同一个图形,从各个方向看,形状可能不尽相同,这就是视图问题,在七年级(上)的学习中,我们已经学习了立方体及其简单组合体的三种视图,你还记得是哪三种视图吗?
你能画出下图的主视图、左视图和俯视图吗?
主 视 图
俯 视 图
左 视 图
三视图
三视图的形成1
物体向投影面投影所得到的图形称为视图。
如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。
三视图的形成2
现将物体放在三面投影体系中,并尽可能使物体的各主要表面平行或垂直与其中的一个投影面,保持物体不动,将物体分别向三个投影面作正投影,就得到物体的三视图。
三视图的名称
从上向下正投影,在投影面得到的投影,称为俯视图(从上向下看)。
从正前向后正投影,在投影面得到的投影,称为主视图(从前向后看);
从左向右正投影,在投影面得到的投影,称为左视图(从左向右看) ;
主视图
左视图
俯视图
长
宽
高
长
高
宽
高
长
宽
长对正,
高平齐,
宽相等.
议一议
⒈下图中物体的形状分别可以看成什么样的几何体?
⒉从正面、侧面、上面看这些几何体,它们的形状各是什么样的?
⒊你能画出各物体的三种视图吗?试试看.
几种基本几何体三视图
圆柱、圆锥、球的三视图
几何体 主视图 左视图 俯视图
·
点不要漏画哦!
想一想
如图是一个蒙古包的照片.你认为这个蒙古包可以看成怎样的几何体?你能画出这个几何体的三种视图吗?
1、球体的投影
球是圆的母线绕其直径所在直线旋转轴旋转而成的。球的三面投影均为圆,且与球的直径相等。
2、圆锥体的投影
圆锥体是由圆锥侧面和底面所围成的立体图形。圆锥面是一条母线绕与它相交的旋转轴旋转而成的。
旋转轴
母线
3、圆柱体的投影
母线
旋转轴
水平投影为一圆,反映顶、底圆的图形,
圆柱面上所有竖线都积聚在该圆周上。
A
B
D
C
4、棱柱体的投影
1、分析:
2、作图:
作图时先画反映底面图形的那个投影,然后再画其它两面投影。
A
A1
B1
C1
F1
B
C
D
E
F
a(a1)
b(b1)
c(c1)
d(d1)
e(e1)
f(f1)
a`(e`)
b`(d`)
a1`(e1`)
f `
c`
f1`
c1`
b1`(d1`)
你能想象出下面各几何体的主视图,左视图,俯视图吗?
我思我进步
1
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
空间想象力
2
三视图
主视图
宽
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
宽
主视图
左视图
俯视图
例、画下例几何体的三视图
例、画下例几何体的三视图
延伸拓展
回味无穷
三视图
主视图——从正面看到的图
左视图——从左面实物的三视图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
我思我进步
⒊根据下列主视图和俯视图,找出对应的物体.
空间想象力
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
俯视图(1)
俯视图(2)
俯视图(3)
俯视图(4)
主视图
左视图
主视图
左视图
俯视图(1)
俯视图(2)
驶向胜利彼岸
空间想象力
主视图
左视图
俯视图(3)
主视图
左视图
俯视图(4)
驶向胜利彼岸
空间想象力
根据如图右边的椅子的视图,工人就能制造出符合设计要求的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广泛的应用.
下面所给的三视图表示什么几何体
直四棱柱
下面所给的三视图表示什么几何体
直五棱柱
下面所给的三视图表示什么几何体
圆锥
下面所给的三视图表示什么几何体
下面所给的三视图表示什么几何体
下面所给的三视图表示什么几何体
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
三棱锥
下面是一个物体的三视图,试说出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
俯视图
左视图
探究
根据三视图想它的立体图形,它是由几块小正方体组成的?
3
2
1
做一做:由几个相同的小立方块搭成的几何体的俯视图如图所示。方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图。
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
3
2
1
4
2
主视图
左视图
1
2
3
4
2
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
主视图
左视图
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭法(你可以用实物模型动手试一试) 你能用三视图表示你探究的结果吗
图3-25
探究活动
用小方块搭一个几何体,使得它的主视图和俯视图如图所示:
请你摆一摆,你会发现些什么?
想一想,摆一摆
⒉由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
由三视图描述几何体(或实物原型),一般先根据各视图想像从各个方向看到的几何体形状, 然后综合起来确定几何体(或实物原型)的形状, 再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢
已知一个几何体的三视图如图3-23所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的数据求出它的侧面积(精确到0.1cm2)
9cm
6cm
4.5cm
3cm
由主视图、左视图知道,这个几何体是直棱柱, 但不能确定棱的条数. 再由俯视图可以确定它是直四棱柱,且底面是梯形.
图3-23
图3-24
3
2
1
课内练习
1.某两个物体的三视图如图所示.请分别说出它们的形状.
正四棱锥
直三棱柱
2.由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
3.一个几何体的三个视图都是全等的正方形, 则这个几何体是______.
4.一个几何体的三视图都是半径相等的圆,则这个几何体是_______.
5.一个几何体的主视图和左视图如图所示,它是什么几何体 请补画这个几何体的俯视图.
6.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(第5题)
(第6题)
立方体
球
直五棱柱,底面是五边形
直三棱柱
用小立方块搭一个几何体,使得它的主视图如图所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试。
动手实践
⒉根据图4、图5的视图,你能分别想像出物体的大致形状吗?
主视图
图4
俯视图
主视图
图5
左视图
⒊根据图6、图7的视图,你能分别想像出物体的大致形状吗?
主视图
图 6
左视图
俯视图
主视图
左视图
俯视图
图 7
由此,你能得出什么结论?
知识 回顾
GO
长
宽
高
长
高
宽
左视图
主视图
俯视图
高
长
宽
返回
B:虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画物体的三视图时,要符合如下原则:
A:大小:长对正(主视图与俯视图),高平齐(主视图与左视图),宽相等(左视图与俯视图).
画三视图是培养空间想象力的一个重要途径.
在挑战自我的平台(由物体画三视图,反过来由三视图想象实物的形状)充分展现自我才华.
