鲁教版八年级数学下册 第九章 图形的相似测试题(含答案)
文档属性
| 名称 | 鲁教版八年级数学下册 第九章 图形的相似测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 09:30:17 | ||
图片预览



文档简介
第九章
图形的相似测试题
一、选择题(每小题3分,共30分)
1.△ABC的三边之比为3:4:5,与其相似的△DEF的最短边是9
cm,则其最长边的长是( )
C
A.5
cm
B.10
cm
C.15
cm
D.30
cm
2.下列四个命题中,假命题是(
)
A.有一个锐角相等的两个等腰三角形相似
B.有一个锐角相等的两个直角三角形相似
C.底边和腰对应成比例的两个等腰三角形相似
D.斜边和直角边对应成比例的两个直角三角形相似
3.小明身高1.5米,在操场上的影长为2米,同时测得教学大楼在操场上的影长为60米,则教学大楼的高度应为( )
A
A.45米
B.40米
C.90米
D.80米
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,需要添加一个条件,下列添加不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
=
D.
=
SHAPE
\
MERGEFORMAT
第4题图
第6题图
5.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
6.
如图,在平行四边形ABCD中,EF∥AB交AD于点E,交BD于点F,DE∶EA=3∶4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
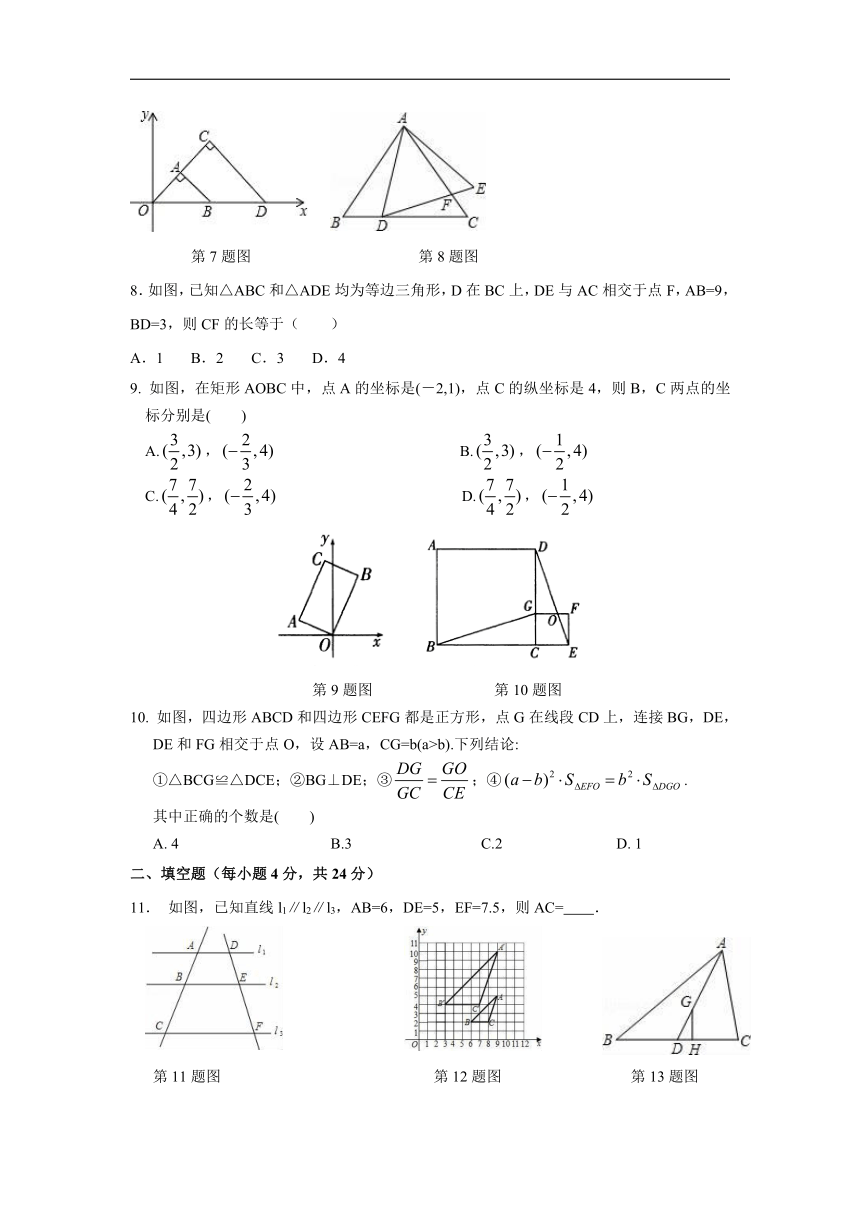
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
第7题图
第8题图
8.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF的长等于( )
A.1
B.2
C.3
D.4
9.
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是(
)
A.,
B.,
C.,
D.,
第9题图
第10题图
10.
如图,四边形ABCD和四边形CEFG都是正方形,点G在线段CD上,连接BG,DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:
①△BCG≌△DCE;②BG⊥DE;③;④.
其中正确的个数是(
)
A.
4
B.3
C.2
D.
1
二、填空题(每小题4分,共24分)
11.
如图,已知直线l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
第11题图
第12题图
第13题图
12.
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
13.如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=3,则点A到BC的距离为 .
14.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边的长分别为DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB= m.
第14题图
第15题图
第16题图
15.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
16.
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为 .
三、解答题(共66分)
17.
(6分)如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
SHAPE
\
MERGEFORMAT
第17题图
第18题图
18.
(8分)如图,△ABC中,CD是AB边上的高,且=.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
19.
(10分)如图,△ABC三个顶点的坐标分别为A(0,﹣3),B(3,﹣2),C(2,﹣4),正方形网格中,每个小正方形的边长均是1个单位长度.以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的相似比为2∶1,并直接写出点A1的坐标.
20.(10分)如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的,若AB=2,求△ABC移动的距离BE的长.
第20题图
21.(10分)
(?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?65abad3e-b61d-49bc-89f7-7123055ccc36"
\t
"_blank?)如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长.
第21题图
第22题图
22.
(10分)如图,在平行四边形ABCD中,对角线AC,BD交于点O,M为AD的中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
23.(12分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图,已知标杆的高度CD=3
m,标杆与旗杆的水平距离BD=15
m,人的眼睛离地面的高度EF=1.6
m,人与标杆CD的水平距离FD=2
m,求旗杆AB的高度.
附加题(20分,不计入总分)
24.
如图,在平面直角坐标系xOy中,直线y=-x+3与轴交于点C,与直线AD交于点,点D的坐标为(0,1)
.
(1)求直线AD的函数表达式;
(2)设直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
参考答案:
第九章
图形的相似测试题
一、1.C
2.A
3.A
4.D
5.D
6.B
7.B
8.B
9.B
10.B
二、11.15
12.(9,0)
13.9
14.5.5
15.
4或9
16.
(﹣8,﹣3)或(4,3)
三、17.(1)证明:因为四边形ABCD是矩形,所以AD∥BC,所以∠DAE=∠AMB.
又因为∠DEA=∠B=90°,所以△ADE∽△MAB.
(2)解:由(1)知△ADE∽△MAB,所以DE∶AD=AB∶MA.
因为M是边BC的中点,BC=6,所以BM=3.
又因为AB=4,∠B=90°,所以AM=5,所以DE∶6=4∶5,所以DE=.
18.(1)证明:因为CD是AB边上的高,所以∠ADC=∠CDB=90°.
又因为=,所以△ACD∽△CBD.
(2)解:因为△ACD∽△CBD,所以∠A=∠BCD.
因为∠ADC=90°,所以∠A+∠ACD=90°,所以∠BCD+∠ACD=90°,即∠ACB=90°.
19.解:如图所示,△A1B1C1即为所求,点A1的坐标为(﹣2,﹣2).
SHAPE
\
MERGEFORMAT
第19题图
20.解:由平移得EF∥AC,所以△BEG∽△BAC,所以.
又AB=2,所以BE=.
21.解:因为AB⊥BC,所以∠B=90°.因为AD∥BC,所以∠A=180°﹣∠B=90°.
所以∠PAD=∠PBC=90°. AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,
解得x=;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),
解得x=2或x=6.
所以AP=
或AP=2或AP=6.
22.解:(1)因为四边形ABCD是平行四边形,所以AD∥BC,AD=BC,OB=OD,
所以∠DMN=∠BCN,∠MDN=∠NBC,所以△MND∽△CNB,所以=.
因为M为AD的中点,所以MD=AD=BC,即=.
所以=,即BN=2DN.
设OB=
x,则BN=x+1,DN=x﹣1,所以x+1=2(x﹣1),解得x=3.
所以BD=2x=6.
(2)因为△MND∽△CNB,且相似比为1∶2,所以MN∶CN=DN∶BN=1∶2,
所以S△MND=S△CND=1,S△BNC=4S△MND=4.
所以S△ABD=S△BCD=
6,所以S四边形ABNM=S△ABD﹣S△MND=6﹣1=5.
解:作EH⊥AB于点H,交CD于点G.
因为CD⊥FB,AB⊥FB,所以CD∥AB.
易得△CGE∽△AHE,所以,即
即解得AH=11.9,
所以AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
所以旗杆AB的高度为13.5m.
24.(1)y=x+1.
(2)因为点E在直线AD上,所以可设点E的坐标为(m,
m+1).
令,得x=-2.所以点B的坐标为(-2,0).
令y=-x+3=0,得x=3,所以点C的坐标为(3,0).
所以OB=2,
OD=1,
BC=5,
BD=.
当△BOD∽△BCE时,如图①所示,则,
即.所以CE=.所以m+1=,解得m=3.所以此时点E的坐标为(3,).
①
②
当△BOD∽△BEC时,如图②所示,过点E作EFBC于点F,则,即.
所以EC=.所以BE=.
因为BE·CE=EF·BC,所以=5EF,则
EF=2.
所以,
解得m=2.所以此时E点的坐标为(2,2).
综上,满足条件的点E的坐标为(3,),(2,2).
图形的相似测试题
一、选择题(每小题3分,共30分)
1.△ABC的三边之比为3:4:5,与其相似的△DEF的最短边是9
cm,则其最长边的长是( )
C
A.5
cm
B.10
cm
C.15
cm
D.30
cm
2.下列四个命题中,假命题是(
)
A.有一个锐角相等的两个等腰三角形相似
B.有一个锐角相等的两个直角三角形相似
C.底边和腰对应成比例的两个等腰三角形相似
D.斜边和直角边对应成比例的两个直角三角形相似
3.小明身高1.5米,在操场上的影长为2米,同时测得教学大楼在操场上的影长为60米,则教学大楼的高度应为( )
A
A.45米
B.40米
C.90米
D.80米
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,需要添加一个条件,下列添加不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
=
D.
=
SHAPE
\
MERGEFORMAT
第4题图
第6题图
5.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
6.
如图,在平行四边形ABCD中,EF∥AB交AD于点E,交BD于点F,DE∶EA=3∶4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
第7题图
第8题图
8.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF的长等于( )
A.1
B.2
C.3
D.4
9.
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是(
)
A.,
B.,
C.,
D.,
第9题图
第10题图
10.
如图,四边形ABCD和四边形CEFG都是正方形,点G在线段CD上,连接BG,DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:
①△BCG≌△DCE;②BG⊥DE;③;④.
其中正确的个数是(
)
A.
4
B.3
C.2
D.
1
二、填空题(每小题4分,共24分)
11.
如图,已知直线l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
第11题图
第12题图
第13题图
12.
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
13.如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=3,则点A到BC的距离为 .
14.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边的长分别为DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB= m.
第14题图
第15题图
第16题图
15.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
16.
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为 .
三、解答题(共66分)
17.
(6分)如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
SHAPE
\
MERGEFORMAT
第17题图
第18题图
18.
(8分)如图,△ABC中,CD是AB边上的高,且=.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
19.
(10分)如图,△ABC三个顶点的坐标分别为A(0,﹣3),B(3,﹣2),C(2,﹣4),正方形网格中,每个小正方形的边长均是1个单位长度.以点C为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的相似比为2∶1,并直接写出点A1的坐标.
20.(10分)如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的,若AB=2,求△ABC移动的距离BE的长.
第20题图
21.(10分)
(?http:?/??/?www.jyeoo.com?/?math?/?report?/?detail?/?65abad3e-b61d-49bc-89f7-7123055ccc36"
\t
"_blank?)如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长.
第21题图
第22题图
22.
(10分)如图,在平行四边形ABCD中,对角线AC,BD交于点O,M为AD的中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
23.(12分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图,已知标杆的高度CD=3
m,标杆与旗杆的水平距离BD=15
m,人的眼睛离地面的高度EF=1.6
m,人与标杆CD的水平距离FD=2
m,求旗杆AB的高度.
附加题(20分,不计入总分)
24.
如图,在平面直角坐标系xOy中,直线y=-x+3与轴交于点C,与直线AD交于点,点D的坐标为(0,1)
.
(1)求直线AD的函数表达式;
(2)设直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
参考答案:
第九章
图形的相似测试题
一、1.C
2.A
3.A
4.D
5.D
6.B
7.B
8.B
9.B
10.B
二、11.15
12.(9,0)
13.9
14.5.5
15.
4或9
16.
(﹣8,﹣3)或(4,3)
三、17.(1)证明:因为四边形ABCD是矩形,所以AD∥BC,所以∠DAE=∠AMB.
又因为∠DEA=∠B=90°,所以△ADE∽△MAB.
(2)解:由(1)知△ADE∽△MAB,所以DE∶AD=AB∶MA.
因为M是边BC的中点,BC=6,所以BM=3.
又因为AB=4,∠B=90°,所以AM=5,所以DE∶6=4∶5,所以DE=.
18.(1)证明:因为CD是AB边上的高,所以∠ADC=∠CDB=90°.
又因为=,所以△ACD∽△CBD.
(2)解:因为△ACD∽△CBD,所以∠A=∠BCD.
因为∠ADC=90°,所以∠A+∠ACD=90°,所以∠BCD+∠ACD=90°,即∠ACB=90°.
19.解:如图所示,△A1B1C1即为所求,点A1的坐标为(﹣2,﹣2).
SHAPE
\
MERGEFORMAT
第19题图
20.解:由平移得EF∥AC,所以△BEG∽△BAC,所以.
又AB=2,所以BE=.
21.解:因为AB⊥BC,所以∠B=90°.因为AD∥BC,所以∠A=180°﹣∠B=90°.
所以∠PAD=∠PBC=90°. AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,
解得x=;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),
解得x=2或x=6.
所以AP=
或AP=2或AP=6.
22.解:(1)因为四边形ABCD是平行四边形,所以AD∥BC,AD=BC,OB=OD,
所以∠DMN=∠BCN,∠MDN=∠NBC,所以△MND∽△CNB,所以=.
因为M为AD的中点,所以MD=AD=BC,即=.
所以=,即BN=2DN.
设OB=
x,则BN=x+1,DN=x﹣1,所以x+1=2(x﹣1),解得x=3.
所以BD=2x=6.
(2)因为△MND∽△CNB,且相似比为1∶2,所以MN∶CN=DN∶BN=1∶2,
所以S△MND=S△CND=1,S△BNC=4S△MND=4.
所以S△ABD=S△BCD=
6,所以S四边形ABNM=S△ABD﹣S△MND=6﹣1=5.
解:作EH⊥AB于点H,交CD于点G.
因为CD⊥FB,AB⊥FB,所以CD∥AB.
易得△CGE∽△AHE,所以,即
即解得AH=11.9,
所以AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
所以旗杆AB的高度为13.5m.
24.(1)y=x+1.
(2)因为点E在直线AD上,所以可设点E的坐标为(m,
m+1).
令,得x=-2.所以点B的坐标为(-2,0).
令y=-x+3=0,得x=3,所以点C的坐标为(3,0).
所以OB=2,
OD=1,
BC=5,
BD=.
当△BOD∽△BCE时,如图①所示,则,
即.所以CE=.所以m+1=,解得m=3.所以此时点E的坐标为(3,).
①
②
当△BOD∽△BEC时,如图②所示,过点E作EFBC于点F,则,即.
所以EC=.所以BE=.
因为BE·CE=EF·BC,所以=5EF,则
EF=2.
所以,
解得m=2.所以此时E点的坐标为(2,2).
综上,满足条件的点E的坐标为(3,),(2,2).
