两角和与差的余弦
图片预览




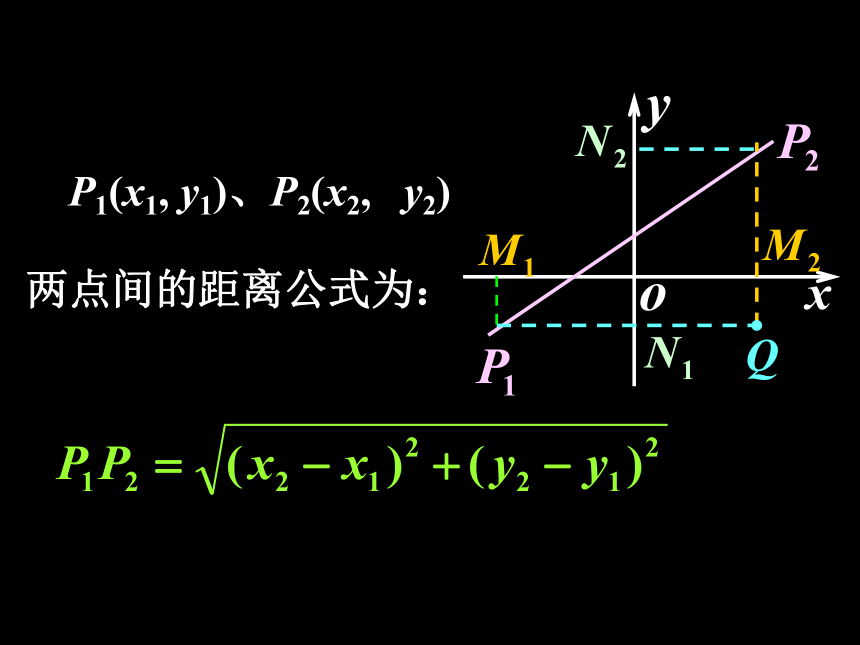







文档简介
(共47张PPT)
两角和与差的余弦
一、平面上的两点间距离公式:
一、平面上的两点间距离公式:
1. 复习:
数轴上两点间的距离公式d=|x1﹣x2|.
一、平面上的两点间距离公式:
1. 复习:
数轴上两点间的距离公式d=|x1﹣x2|.
2. 平面内任意两点P1(x1, y1), P2(x2, y2)
间的距离公式.
P1(x1, y1)、P2(x2, y2)两点间的距离公式为:
二、提供素材,猜想命题:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
2. 由下列等式你又可以猜测出什么呢
2. 由下列等式你又可以猜测出什么呢
2. 由下列等式你又可以猜测出什么呢
三、寻找方法,证明公式:
三、寻找方法,证明公式:
构造以下图形:
三、寻找方法,证明公式:
构造以下图形:
如图: 在平面直 角坐标系内作单位圆 O,并分别作出角α, β, ﹣β, 使得α的始边为 OX , 交圆O于P1,终边 交圆O于P2, β的始边为OP2, 终边交圆O于 P3, ﹣β的始边为OX, 终边交圆O于P4 .
三、寻找方法,证明公式:
构造以下图形:
则:
则:
易知: P1P3= P2P4,
则:
易知: P1P3= P2P4,
由两点距离公式可得:
则:
易知: P1P3= P2P4,
由两点距离公式可得:
展开可得:
展开可得:
展开可得:
即得到两角和的余弦公式, 简称C(α+β).
展开可得:
即得到两角和的余弦公式, 简称C(α+β).
因为α, β为任意角, 故用﹣β代替β 即 可得到两角差的余弦公式:
展开可得:
因为α, β为任意角, 故用﹣β代替β 即 可得到两角差的余弦公式:
即得到两角和的余弦公式, 简称C(α+β).
四、理解公式,初步应用:
四、理解公式,初步应用:
总结诱导公式:
回顾诱导公式:
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
与“奇变偶不变,符号看象限”一致
总 结:
课堂练习
(2005年上海市高考题)
(2004年重庆市高考题)
3. 求值
4. 化简
学法大视野 第25课时
作业布置
两角和与差的余弦
一、平面上的两点间距离公式:
一、平面上的两点间距离公式:
1. 复习:
数轴上两点间的距离公式d=|x1﹣x2|.
一、平面上的两点间距离公式:
1. 复习:
数轴上两点间的距离公式d=|x1﹣x2|.
2. 平面内任意两点P1(x1, y1), P2(x2, y2)
间的距离公式.
P1(x1, y1)、P2(x2, y2)两点间的距离公式为:
二、提供素材,猜想命题:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
二、提供素材,猜想命题:
1. 判断下列等式是否正确:
2. 由下列等式你又可以猜测出什么呢
2. 由下列等式你又可以猜测出什么呢
2. 由下列等式你又可以猜测出什么呢
三、寻找方法,证明公式:
三、寻找方法,证明公式:
构造以下图形:
三、寻找方法,证明公式:
构造以下图形:
如图: 在平面直 角坐标系内作单位圆 O,并分别作出角α, β, ﹣β, 使得α的始边为 OX , 交圆O于P1,终边 交圆O于P2, β的始边为OP2, 终边交圆O于 P3, ﹣β的始边为OX, 终边交圆O于P4 .
三、寻找方法,证明公式:
构造以下图形:
则:
则:
易知: P1P3= P2P4,
则:
易知: P1P3= P2P4,
由两点距离公式可得:
则:
易知: P1P3= P2P4,
由两点距离公式可得:
展开可得:
展开可得:
展开可得:
即得到两角和的余弦公式, 简称C(α+β).
展开可得:
即得到两角和的余弦公式, 简称C(α+β).
因为α, β为任意角, 故用﹣β代替β 即 可得到两角差的余弦公式:
展开可得:
因为α, β为任意角, 故用﹣β代替β 即 可得到两角差的余弦公式:
即得到两角和的余弦公式, 简称C(α+β).
四、理解公式,初步应用:
四、理解公式,初步应用:
总结诱导公式:
回顾诱导公式:
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
(利用以上诱导公式推导下列结论)
公式推广:
与“奇变偶不变,符号看象限”一致
总 结:
课堂练习
(2005年上海市高考题)
(2004年重庆市高考题)
3. 求值
4. 化简
学法大视野 第25课时
作业布置
