平面向量的坐标运算
图片预览




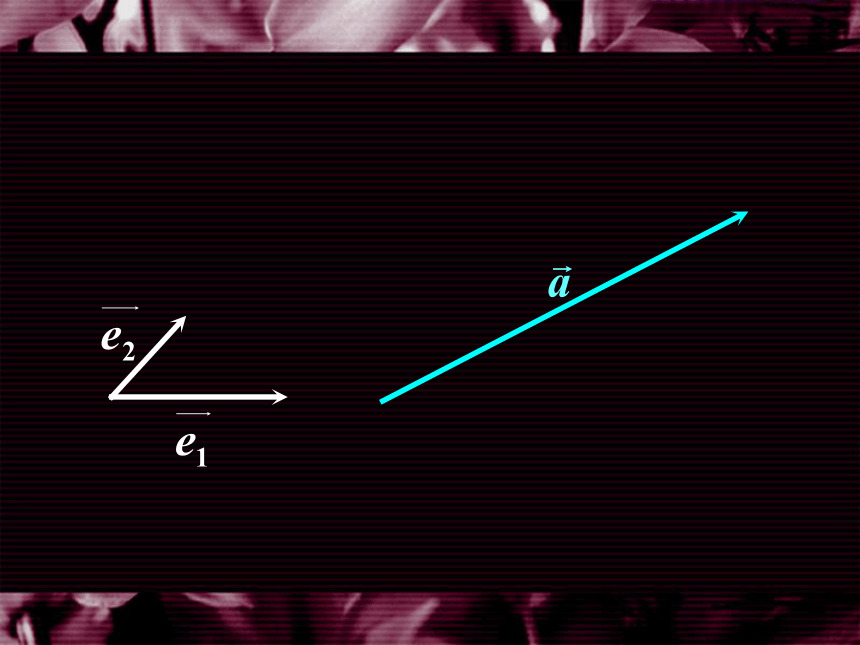
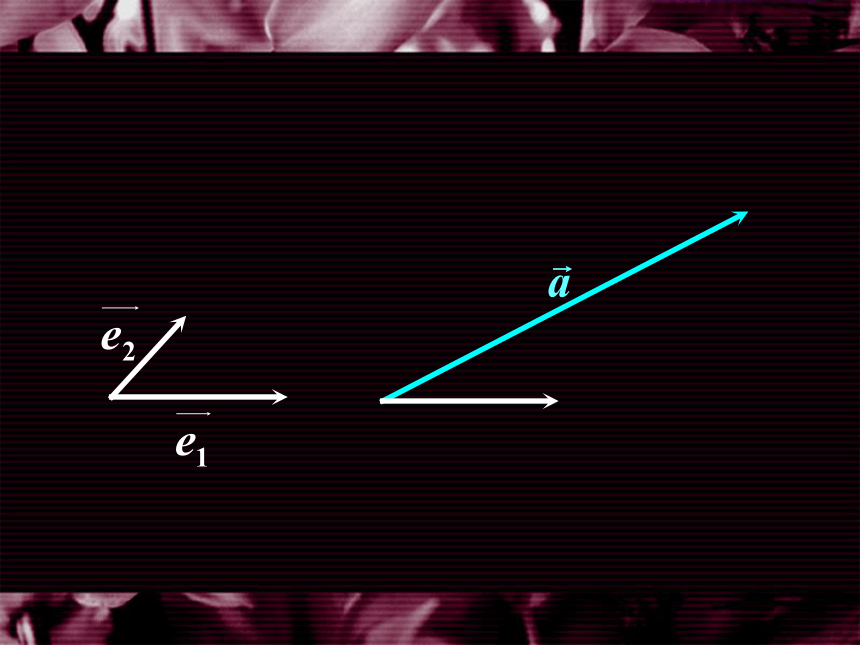
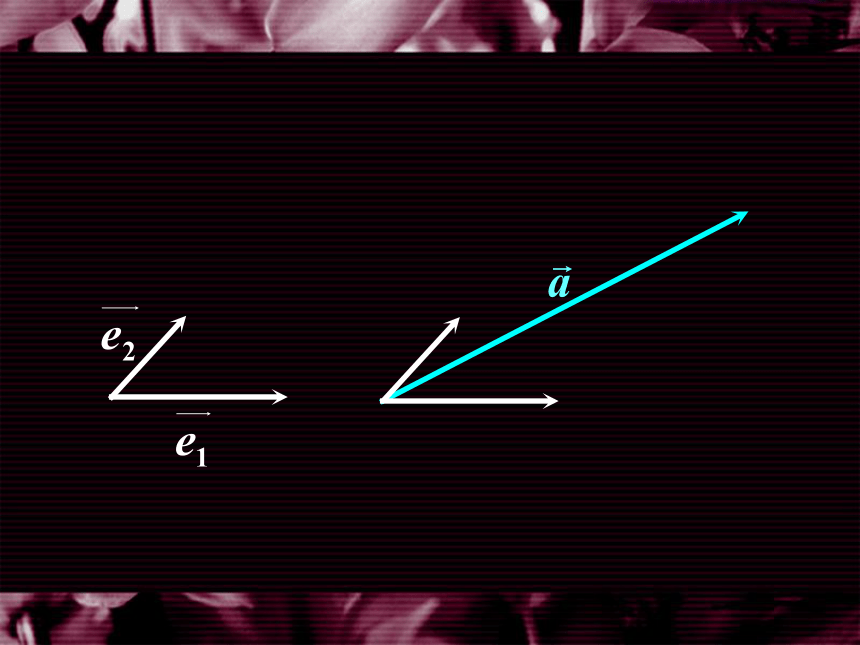
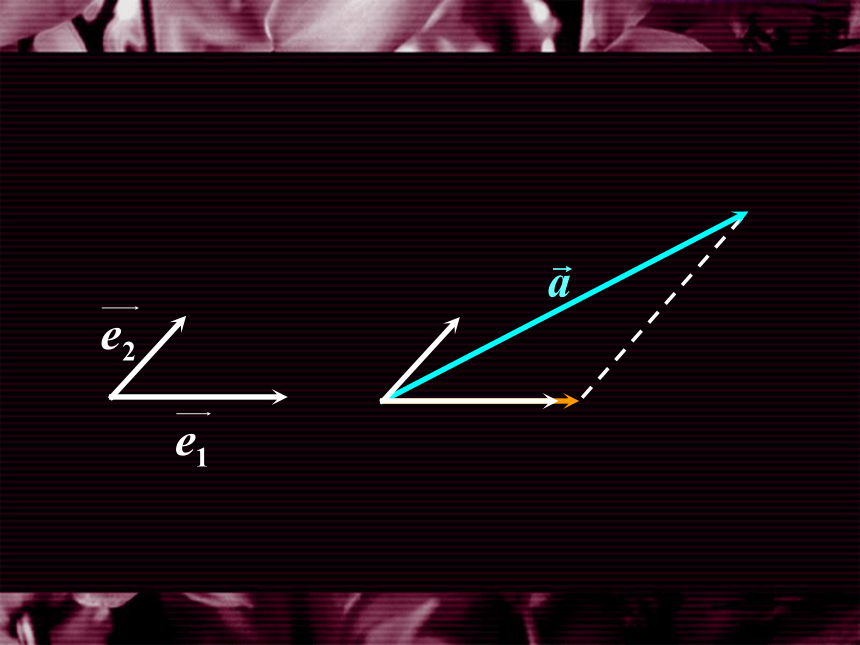
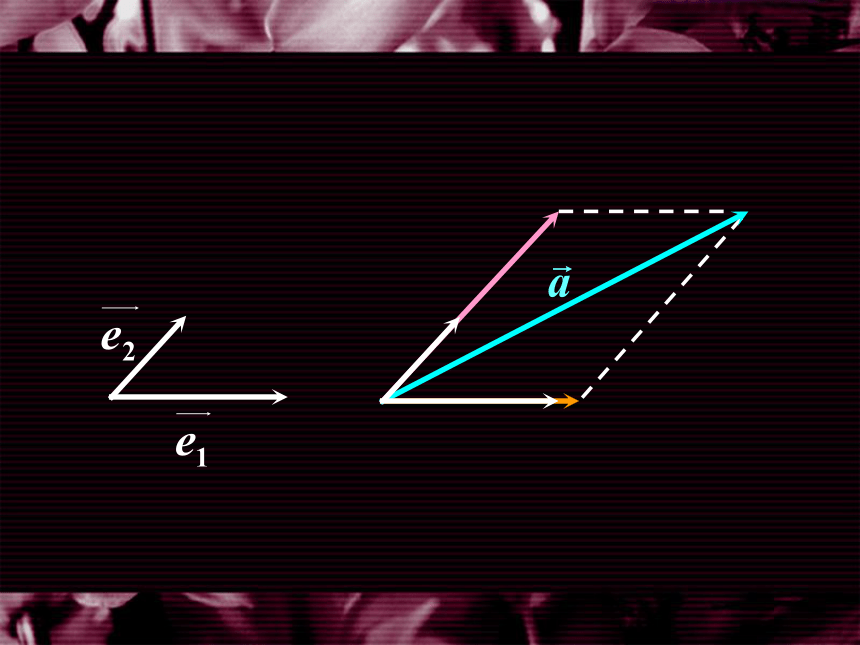
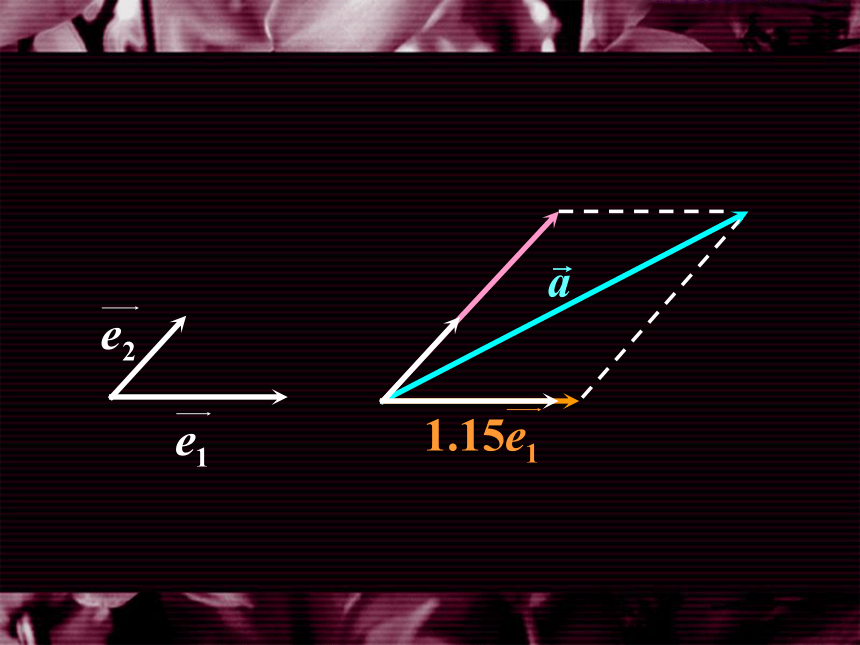
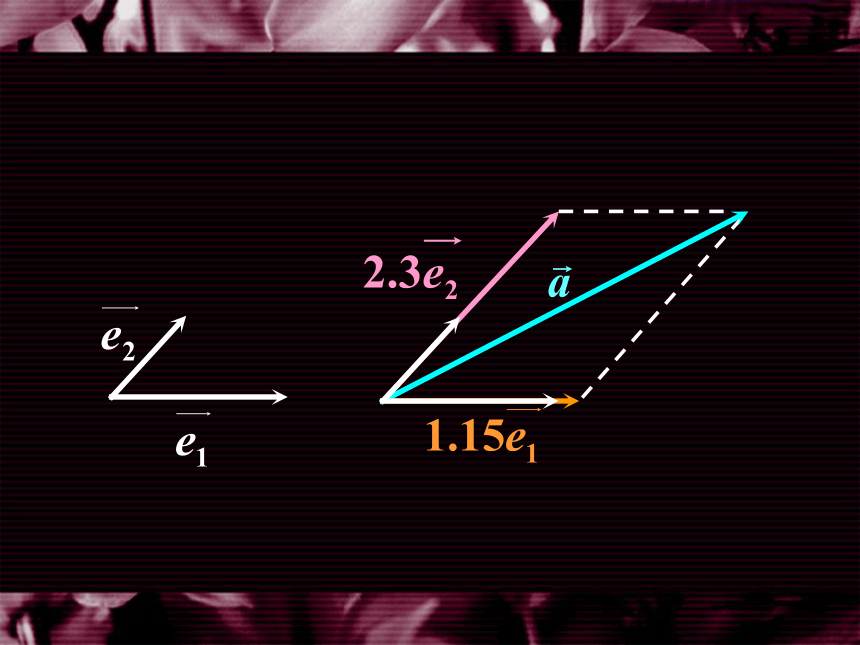
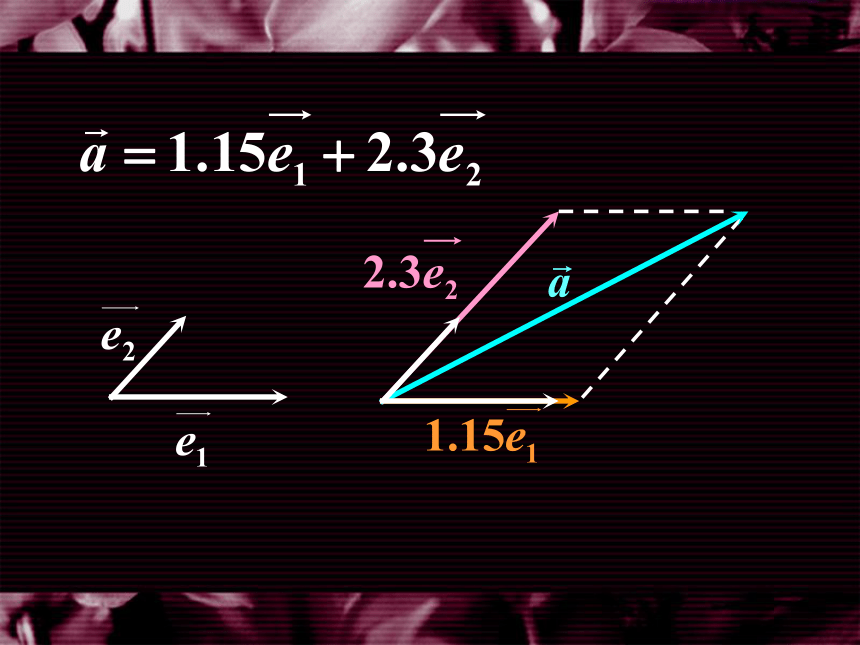
文档简介
(共42张PPT)
平面向量的
提 问
(1) 平面向量的基本定理的内容是什么?
什么叫做平面向量的基底?
提 问
(1) 平面向量的基本定理的内容是什么?
什么叫做平面向量的基底?
提 问
平面向量的正交分解
自学教材 P94~95
在不共线的两个
向量中,垂直是
一种重要的情形。
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解。
F1
O
F2
G
一、平面向量的坐标表示
一、平面向量的坐标表示
O
图 1
一、平面向量的坐标表示
O
图 1
一、平面向量的坐标表示
O
图 1
O
图 1
O
图 1
O
图 1
O
图 1
因此,在平面直角坐标系内, 每一个平面向量 都可以用一对实 数唯一表示.
y
A2
二、平面向量的坐标运算
二、平面向量的坐标运算
二、平面向量的坐标运算
y
x
O
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
y
x
O
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
结论: 一个向量的坐标等于表示此向量的
有向线段的终点的坐标减去始点的坐标.
例: 已知平行四边形ABCD的三个顶点A, B, C的坐标分别为(-2, 1), (-1, 3), (3, 4),求第四个顶点D的坐标.
小 结
1. 引进向量的坐标后,向量的基本
运算转化为实数的基本运算,可
以解方程也可以解不等式。
小 结
2. 要把点的坐标与向量的坐标区分开 来,两者不是一个概念.
2. 要把点的坐标与向量的坐标区分开 来,两者不是一个概念.
学法大视野 第19课时
作业布置
平面向量的
提 问
(1) 平面向量的基本定理的内容是什么?
什么叫做平面向量的基底?
提 问
(1) 平面向量的基本定理的内容是什么?
什么叫做平面向量的基底?
提 问
平面向量的正交分解
自学教材 P94~95
在不共线的两个
向量中,垂直是
一种重要的情形。
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解。
F1
O
F2
G
一、平面向量的坐标表示
一、平面向量的坐标表示
O
图 1
一、平面向量的坐标表示
O
图 1
一、平面向量的坐标表示
O
图 1
O
图 1
O
图 1
O
图 1
O
图 1
因此,在平面直角坐标系内, 每一个平面向量 都可以用一对实 数唯一表示.
y
A2
二、平面向量的坐标运算
二、平面向量的坐标运算
二、平面向量的坐标运算
y
x
O
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
y
x
O
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
B
(
x
2
,
y
2
)
A
(
x
1
,
y
1
)
结论: 一个向量的坐标等于表示此向量的
有向线段的终点的坐标减去始点的坐标.
例: 已知平行四边形ABCD的三个顶点A, B, C的坐标分别为(-2, 1), (-1, 3), (3, 4),求第四个顶点D的坐标.
小 结
1. 引进向量的坐标后,向量的基本
运算转化为实数的基本运算,可
以解方程也可以解不等式。
小 结
2. 要把点的坐标与向量的坐标区分开 来,两者不是一个概念.
2. 要把点的坐标与向量的坐标区分开 来,两者不是一个概念.
学法大视野 第19课时
作业布置
