人教版数学九年级上册24.1.3 弧、弦、圆心角课件(共25张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.3 弧、弦、圆心角课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 14:23:16 | ||
图片预览



文档简介
(共25张PPT)
24.1
圆的有关性质
24.1.3
弧、弦、圆心角
人教版数学九年级上册
3.
理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
1.
理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.
探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
学习目标
【思考】
圆是中心对称图形吗?它的对称中心在哪里?
·
圆心角的概念
探究新知
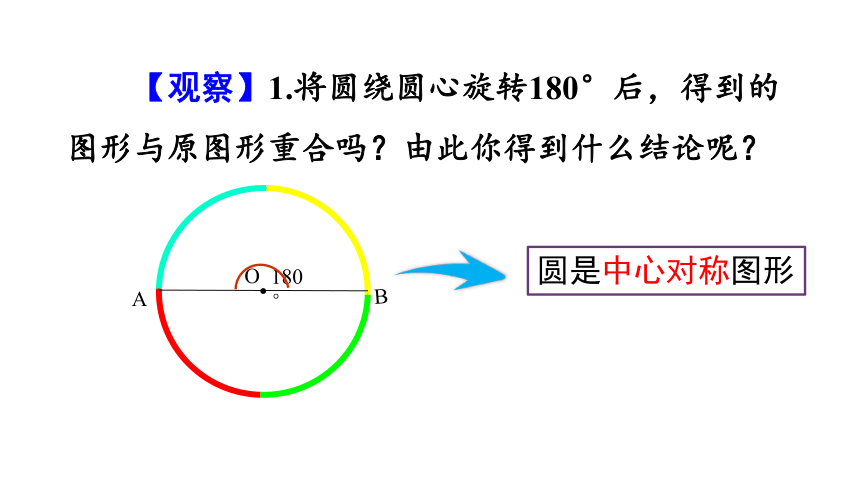
圆是中心对称图形
.
O
A
B
180°
【观察】1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
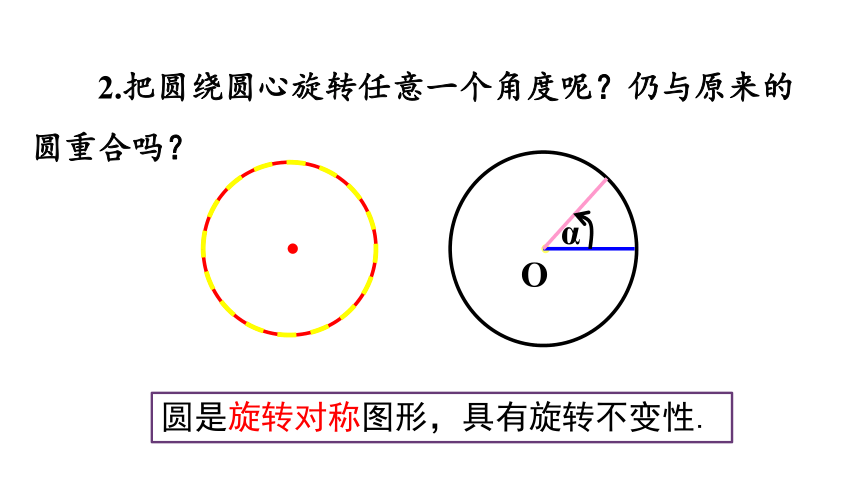
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
·
O
B
A
·
O
B
A
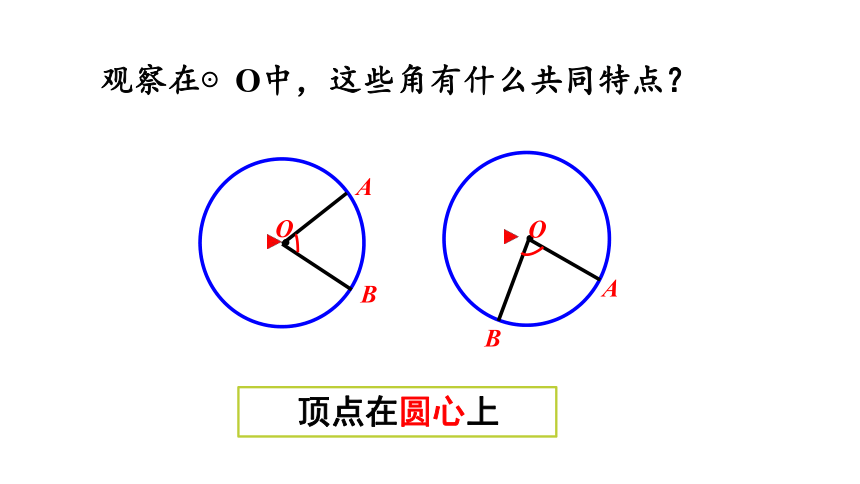
观察在⊙O中,这些角有什么共同特点?
顶点在圆心上
O
A
B
M
1.
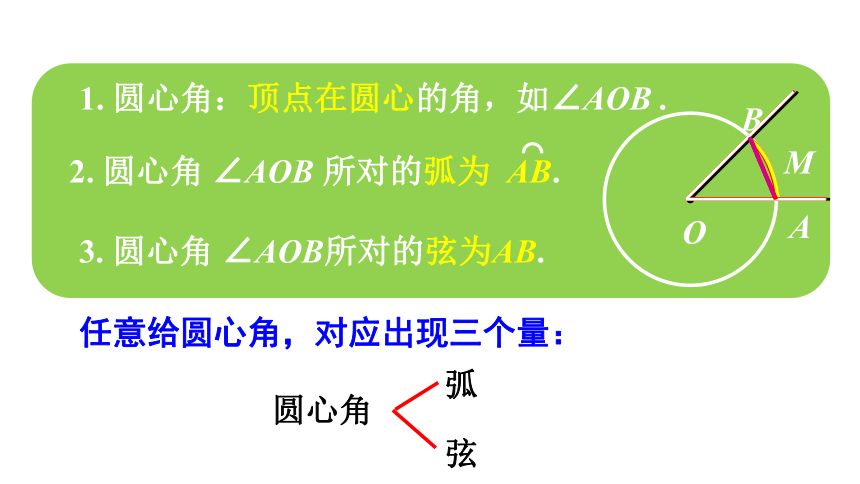
圆心角:顶点在圆心的角,如∠AOB
.
3.
圆心角
∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.
圆心角
∠AOB
所对的弧为
AB.
⌒
弦
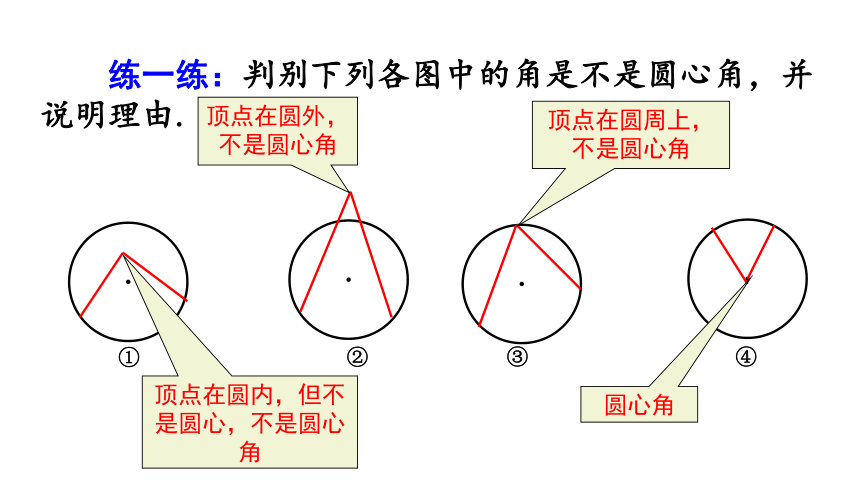
练一练:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
顶点在圆内,但不是圆心,不是圆心角
顶点在圆外,不是圆心角
顶点在圆周上,不是圆心角
圆心角
∠AOB=∠A′OB′
·
O
A
B
A′
B′
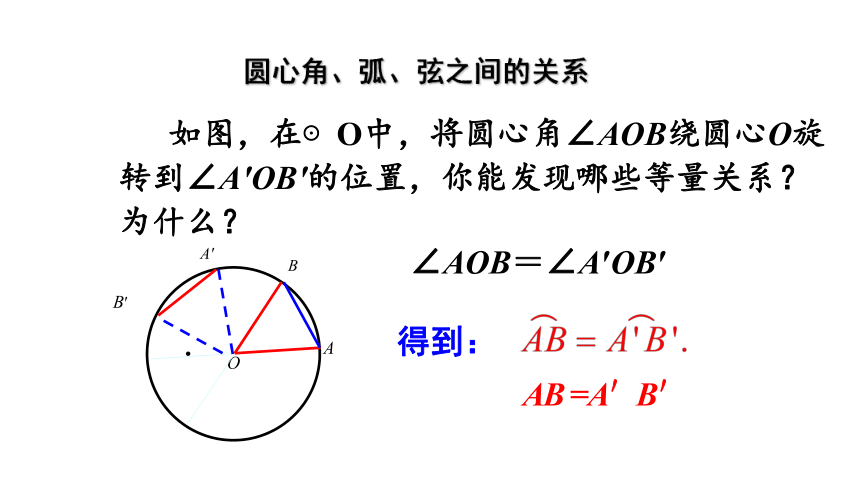
如图,在⊙O中,将圆心角∠AOB绕圆心O旋转到∠A'OB'的位置,你能发现哪些等量关系?为什么?
得到:
AB
=A'B'
圆心角、弧、弦之间的关系
在⊙O中,如果∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,可得:
在⊙O中,如果∠AOB=
∠COD,
那么,
AB与CD
,弦AB=弦CD
在同圆中探究
⌒
⌒
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
O
′
C
D
通过平移和旋转将两个等圆变成同一个圆,可得:
如果∠AOB=∠COD,
那么,AB=CD,
弦AB=弦CD.
⌒
⌒
在等圆中探究
在同一个圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角的关系定理
【想一想】定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
在同一个圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
弧、弦与圆心角关系定理的推论
关系结构图
解:
∵BC=CD=DE
例1
如图,AB是⊙O
的直径,BC=CD=DE.
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
考点探究1
利用弧、弦、圆心角的关系求角度
⌒
⌒
⌒
⌒
⌒
⌒
×
×
(1)等弦所对的弧相等.
(
)
(2)等弧所对的弦相等.
(
)
(3)圆心角相等,所对的弦相等.
(
)
×
1.
判断正误。
巩固练习
证明:
∴
AB=AC.△ABC是等腰三角形.
又∵
∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
例2
如图,在⊙O中,
AB=AC
,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒
⌒
∵AB=CD,
⌒
⌒
考点探究2
利用弧、弦、圆心角的关系证明相等
探究新知
2.
填一填.
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,
_______________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB=
∠COD
∠AOB=
∠COD
AB=CD
(
(
AB=CD
(
(
巩固练习
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
解:OE=OF.
1.如果两个圆心角相等,那么
(
)
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
课堂检测
2.弦长等于半径的弦所对的圆心角等于
.
60
°
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是(
)
⌒
⌒
A
A.
AB=2CD
⌒
⌒
B.
AB>CD
⌒
⌒
C.
AB⌒
⌒
D.
不能确定
4.如图,已知AB、CD为⊙O的两条弦,AD=BC
求证:AB=CD.
.
C
A
B
D
O
⌒
⌒
⌒
⌒
AD=BC
∵
5.如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒
⌒
解:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,所以
AB=CE=DE
.
CE+DE=2AB,在△CDE中,CE+DE>CD,即CD<2AB.
⌒
⌒
A
B
C
E
O
易错点拨:在同圆或等圆中,由弧相等可推出对应的弦相等;但当弧有倍数关系时,弦不具备此关系.
⌒
⌒
⌒
⌒
D
24.1
圆的有关性质
24.1.3
弧、弦、圆心角
人教版数学九年级上册
3.
理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
1.
理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.
探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
学习目标
【思考】
圆是中心对称图形吗?它的对称中心在哪里?
·
圆心角的概念
探究新知
圆是中心对称图形
.
O
A
B
180°
【观察】1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
·
O
B
A
·
O
B
A
观察在⊙O中,这些角有什么共同特点?
顶点在圆心上
O
A
B
M
1.
圆心角:顶点在圆心的角,如∠AOB
.
3.
圆心角
∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.
圆心角
∠AOB
所对的弧为
AB.
⌒
弦
练一练:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
顶点在圆内,但不是圆心,不是圆心角
顶点在圆外,不是圆心角
顶点在圆周上,不是圆心角
圆心角
∠AOB=∠A′OB′
·
O
A
B
A′
B′
如图,在⊙O中,将圆心角∠AOB绕圆心O旋转到∠A'OB'的位置,你能发现哪些等量关系?为什么?
得到:
AB
=A'B'
圆心角、弧、弦之间的关系
在⊙O中,如果∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,可得:
在⊙O中,如果∠AOB=
∠COD,
那么,
AB与CD
,弦AB=弦CD
在同圆中探究
⌒
⌒
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
O
′
C
D
通过平移和旋转将两个等圆变成同一个圆,可得:
如果∠AOB=∠COD,
那么,AB=CD,
弦AB=弦CD.
⌒
⌒
在等圆中探究
在同一个圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
弧、弦与圆心角的关系定理
【想一想】定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
在同一个圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
弧、弦与圆心角关系定理的推论
关系结构图
解:
∵BC=CD=DE
例1
如图,AB是⊙O
的直径,BC=CD=DE.
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
考点探究1
利用弧、弦、圆心角的关系求角度
⌒
⌒
⌒
⌒
⌒
⌒
×
×
(1)等弦所对的弧相等.
(
)
(2)等弧所对的弦相等.
(
)
(3)圆心角相等,所对的弦相等.
(
)
×
1.
判断正误。
巩固练习
证明:
∴
AB=AC.△ABC是等腰三角形.
又∵
∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
例2
如图,在⊙O中,
AB=AC
,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒
⌒
∵AB=CD,
⌒
⌒
考点探究2
利用弧、弦、圆心角的关系证明相等
探究新知
2.
填一填.
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,
_______________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB=
∠COD
∠AOB=
∠COD
AB=CD
(
(
AB=CD
(
(
巩固练习
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
解:OE=OF.
1.如果两个圆心角相等,那么
(
)
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
课堂检测
2.弦长等于半径的弦所对的圆心角等于
.
60
°
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是(
)
⌒
⌒
A
A.
AB=2CD
⌒
⌒
B.
AB>CD
⌒
⌒
C.
AB
⌒
D.
不能确定
4.如图,已知AB、CD为⊙O的两条弦,AD=BC
求证:AB=CD.
.
C
A
B
D
O
⌒
⌒
⌒
⌒
AD=BC
∵
5.如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒
⌒
解:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,所以
AB=CE=DE
.
CE+DE=2AB,在△CDE中,CE+DE>CD,即CD<2AB.
⌒
⌒
A
B
C
E
O
易错点拨:在同圆或等圆中,由弧相等可推出对应的弦相等;但当弧有倍数关系时,弦不具备此关系.
⌒
⌒
⌒
⌒
D
同课章节目录
