鲁教版(五四制)七年级上册数学第五章位置和坐标单元测试(含解析)
文档属性
| 名称 | 鲁教版(五四制)七年级上册数学第五章位置和坐标单元测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 00:00:00 | ||
图片预览




文档简介
第五章-位置与坐标
一、单选题
1.在平面直角坐标系中,点P(-3,2)所在象限为
(????
)
A.?第一象限????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
2.如果点P(m+3,m+1)在直角坐标系的x轴上,P点坐标为(?????
)
A.?(0,-2)??????????????????????????????B.?(2,0)??????????????????????????????C.?(4,0)??????????????????????????????D.?(0,-4)
3.在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.?(7,-500)???????????????????B.?(-3,400)???????????????????C.?(9,600)???????????????????D.?(-2,-800)
4.已知M(0,2)关于x轴对称的点为N,线段MN的中点坐标是(
???)
A.?(0,-2)????????????????????????B.?(0,0)????????????????????????C.?(-2,0)????????????????????????D.?(0,4)
5.已知点A(-1,0)点B(2,0),在y轴上存在点C,使三角形ABC的面积为6,则点C的坐标是(
??)
A.?(0,4)????????????????????B.?(0,2)????????????????????C.?(0,2)或(0,-2)????????????????????D.?(0,4)或(0,-4)
6.下列两点是关于x轴对称的是(????
)
A.?(-1,3)和(1,-3)???????????B.?(3,-5)和(-3,-5)???????????C.?(-2,4)和(2,-4)???????????D.?(5,-3)和(5,3)
7.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为(?????
)
A.?(-1,)???????????????????????B.?(0,)???????????????????????C.?(,0)???????????????????????D.?(1,)
8.在平面直角坐标系中,点
(-3,5)关于x轴的对称点的坐标是(??
)
A.?(3,5)??????????????????????????????B.?(3,-5)??????????????????????????????C.?(5,-3)??????????????????????????????D.?(-3,-5)
9.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
(?
)
A.?(3,2)??????????????????????????B.?(3,1)??????????????????????????C.?(2,2)??????????????????????????D.?(-2,2)
二、填空题
10.数学活动中.张明和王丽向老师说明他们的位置(单位:m).
张明:我这里的坐标是(﹣200,300);
王丽:我这里的坐标是(300,300).
则老师知道张明与王丽之间的距离是________m.
11.如图,象棋盘上,若“将”位于点(1,-1),“车”位于点(-3,-1),则“马”位于点________.
12.下列说法中:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;④甲地距乙地2
km,其中能确定位置的有________个.
13.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2
,
点A2的伴随点为A3
,
点A3的伴随点为A4
,
…,这样依次得到点A1
,
A2
,
A3
,
…,An
,
….若点A1的坐标为(3,1),则点A2015的坐标为________;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为________。
14.己知点A与B关于x轴对称,若点A坐标为(-3,1),则点B的坐标为________.
15.已知点P(3,m)关于x轴的对称点为Q(n,2),则2n﹣m=________.
16.点P关于x轴对称的点是(3,﹣4),则点P关于y轴对称的点的坐标是________.
17.把边长为2的正方形OABC放在如图所示的平面直角坐标系中,则点B的坐标为________.
三、解答题
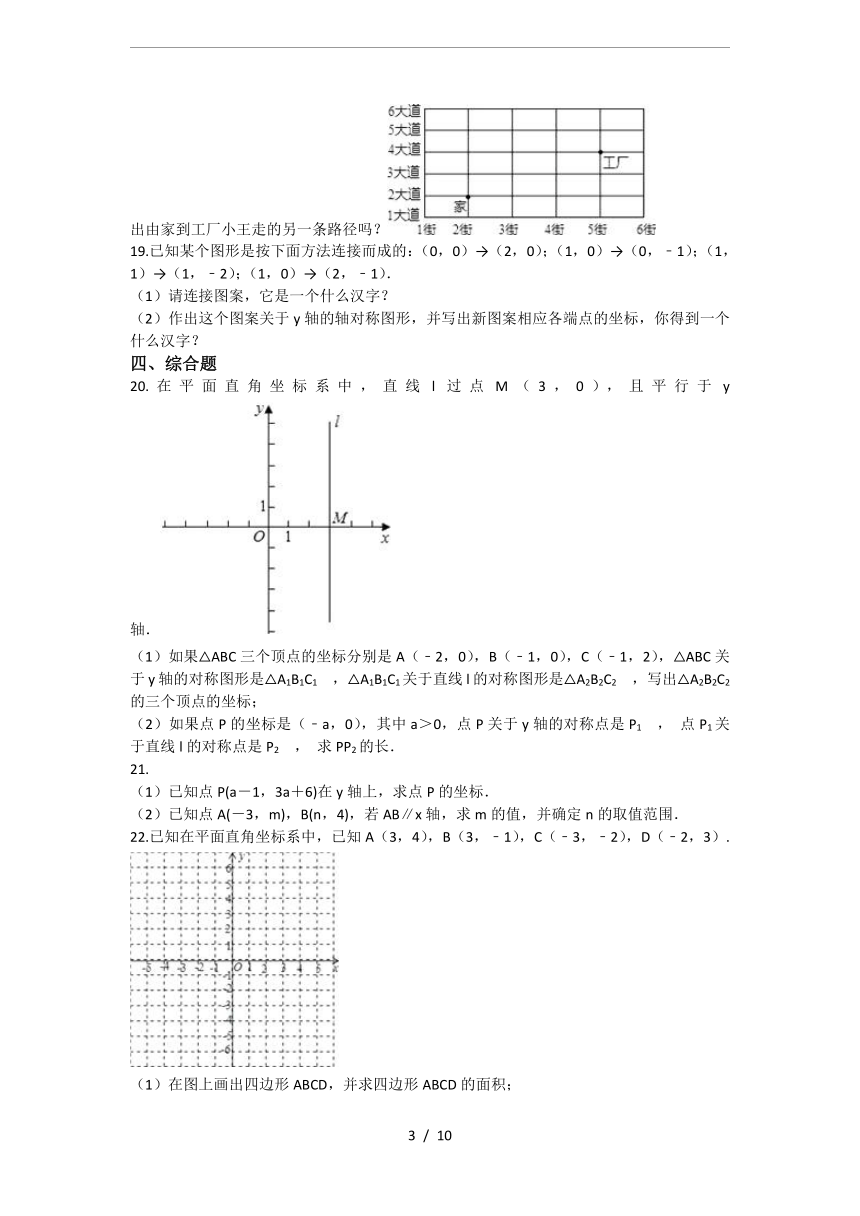
18.如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
19.已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
四、综合题
20.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1
,
△A1B1C1关于直线l的对称图形是△A2B2C2
,
写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1
,
点P1关于直线l的对称点是P2
,
求PP2的长.
21.??????????
(1)已知点P(a-1,3a+6)在y轴上,求点P的坐标.
(2)已知点A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的取值范围.
22.已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3).
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
答案
一、单选题
1.【答案】
B
【解析】【分析】根据点在第二象限的坐标特点即可解答.
【解答】∵点的横坐标-3<0,纵坐标2>0,
∴这个点在第二象限.
故选B.
【点评】解决本题的关键是记住平面直角坐标系中各个象限内点的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
2.【答案】B
【解析】【分析】因为点P(m+3,m+1)在直角坐标系的x轴上,那么其纵坐标是0,即m+1=0,m=-1,进而可求得点P的横纵坐标.
【解答】∵点P(m+3,m+1)在直角坐标系的x轴上,
∴m+1=0,
∴m=-1,
把m=-1代入横坐标得:m+3=2.
则P点坐标为(2,0).
故选B.
【点评】本题主要考查了点在x轴上时纵坐标为0的特点,比较简单.
3.【答案】
A
【解析】【分析】根据第四象限中点的符号的特点可知目标的坐标可能是(7,-500).
【解答】因为目标在第四象限,所以其坐标的符号是(+,-),观察各选项只有B符合题意,故选A.
【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
4.【答案】
B
【解析】【解答】M(0,2)关于x轴对称的点为N,所以点N的坐标为(0,-2),所以线段MN的中点坐标是(0,0).
【分析】关于x轴对称的两点的坐标特点为横坐标相等,纵坐标互为相反数.
5.【答案】
D
【解析】【解答】根据题意,可利用S△ABC=6,
可知C点坐标可以在x轴上方或下方,
可得出C点坐标为
(0,4)或(0,-4)》
故答案为:D.
【分析】利用三角形的面积公式,结合直角坐标系,得到C点坐标。
6.【答案】D
【解析】【分析】根据点(x,y)关于轴对称的点的坐标为(x,-y),可知选项A、B、C均不符合题意,只有选项D正确,故选D.
7.【答案】
B
【解析】
【分析】连接OQ、OP,求出∠POQ的度数,得出等边三角形POQ,得出PQ=OQ=OP=2,∠OPQ=∠OQP=60°,求出∠AOQ度数,根据三角形的内角和定理求出∠QAO,求出AQ、OA,即可得出答案.
【解答】连接OQ、PO,
则∠POQ=120°-60°=60,
∵PO=OQ,
∴△POQ是等边三角形,
∴PQ=OP=OQ=
×4cm=2cm,∠OPQ=∠OQP=60°,
∵∠AOQ=90°-60°=30°,
∴∠QAO=180°-60°-30°=90°,
∴AQ=OQ=2cm,
∵在Rt△AOQ中,由勾股定理得:OA=,
∴A的坐标是(0,),
故选B.
8.【答案】D
【解析】【解答】∵点P(-3,5)关于x轴的对称,∴对应点的横坐标为-3,纵坐标为-5,∴点P(-3,5)关于x轴对称点的坐标为(-3,-5).
故答案为:D.
【分析】点(X,Y)关于X轴的对称点为(X,-Y),故点P(-3,5)关于x轴对称点的坐标为(-3,-5)
9.【答案】
A
【解析】
【分析】先根据棋子“车”的坐标画出直角坐标系,然后写出棋子“炮”的坐标.
【解答】棋子“炮”的坐标为(3,2).
故选A.
【点评】本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征
二、填空题
10.【答案】500
【解析】【解答】解:∵张明的坐标是(﹣200,300),王丽的坐标是(300,300),
∴两人之间的距离为300﹣(﹣200)=300+200=500.
故答案为:500.
【分析】根据纵坐标相等,两人之间的距离等于横坐标的差解答.
11.【答案】
(4,2)
【解析】【解答】建立直角坐标系,
可得到马的坐标为(4,2)
【分析】根据题意,可建立直角坐标系,写出马的坐标即可。
12.【答案】3
【解析】【解答】解:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;可以准确的表示出位置,而④甲地距乙地2
km却不能确定甲地在乙地什么方向上距乙2km,所以不能确定位置,所以能确定位置的有3个.【分析】用坐标确定位置:一定要知道其横坐标和纵坐标,由此即可得出答案.
13.【答案】(-4,-3);-1<a<1且0<b<2
【解析】【解答】∵A1的坐标为(4,5),
∴A2(-4,5),A3(-4,-3),A4(4,-3),A5(4,5),
…,
依此类推,每4个点为一个循环组依次循环,
∵2015÷4=503余3,
∴点A2015的坐标与A3的坐标相同,为(-4,-3);
∵点A1的坐标为(a,b),
∴A2(-b+1,a+1),A3(-a,-b+2),A4(b-1,-a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴
,
,
解得-1<a<1,0<b<2.
故答案为:(-4,-3);-1<a<1且0<b<2.
【分析】考察平面直角坐标系内点的坐标特征.理解平面直角坐标系内点的坐标特征.
14.【答案】
(-3,-l)
【解析】【解答】解:
己知点A与B关于x轴对称,若点A坐标为(-3,1)
∴点B的坐标为:
(-3,-1)
故答案为:
(-3,-1)
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,就可得到点B的坐标。
15.【答案】8
【解析】【解答】解:∵点P(3,m)关于x轴的对称点Q的坐标是(n,2),
∴m=﹣2,n=3,
∴2n﹣m=8,
故答案为:8.
【分析】关于x轴对称的点坐标特点是“横同纵反”.
16.【答案】(﹣3,4)
【解析】【解答】解:∵点P关于x轴对称的点是(3,﹣4),则P点的坐标是(3,4).
∴点P关于y轴对称的点的坐标是(﹣3,4).
故答案为:(﹣3,4).
【分析】根据两点关于x轴对称,即横坐标相等,纵坐标为相反数;关于y轴对称,即横坐标为相反数,纵坐标相等,求出坐标。
17.【答案】
(2,﹣2)
【解析】【解答】解:∵边长为2的正方形OABC,
∴OC=OA=2,
∴点B的坐标为(2,﹣2),
故答案为:(2,﹣2),
【分析】根据正方形的性质可得OC=OA=2,从而得出B的坐标.
三、解答题
18.【答案】解:∵(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的路径∴小王家的位置为(2,2),工厂的位置为(5,4).
故答案为(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
【解析】【分析】由图和平面直角坐标系的特征可知,小王家的位置为(2,2),工厂的位置为(5,4),则另一条的路径即可解。
19.【答案】(1)解:如图所示:这是一个“木”字;
(2)解:如图所示:这是一个“林”字;
对应各端点坐标如下:
(0,0)→(-2,0);(-1,0)→(0,-1);(-1,1)→(-1,-2);(-1,0)→(-2,-1).
【解析】【分析】(1)根据题中点的坐标,在坐标系中描点并连点即可。
(2)图案关于y轴对称,同时,点的坐标也关于y轴对称,根据4个象限横、纵坐标的特点,即可得出新图案相应各端点的坐标。
四、综合题
20.【答案】(1)解:△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
(2)解:如图1,当0<a≤3时,∵P与P1关于y轴对称,P(-a,0),∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:
=3,即x=6-a,
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与P1关于y轴对称,P(-a,0),∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:
=3,即x=6-a,
∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
【解析】【分析】(1)直线l平行于y轴,关于y轴对称点的坐标特点是纵坐标不变,横坐标互为相反数;关于直线l的对称的图形,由点M的坐标得到纵坐标不变,横坐标都加6;(2)点P关于y轴的对称点是P1
,
点P1关于直线l的对称点是P2
,
由(1)求出P2的坐标,得到PP2的长.
21.【答案】(1)解:∵点P(a-1,3a+6)在y轴上,
∴横坐标为0,即a-1=0,∴a=1.
∴点P的坐标为(0,9)
(2)解:∵AB∥x轴,
∴点A(-3,m),B(n,4)的纵坐标相等,
∴m=4.
∵AB∥x轴,点B的坐标为(n,4),
∴A,B两点不能重合,
∴n
的取值范围为n≠-3
【解析】【分析】(1)根据在y轴上点的坐标是横坐标=0,得到a-1=0,求出点P的坐标;(2)由AB∥x轴得到点A、B的纵坐标相等,求出m的值;由A,B两点不能重合,得到n的取值范围.
22.【答案】(1)解:如图所示.
S四边形ABCD=6×6﹣
×6×1﹣
×5×1﹣
×5×1﹣1
=36﹣3﹣
﹣
﹣1
=36﹣3﹣5﹣1
=27
(2)解:∵P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),
∴平移后各点横坐标加3,纵坐标减3,
∴平移后的点坐标A(6,1),B(6,﹣4),C(0,﹣5),D(1,0).
【解析】【分析】第一问求四边形面积,用大的正方形的面积减去三个直角三角形的和一个小正方形的面积,即可.
第二问通过点P的平移,再找出平移后的A、B、C、D四个顶点的坐标.
/
一、单选题
1.在平面直角坐标系中,点P(-3,2)所在象限为
(????
)
A.?第一象限????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
2.如果点P(m+3,m+1)在直角坐标系的x轴上,P点坐标为(?????
)
A.?(0,-2)??????????????????????????????B.?(2,0)??????????????????????????????C.?(4,0)??????????????????????????????D.?(0,-4)
3.在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.?(7,-500)???????????????????B.?(-3,400)???????????????????C.?(9,600)???????????????????D.?(-2,-800)
4.已知M(0,2)关于x轴对称的点为N,线段MN的中点坐标是(
???)
A.?(0,-2)????????????????????????B.?(0,0)????????????????????????C.?(-2,0)????????????????????????D.?(0,4)
5.已知点A(-1,0)点B(2,0),在y轴上存在点C,使三角形ABC的面积为6,则点C的坐标是(
??)
A.?(0,4)????????????????????B.?(0,2)????????????????????C.?(0,2)或(0,-2)????????????????????D.?(0,4)或(0,-4)
6.下列两点是关于x轴对称的是(????
)
A.?(-1,3)和(1,-3)???????????B.?(3,-5)和(-3,-5)???????????C.?(-2,4)和(2,-4)???????????D.?(5,-3)和(5,3)
7.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为(?????
)
A.?(-1,)???????????????????????B.?(0,)???????????????????????C.?(,0)???????????????????????D.?(1,)
8.在平面直角坐标系中,点
(-3,5)关于x轴的对称点的坐标是(??
)
A.?(3,5)??????????????????????????????B.?(3,-5)??????????????????????????????C.?(5,-3)??????????????????????????????D.?(-3,-5)
9.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
(?
)
A.?(3,2)??????????????????????????B.?(3,1)??????????????????????????C.?(2,2)??????????????????????????D.?(-2,2)
二、填空题
10.数学活动中.张明和王丽向老师说明他们的位置(单位:m).
张明:我这里的坐标是(﹣200,300);
王丽:我这里的坐标是(300,300).
则老师知道张明与王丽之间的距离是________m.
11.如图,象棋盘上,若“将”位于点(1,-1),“车”位于点(-3,-1),则“马”位于点________.
12.下列说法中:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;④甲地距乙地2
km,其中能确定位置的有________个.
13.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2
,
点A2的伴随点为A3
,
点A3的伴随点为A4
,
…,这样依次得到点A1
,
A2
,
A3
,
…,An
,
….若点A1的坐标为(3,1),则点A2015的坐标为________;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为________。
14.己知点A与B关于x轴对称,若点A坐标为(-3,1),则点B的坐标为________.
15.已知点P(3,m)关于x轴的对称点为Q(n,2),则2n﹣m=________.
16.点P关于x轴对称的点是(3,﹣4),则点P关于y轴对称的点的坐标是________.
17.把边长为2的正方形OABC放在如图所示的平面直角坐标系中,则点B的坐标为________.
三、解答题
18.如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
19.已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
四、综合题
20.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1
,
△A1B1C1关于直线l的对称图形是△A2B2C2
,
写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1
,
点P1关于直线l的对称点是P2
,
求PP2的长.
21.??????????
(1)已知点P(a-1,3a+6)在y轴上,求点P的坐标.
(2)已知点A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的取值范围.
22.已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3).
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
答案
一、单选题
1.【答案】
B
【解析】【分析】根据点在第二象限的坐标特点即可解答.
【解答】∵点的横坐标-3<0,纵坐标2>0,
∴这个点在第二象限.
故选B.
【点评】解决本题的关键是记住平面直角坐标系中各个象限内点的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
2.【答案】B
【解析】【分析】因为点P(m+3,m+1)在直角坐标系的x轴上,那么其纵坐标是0,即m+1=0,m=-1,进而可求得点P的横纵坐标.
【解答】∵点P(m+3,m+1)在直角坐标系的x轴上,
∴m+1=0,
∴m=-1,
把m=-1代入横坐标得:m+3=2.
则P点坐标为(2,0).
故选B.
【点评】本题主要考查了点在x轴上时纵坐标为0的特点,比较简单.
3.【答案】
A
【解析】【分析】根据第四象限中点的符号的特点可知目标的坐标可能是(7,-500).
【解答】因为目标在第四象限,所以其坐标的符号是(+,-),观察各选项只有B符合题意,故选A.
【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
4.【答案】
B
【解析】【解答】M(0,2)关于x轴对称的点为N,所以点N的坐标为(0,-2),所以线段MN的中点坐标是(0,0).
【分析】关于x轴对称的两点的坐标特点为横坐标相等,纵坐标互为相反数.
5.【答案】
D
【解析】【解答】根据题意,可利用S△ABC=6,
可知C点坐标可以在x轴上方或下方,
可得出C点坐标为
(0,4)或(0,-4)》
故答案为:D.
【分析】利用三角形的面积公式,结合直角坐标系,得到C点坐标。
6.【答案】D
【解析】【分析】根据点(x,y)关于轴对称的点的坐标为(x,-y),可知选项A、B、C均不符合题意,只有选项D正确,故选D.
7.【答案】
B
【解析】
【分析】连接OQ、OP,求出∠POQ的度数,得出等边三角形POQ,得出PQ=OQ=OP=2,∠OPQ=∠OQP=60°,求出∠AOQ度数,根据三角形的内角和定理求出∠QAO,求出AQ、OA,即可得出答案.
【解答】连接OQ、PO,
则∠POQ=120°-60°=60,
∵PO=OQ,
∴△POQ是等边三角形,
∴PQ=OP=OQ=
×4cm=2cm,∠OPQ=∠OQP=60°,
∵∠AOQ=90°-60°=30°,
∴∠QAO=180°-60°-30°=90°,
∴AQ=OQ=2cm,
∵在Rt△AOQ中,由勾股定理得:OA=,
∴A的坐标是(0,),
故选B.
8.【答案】D
【解析】【解答】∵点P(-3,5)关于x轴的对称,∴对应点的横坐标为-3,纵坐标为-5,∴点P(-3,5)关于x轴对称点的坐标为(-3,-5).
故答案为:D.
【分析】点(X,Y)关于X轴的对称点为(X,-Y),故点P(-3,5)关于x轴对称点的坐标为(-3,-5)
9.【答案】
A
【解析】
【分析】先根据棋子“车”的坐标画出直角坐标系,然后写出棋子“炮”的坐标.
【解答】棋子“炮”的坐标为(3,2).
故选A.
【点评】本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征
二、填空题
10.【答案】500
【解析】【解答】解:∵张明的坐标是(﹣200,300),王丽的坐标是(300,300),
∴两人之间的距离为300﹣(﹣200)=300+200=500.
故答案为:500.
【分析】根据纵坐标相等,两人之间的距离等于横坐标的差解答.
11.【答案】
(4,2)
【解析】【解答】建立直角坐标系,
可得到马的坐标为(4,2)
【分析】根据题意,可建立直角坐标系,写出马的坐标即可。
12.【答案】3
【解析】【解答】解:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;可以准确的表示出位置,而④甲地距乙地2
km却不能确定甲地在乙地什么方向上距乙2km,所以不能确定位置,所以能确定位置的有3个.【分析】用坐标确定位置:一定要知道其横坐标和纵坐标,由此即可得出答案.
13.【答案】(-4,-3);-1<a<1且0<b<2
【解析】【解答】∵A1的坐标为(4,5),
∴A2(-4,5),A3(-4,-3),A4(4,-3),A5(4,5),
…,
依此类推,每4个点为一个循环组依次循环,
∵2015÷4=503余3,
∴点A2015的坐标与A3的坐标相同,为(-4,-3);
∵点A1的坐标为(a,b),
∴A2(-b+1,a+1),A3(-a,-b+2),A4(b-1,-a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴
,
,
解得-1<a<1,0<b<2.
故答案为:(-4,-3);-1<a<1且0<b<2.
【分析】考察平面直角坐标系内点的坐标特征.理解平面直角坐标系内点的坐标特征.
14.【答案】
(-3,-l)
【解析】【解答】解:
己知点A与B关于x轴对称,若点A坐标为(-3,1)
∴点B的坐标为:
(-3,-1)
故答案为:
(-3,-1)
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,就可得到点B的坐标。
15.【答案】8
【解析】【解答】解:∵点P(3,m)关于x轴的对称点Q的坐标是(n,2),
∴m=﹣2,n=3,
∴2n﹣m=8,
故答案为:8.
【分析】关于x轴对称的点坐标特点是“横同纵反”.
16.【答案】(﹣3,4)
【解析】【解答】解:∵点P关于x轴对称的点是(3,﹣4),则P点的坐标是(3,4).
∴点P关于y轴对称的点的坐标是(﹣3,4).
故答案为:(﹣3,4).
【分析】根据两点关于x轴对称,即横坐标相等,纵坐标为相反数;关于y轴对称,即横坐标为相反数,纵坐标相等,求出坐标。
17.【答案】
(2,﹣2)
【解析】【解答】解:∵边长为2的正方形OABC,
∴OC=OA=2,
∴点B的坐标为(2,﹣2),
故答案为:(2,﹣2),
【分析】根据正方形的性质可得OC=OA=2,从而得出B的坐标.
三、解答题
18.【答案】解:∵(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的路径∴小王家的位置为(2,2),工厂的位置为(5,4).
故答案为(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
【解析】【分析】由图和平面直角坐标系的特征可知,小王家的位置为(2,2),工厂的位置为(5,4),则另一条的路径即可解。
19.【答案】(1)解:如图所示:这是一个“木”字;
(2)解:如图所示:这是一个“林”字;
对应各端点坐标如下:
(0,0)→(-2,0);(-1,0)→(0,-1);(-1,1)→(-1,-2);(-1,0)→(-2,-1).
【解析】【分析】(1)根据题中点的坐标,在坐标系中描点并连点即可。
(2)图案关于y轴对称,同时,点的坐标也关于y轴对称,根据4个象限横、纵坐标的特点,即可得出新图案相应各端点的坐标。
四、综合题
20.【答案】(1)解:△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
(2)解:如图1,当0<a≤3时,∵P与P1关于y轴对称,P(-a,0),∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:
=3,即x=6-a,
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与P1关于y轴对称,P(-a,0),∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得:
=3,即x=6-a,
∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
【解析】【分析】(1)直线l平行于y轴,关于y轴对称点的坐标特点是纵坐标不变,横坐标互为相反数;关于直线l的对称的图形,由点M的坐标得到纵坐标不变,横坐标都加6;(2)点P关于y轴的对称点是P1
,
点P1关于直线l的对称点是P2
,
由(1)求出P2的坐标,得到PP2的长.
21.【答案】(1)解:∵点P(a-1,3a+6)在y轴上,
∴横坐标为0,即a-1=0,∴a=1.
∴点P的坐标为(0,9)
(2)解:∵AB∥x轴,
∴点A(-3,m),B(n,4)的纵坐标相等,
∴m=4.
∵AB∥x轴,点B的坐标为(n,4),
∴A,B两点不能重合,
∴n
的取值范围为n≠-3
【解析】【分析】(1)根据在y轴上点的坐标是横坐标=0,得到a-1=0,求出点P的坐标;(2)由AB∥x轴得到点A、B的纵坐标相等,求出m的值;由A,B两点不能重合,得到n的取值范围.
22.【答案】(1)解:如图所示.
S四边形ABCD=6×6﹣
×6×1﹣
×5×1﹣
×5×1﹣1
=36﹣3﹣
﹣
﹣1
=36﹣3﹣5﹣1
=27
(2)解:∵P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),
∴平移后各点横坐标加3,纵坐标减3,
∴平移后的点坐标A(6,1),B(6,﹣4),C(0,﹣5),D(1,0).
【解析】【分析】第一问求四边形面积,用大的正方形的面积减去三个直角三角形的和一个小正方形的面积,即可.
第二问通过点P的平移,再找出平移后的A、B、C、D四个顶点的坐标.
/
