小学数学北师大版五年级下包装的学问课件(14张ppt)
文档属性
| 名称 | 小学数学北师大版五年级下包装的学问课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 14:03:19 | ||
图片预览


文档简介
(共14张PPT)
包装的学问
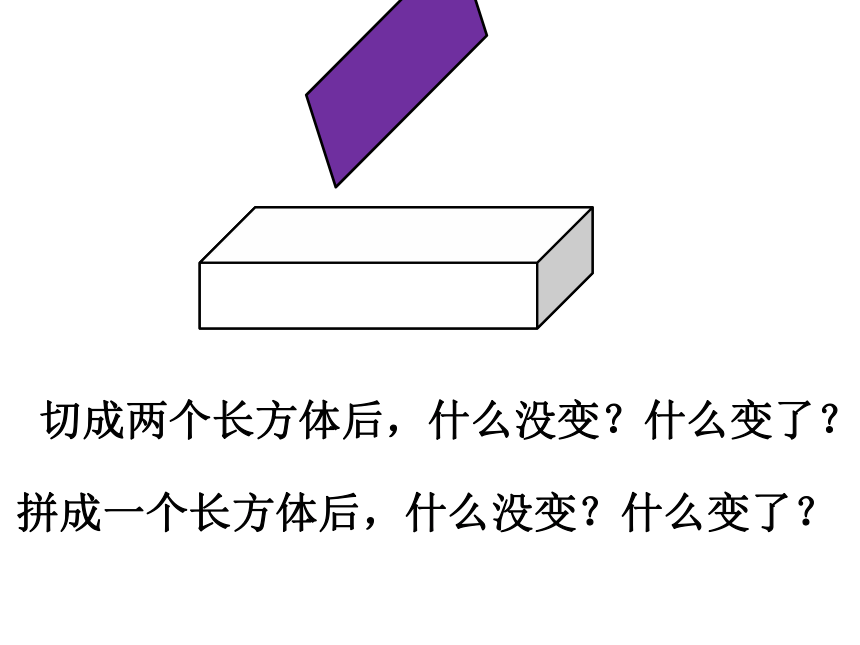
切成两个长方体后,什么没变?什么变了?
拼成一个长方体后,什么没变?什么变了?
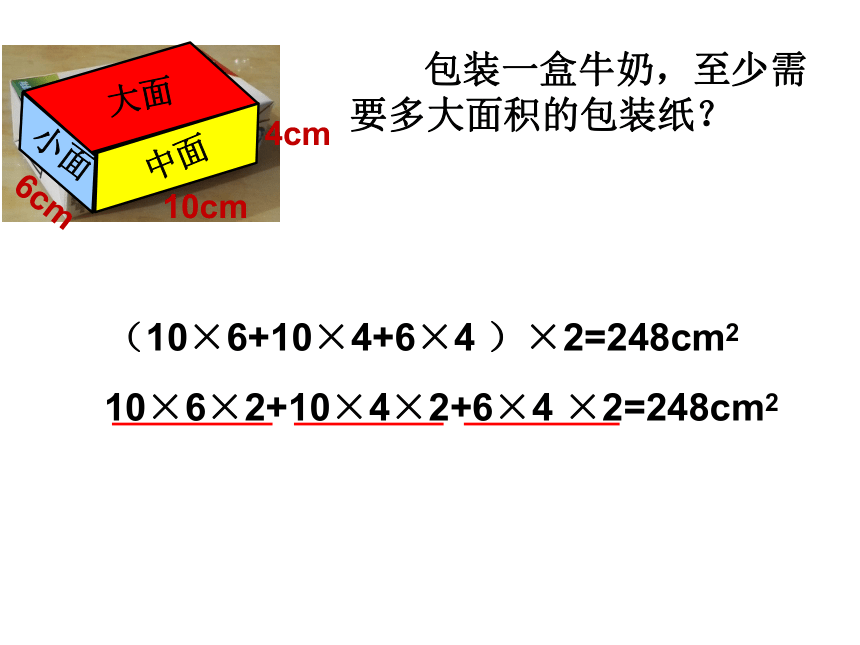
10cm
6cm
4cm
包装一盒牛奶,至少需要多大面积的包装纸?
(10×6+10×4+6×4
)×2=248cm2
10×6×2+10×4×2+6×4
×2=248cm2
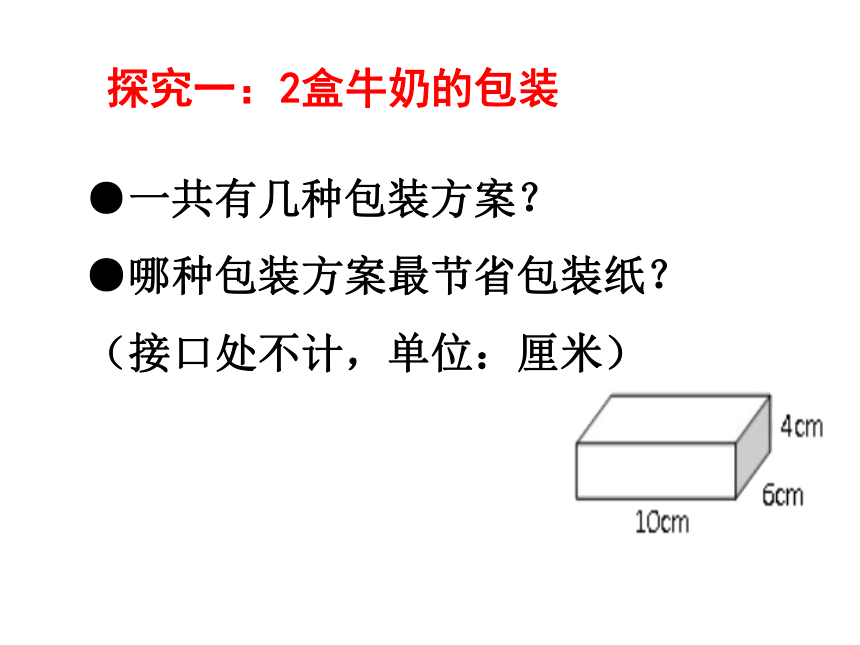
●一共有几种包装方案?
●哪种包装方案最节省包装纸?
(接口处不计,单位:厘米)
探究一:2盒牛奶的包装
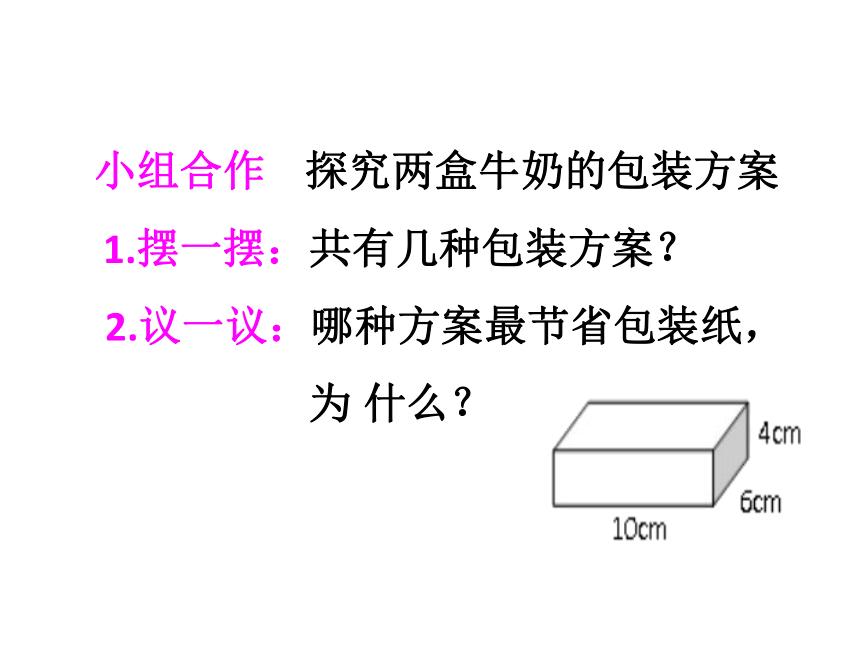
小组合作
探究两盒牛奶的包装方案
1.摆一摆:共有几种包装方案?
2.议一议:哪种方案最节省包装纸,
为
什么?
怎样包装最节省包装纸?
(接口处不计,单位:厘米)
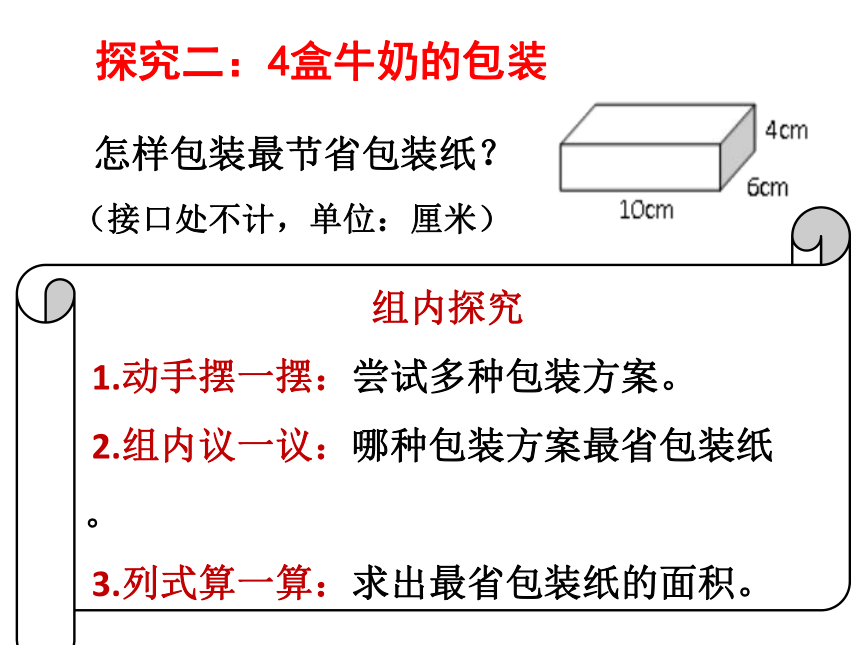
探究二:4盒牛奶的包装
组内探究
1.动手摆一摆:尝试多种包装方案。
2.组内议一议:哪种包装方案最省包装纸。
3.列式算一算:求出最省包装纸的面积。
6个大面
6个中面
6个小面
4大4中
4大4小
4中4小
你觉得哪种包装方案表面积最小?请阐述理由。
比一比:方案1和方案4哪个重叠面积多?
方案4最省包装纸
6个大面
4大4中
计算验证
(12×10+10×8+12×8)×2=592cm2
(6×10+10×16+6×16)×2=632cm2
答:方案4最节省包装纸。
592cm2
<
632cm2
6cm
10cm
4cm
4cm
4cm
4cm
6cm
10cm
4cm
4cm
6cm
观察思考:在总体积不变的情况下,长、宽、高与表面积大小有什么关系?
方案
长cm
宽cm
高cm
表面积cm2
③
40
6
4
848
②
24
10
4
752
⑥
20
12
4
736
⑤
20
6
8
656
①
10
6
16
632
④
10
12
8
592
你发现了吗?
同样体积的物体,包装的长、宽、高越(
),表面积越(
)。
形象地说,包装得过扁、过高、过宽等,表面积相对较大。
接近
小
这节课你有什么收获?
包装6包纸巾,怎样包装最省包装纸?
(长7cm、宽5cm、高2cm)
包装的学问
切成两个长方体后,什么没变?什么变了?
拼成一个长方体后,什么没变?什么变了?
10cm
6cm
4cm
包装一盒牛奶,至少需要多大面积的包装纸?
(10×6+10×4+6×4
)×2=248cm2
10×6×2+10×4×2+6×4
×2=248cm2
●一共有几种包装方案?
●哪种包装方案最节省包装纸?
(接口处不计,单位:厘米)
探究一:2盒牛奶的包装
小组合作
探究两盒牛奶的包装方案
1.摆一摆:共有几种包装方案?
2.议一议:哪种方案最节省包装纸,
为
什么?
怎样包装最节省包装纸?
(接口处不计,单位:厘米)
探究二:4盒牛奶的包装
组内探究
1.动手摆一摆:尝试多种包装方案。
2.组内议一议:哪种包装方案最省包装纸。
3.列式算一算:求出最省包装纸的面积。
6个大面
6个中面
6个小面
4大4中
4大4小
4中4小
你觉得哪种包装方案表面积最小?请阐述理由。
比一比:方案1和方案4哪个重叠面积多?
方案4最省包装纸
6个大面
4大4中
计算验证
(12×10+10×8+12×8)×2=592cm2
(6×10+10×16+6×16)×2=632cm2
答:方案4最节省包装纸。
592cm2
<
632cm2
6cm
10cm
4cm
4cm
4cm
4cm
6cm
10cm
4cm
4cm
6cm
观察思考:在总体积不变的情况下,长、宽、高与表面积大小有什么关系?
方案
长cm
宽cm
高cm
表面积cm2
③
40
6
4
848
②
24
10
4
752
⑥
20
12
4
736
⑤
20
6
8
656
①
10
6
16
632
④
10
12
8
592
你发现了吗?
同样体积的物体,包装的长、宽、高越(
),表面积越(
)。
形象地说,包装得过扁、过高、过宽等,表面积相对较大。
接近
小
这节课你有什么收获?
包装6包纸巾,怎样包装最省包装纸?
(长7cm、宽5cm、高2cm)
