不等的性质第一课时

(共22张PPT)
重庆市江津区白沙中学 王婷
比赛规则
学生分为四组，分别以A，B，C，D表示，比赛以老师提出问题后，各组学生以举手回答的方式进行，以加分、扣分来衡量各组的表现情况，最后以得分最高者胜出，将给予胜出组一定的奖励，具体比赛规则如下：
加分：问题回答正确者，则该组加10分；若回答错误都，则该组 不得分，则由其他同学加以补充，补充正确者，则该组加5分；若全班都无法回答，由老师补充，老师得10分。
扣分：出现以下情况者将视为违规，违规者则该组扣5分
1、当有同学在回答问题时，其他同学给予“帮助”者，违规；
2、不遵守课堂纪律者，违规。
40
你能表述下面两个交通标志中的数字符号表示什么意义吗？
4m
汽车的速度不超过40km/h
汽车的高度低于4m
速度v≤40（千米/小时）
高度h<4（米）
1、什么是不等式？
定义：用不等号连接的式子叫做不等式。
“＞、＜、≥、≤、≠”
温故知新
2、什么是等式？
定义：用等号“=”连接的表示相等关系的式子叫
3、等式的基本性质有哪些？
性质1：等式的两边都加（或减）同一个数（或式
性质2：等式的两边都乘以（或除以）同一个不为
子），结果仍相等；
0的数，结果仍相等；
做等式。
1、用“>”或“<”填空:
（1）- 1<3 -1+2 3+2 -1-3 3-3
（2）10>5 10+5 5+5 10-2____5-2
（3） 5>3 5+a 3+a 5-a 3-a
2、从以上的练习中，你发现了什么？这个“发现”是正确的吗？
<
<
<
<
<
<
不等式基本性质1：不等式的两边加（或减）同一个数（或式子），
_________________
不等号的方向不变。
如果____,那么_________.
a>b
a±c>b±c
符号语言：
7÷5 ____ 3÷ 5 ,
（1）如果 7 ＞ 3，则：
7×5 ____ 3× 5 ,
＞
＞
（2）如果-1< 3,则：
-1×2____3×2,
-1÷2____3÷2,
<
<
你发现了什么
×3
÷3
(或 )
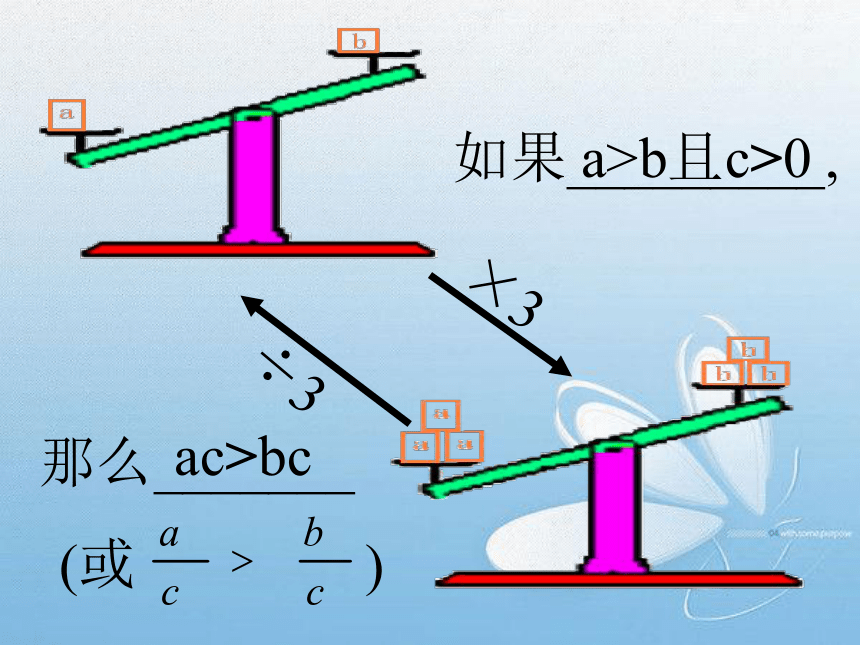
如果_________,
那么_______
a>b且c>0
ac>bc
（或 ）
不等式基本性质2：不等式的两边都乘以（或除以）同一个____，
不等号的方向____。
如果________,
a>b，c>0
ac>bc
不变
正数
符号语言：
那么
如果将性质2中的c>0，改成c<0,那性质2的结论还成立吗？
7 ×(-5)____3×(-5),
7 ÷ (-5)____3÷ (-5)
-1×(- 4)____3×( - 4),
-1÷ (- 4)____3÷ ( - 4)
如果 7 ＞ 3
如果-1< 3
不如行动
动
不等式基本性质3：不等式的两边都乘以（或除以）同一个____，
不等号的方向____。
负数
改变
如果________,
a>b，c<0
ac符号语言：
那么
（或 ）
不等式的三个基本性质
性质1： 如果a ＞b，那么a±c＞b±c.就是说，不等式两边都加上 (或减去）同一个数(或式子),不等号方向不变。
性质3：如果a>b，c<0 那么ac性质2：如果a ＞b，c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。
归纳性质
例1：判断下列各题的推导是否正确？为什么？
(1)因为7.5＞5.7，所以-7.5＜-5.7；
正确
答：
根据不等式基本性质3．
(2)因为a+8＞4，所以a＞-4；
正确
答：
根据不等式基本性质1
(3)因为4a＞4b，所以a＞b；
根据不等式基本性质2
正确
答：
当 a=0时，3a=2a．
当a＜0时，3a＜2a．(不等式基本性质3)
正确
答：
(4)因为-1＞-2，所以-a-1＞-a-2；
答：
根据不等式基本性质1．
(5)因为3＞2，所以3a＞2a．
错
应分情况逐一讨论．
当a＞0时，3a＞2a．(不等式基本性质2)
例2：将下列不等式化成x > a或 x < a 的形式
(1) x-5 > -1
(2) -2x > 4
(3) 7x < 6x －6
解:根据不等式的基本性质1,不等式两边都加上5得x > 4
解:根据不等式的基本性质3 , 不等式两边都除以-2得, x < －2
解:根据不等式的基本性质1,不等式两边都减去6x,得x < －6
1、 已知a＜0，用“＜”或“＞”号填空：
(1)a+2 ____2； (2)a-1 ____-1；
(3)3a____ 0； (4)-a/4____0;
(5)a2____0; (6)a3____0
(7)a-1____0； (8)|a|____0．
＜
＜
＜
＜
＜
＜
＜
＜
2、填空:
(1) ∵ 2a < 3a , ∴a是____数
(3) ∵ ax < a 且 x > 1 ,
∴a是____数
(2) ∵ , ∴a是____数
正
正
负
1、等式性质与不等式性质的不同之处；
2、在运用“不等式性质3”时应注意的问题.
P128：习题9.1第5、7题