5.3.1平行线的性质
图片预览



文档简介
(共19张PPT)
平行线 我们像是两条平行线 永远不能坦白面对面 我在你的左边 你在右边 没有交叉点 我们只是两条平行线 走多远都没有碰面的终点
我们像是两条平行线 永远不能坦白面对面 我在你的左边你在右边 没有交叉点 我们只是两条平行线 走多远都没有碰面的终点 而泪水只能含在心里面 我害怕模糊了视线
如图,
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b ( )
(3)∵ ∠2+∠4=____ (已知)
∴ a ∥ b ( )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180 °
同旁内角互补,两直线平行
c
B
F
E
D
C
B
A
P
P
8
7
6
5
4
3
2
1
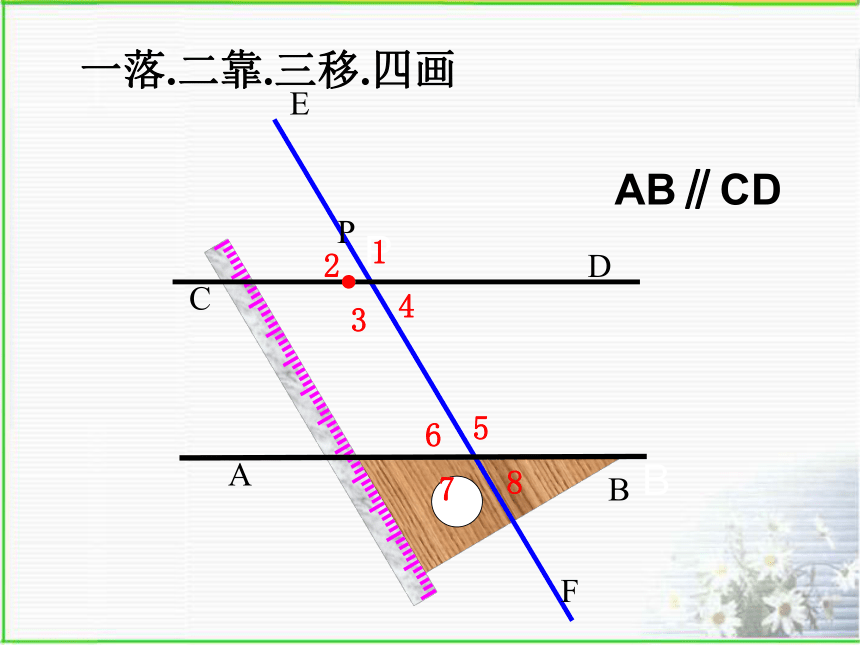
一落.二靠.三移.四画
AB∥CD
A
B
C
D
E
F
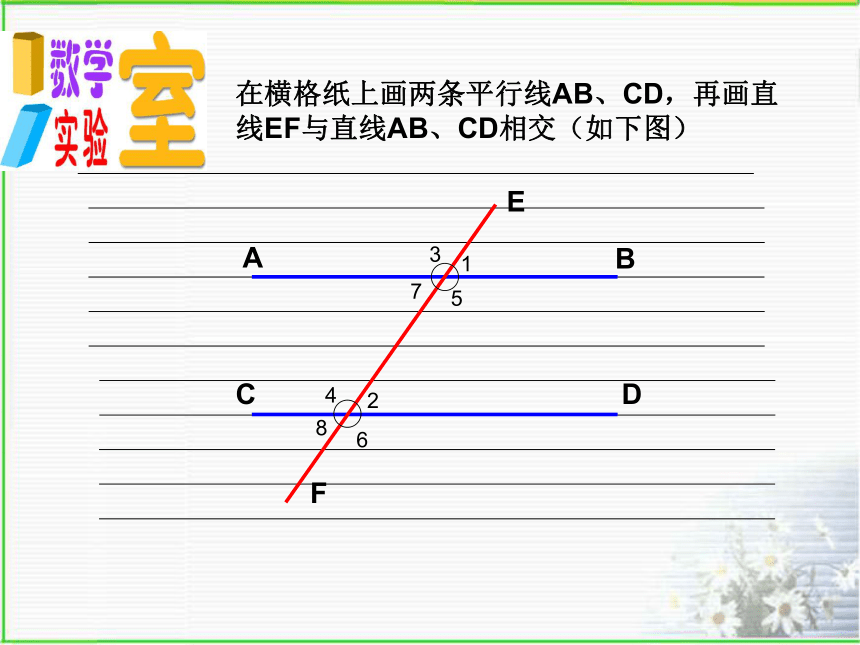
在横格纸上画两条平行线AB、CD,再画直线EF与直线AB、CD相交(如下图)
7
5
1
2
3
4
6
8
a
b
c
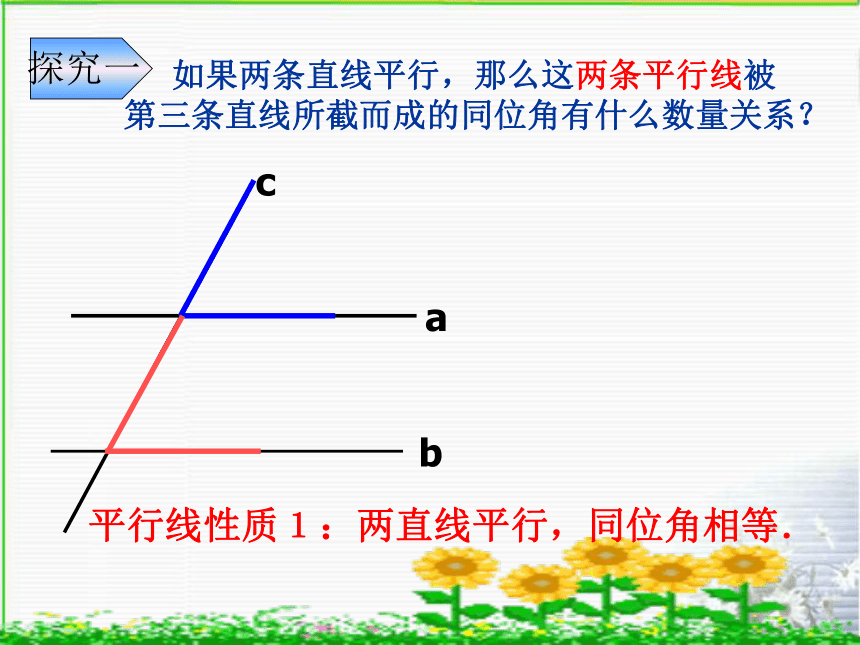
探究一
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
平行线性质1:两直线平行,同位角相等.
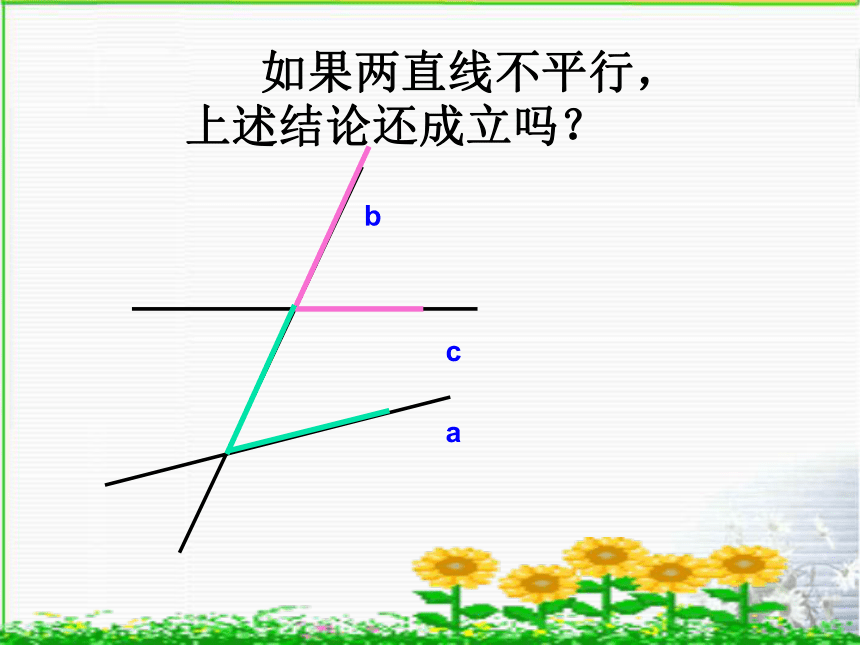
如果两直线不平行,
上述结论还成立吗?
b
c
a
已知:如图, a// b .
那么 3与 2有什么关系?
两直线平行,同位角相等
∠3
探究二
平行线性质2:两直线平行,内错角相等.
1
2
3
a
b
C
解: a∥b,
∠1=∠2
( )
又 ∠1= (对顶角相等),
∠ 2 = ∠3.(等量代换)
c
2
3
1
a
已知:如图a//b,
那么 2与 4有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 4=180°(邻补角定义)
2+ 4=180°(等量代换)
探究三
平行线性质3:两直线平行,同旁内角互补.
C
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵ a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补)
平行线的性质:
例题 如图是一块梯形铁片的残余部分,量得
∠A=115 °,∠D=100°,梯形另外两个角分别是
多少度
解:因为梯形上.下底互相平行,
所以
A
D
B
C
梯形的另外两个 角分别是
1.如图,直线a∥b, ∠1=54°,那么∠2, ∠3, ∠4各是多少度
解:
∵ ∠1 =54° (已知)
∴ ∠2=∠1 =54°(_____________)
∵ a∥b(已知)
∴ ∠4=∠1=54°(_______________________)
∠2+∠3=180°(_______________________)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
1
2
3
4
a
b
与
对顶角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证:(1)DE∥BC ;(2) ∠C的度数
a
b
内错角相等,两直线平行
∠4
两直线平行,同位角相等
∠5
3.填空(1)如图1∵∠1= ∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=180( )
a
b
c
d
1
2
3
4
5
图1
两直线平行,同旁内角互补
(2)如图2∵∠A+ ∠D=180(已知)
∴______∥______( )
∴∠B+∠C=_____( )
A
B
D
C
图2
AB
CD
同旁内角互补,两直线平行
1800
两直线平行,同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个性质:
平行线的三个判定:
1.如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
2.如图:已知 1= 2
求证: BCD+ D=180
BC
内错角相等,两直线平行
两直线平行,同旁内角互补
BC
证明:如图
∵ 1= 2(已知)
∴AD∥_____( )
∵AD ∥_____(已证)
∴ BCD+ D=180( )
作业:第23页3题.4题.
下课了
平行线 我们像是两条平行线 永远不能坦白面对面 我在你的左边 你在右边 没有交叉点 我们只是两条平行线 走多远都没有碰面的终点
我们像是两条平行线 永远不能坦白面对面 我在你的左边你在右边 没有交叉点 我们只是两条平行线 走多远都没有碰面的终点 而泪水只能含在心里面 我害怕模糊了视线
如图,
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b ( )
(3)∵ ∠2+∠4=____ (已知)
∴ a ∥ b ( )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180 °
同旁内角互补,两直线平行
c
B
F
E
D
C
B
A
P
P
8
7
6
5
4
3
2
1
一落.二靠.三移.四画
AB∥CD
A
B
C
D
E
F
在横格纸上画两条平行线AB、CD,再画直线EF与直线AB、CD相交(如下图)
7
5
1
2
3
4
6
8
a
b
c
探究一
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
平行线性质1:两直线平行,同位角相等.
如果两直线不平行,
上述结论还成立吗?
b
c
a
已知:如图, a// b .
那么 3与 2有什么关系?
两直线平行,同位角相等
∠3
探究二
平行线性质2:两直线平行,内错角相等.
1
2
3
a
b
C
解: a∥b,
∠1=∠2
( )
又 ∠1= (对顶角相等),
∠ 2 = ∠3.(等量代换)
c
2
3
1
a
已知:如图a//b,
那么 2与 4有什么关系呢?
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 4=180°(邻补角定义)
2+ 4=180°(等量代换)
探究三
平行线性质3:两直线平行,同旁内角互补.
C
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵ a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补)
平行线的性质:
例题 如图是一块梯形铁片的残余部分,量得
∠A=115 °,∠D=100°,梯形另外两个角分别是
多少度
解:因为梯形上.下底互相平行,
所以
A
D
B
C
梯形的另外两个 角分别是
1.如图,直线a∥b, ∠1=54°,那么∠2, ∠3, ∠4各是多少度
解:
∵ ∠1 =54° (已知)
∴ ∠2=∠1 =54°(_____________)
∵ a∥b(已知)
∴ ∠4=∠1=54°(_______________________)
∠2+∠3=180°(_______________________)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
1
2
3
4
a
b
与
对顶角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证:(1)DE∥BC ;(2) ∠C的度数
a
b
内错角相等,两直线平行
∠4
两直线平行,同位角相等
∠5
3.填空(1)如图1∵∠1= ∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=180( )
a
b
c
d
1
2
3
4
5
图1
两直线平行,同旁内角互补
(2)如图2∵∠A+ ∠D=180(已知)
∴______∥______( )
∴∠B+∠C=_____( )
A
B
D
C
图2
AB
CD
同旁内角互补,两直线平行
1800
两直线平行,同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个性质:
平行线的三个判定:
1.如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
2.如图:已知 1= 2
求证: BCD+ D=180
BC
内错角相等,两直线平行
两直线平行,同旁内角互补
BC
证明:如图
∵ 1= 2(已知)
∴AD∥_____( )
∵AD ∥_____(已证)
∴ BCD+ D=180( )
作业:第23页3题.4题.
下课了
