北师大版高中数学必修5第三章第3节《基本不等式》同步测试(Word含答案)
文档属性
| 名称 | 北师大版高中数学必修5第三章第3节《基本不等式》同步测试(Word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 266.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 19:28:04 | ||
图片预览


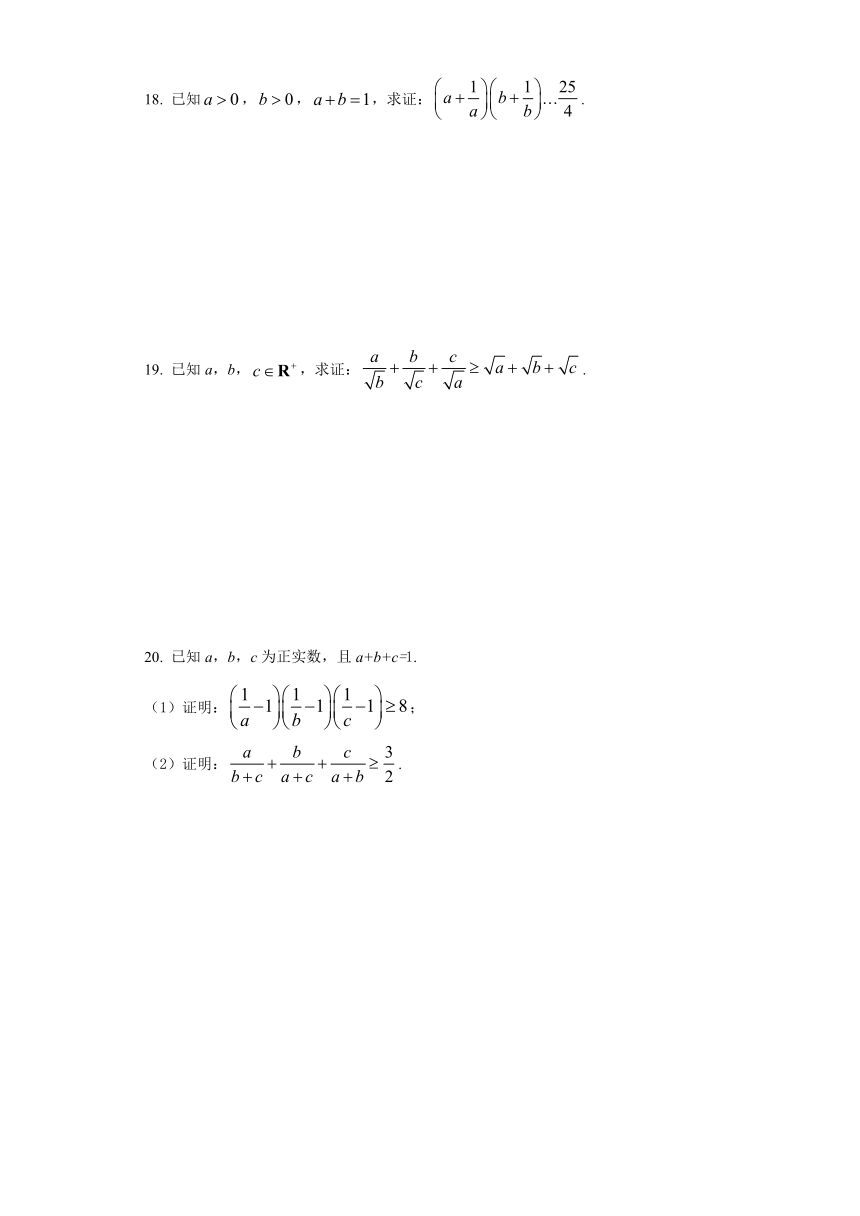
文档简介
《基本不等式》同步测试
一.选择题(本大题共12小题)
1.已知,则取最大值时的值为( ).
A.
B.
C.
D.
2.若,且,则下列不等式中,恒成立的是
A.
B.
C.
D.
3.若两个正实数满足,且存在这样的使不等式有解,则实数的取值范围是(
)
A.
B.
C.
D.
4.若,则的最小值等于(
)
A.6
B.9
C.4
D.1
5.设,满足,且,都是正数,则的最大值是(
)
A.4
B.2
C.40
D.20
6.已知
,且,若恒成立,则实数的值取值范围是(
)
A.
B.
C.
D.
7.若直线被圆截得弦长为4,则的最小值是(
)
A.9
B.4
C.
D.
8.设,为正数,且,则的最小值为(
)
A.
B.
C.
D.
9.设正实数,,满足,则当取得最小值时,的最大值为(
)
A.0
B.4
C.8
D.16
10.已知函数,(且)的图像恒过点,若直线经过点,则的最小值为(
)
A.
B.
C.
D.
11.直线与圆截得的弦长为4,则的最小值是(
)
A.3
B.2
C.
D.1
12.正数满足,若不等式对任意实数恒成立,则实数的取值范围是(
)
A.
B.
C.
D.
二.填空题(本大题共4小题)
13.若实数满足,则的最大值是____________.
14.已知,,且,则xy的最大值是________.
15.已知,则的最大值为________.
16.若正数,满足,则的取值范围是________.
三.解答题(本大题共6小题)
17.
已知,,且.
(1)求的最小值;
(2)证明:.
18.
已知,,,求证:.
19.
已知a,b,,求证:.
20.
已知a,b,c为正实数,且a+b+c=1.
(1)证明:;
(2)证明:.
21.
某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?
22.
南康某服装厂拟在年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)万件与年促销费用万元满足.已知年生产该产品的固定投入为万元,每生产万件该产品需要再投入万元.厂家将每件产品的销售价格定为每件产品年平均成本的倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将年该产品的利润万元表示为年促销费用万元的函数;
(2)该服装厂年的促销费用投入多少万元时,利润最大?
参考答案
一.选择题:本大题共12小题.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
C
B
B
D
A
D
C
C
B
D
二.填空题:本大题共4小题.
13.1
14.1
15.
16.
三.解答题:本大题共6小题.
17.【解析】(1),当且仅当“”时取等号,故的最小值为;
(2),
当且仅当时取等号,此时.故.
18.【解析】
,.
,,.
∴成立,故原不等式成立.
19.【解析】证明:,,,
当时等号成立,将以上三式相加,得.
20.【解析】(1),当且仅当“a=b=c”时取等号;
(2)
,
当且仅当“a=b=c”时取等号.
21.【解析】设水池的长为x米,则宽为米.
总造价:y=400(2x+)+100+200×60
=800(x+)+12000≥800+12000=36000,
当且仅当x=,即x=15时,取得最小值36000.
所以当净水池的长为15m时,可使总造价最低.
22.【解析】(1)由题意知:每件产品的销售价格为,
;
(2)由,
当且仅当,即时取等号.
答:该服装厂年的促销费用投入万元时,利润最大.
一.选择题(本大题共12小题)
1.已知,则取最大值时的值为( ).
A.
B.
C.
D.
2.若,且,则下列不等式中,恒成立的是
A.
B.
C.
D.
3.若两个正实数满足,且存在这样的使不等式有解,则实数的取值范围是(
)
A.
B.
C.
D.
4.若,则的最小值等于(
)
A.6
B.9
C.4
D.1
5.设,满足,且,都是正数,则的最大值是(
)
A.4
B.2
C.40
D.20
6.已知
,且,若恒成立,则实数的值取值范围是(
)
A.
B.
C.
D.
7.若直线被圆截得弦长为4,则的最小值是(
)
A.9
B.4
C.
D.
8.设,为正数,且,则的最小值为(
)
A.
B.
C.
D.
9.设正实数,,满足,则当取得最小值时,的最大值为(
)
A.0
B.4
C.8
D.16
10.已知函数,(且)的图像恒过点,若直线经过点,则的最小值为(
)
A.
B.
C.
D.
11.直线与圆截得的弦长为4,则的最小值是(
)
A.3
B.2
C.
D.1
12.正数满足,若不等式对任意实数恒成立,则实数的取值范围是(
)
A.
B.
C.
D.
二.填空题(本大题共4小题)
13.若实数满足,则的最大值是____________.
14.已知,,且,则xy的最大值是________.
15.已知,则的最大值为________.
16.若正数,满足,则的取值范围是________.
三.解答题(本大题共6小题)
17.
已知,,且.
(1)求的最小值;
(2)证明:.
18.
已知,,,求证:.
19.
已知a,b,,求证:.
20.
已知a,b,c为正实数,且a+b+c=1.
(1)证明:;
(2)证明:.
21.
某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?
22.
南康某服装厂拟在年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)万件与年促销费用万元满足.已知年生产该产品的固定投入为万元,每生产万件该产品需要再投入万元.厂家将每件产品的销售价格定为每件产品年平均成本的倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将年该产品的利润万元表示为年促销费用万元的函数;
(2)该服装厂年的促销费用投入多少万元时,利润最大?
参考答案
一.选择题:本大题共12小题.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
C
B
B
D
A
D
C
C
B
D
二.填空题:本大题共4小题.
13.1
14.1
15.
16.
三.解答题:本大题共6小题.
17.【解析】(1),当且仅当“”时取等号,故的最小值为;
(2),
当且仅当时取等号,此时.故.
18.【解析】
,.
,,.
∴成立,故原不等式成立.
19.【解析】证明:,,,
当时等号成立,将以上三式相加,得.
20.【解析】(1),当且仅当“a=b=c”时取等号;
(2)
,
当且仅当“a=b=c”时取等号.
21.【解析】设水池的长为x米,则宽为米.
总造价:y=400(2x+)+100+200×60
=800(x+)+12000≥800+12000=36000,
当且仅当x=,即x=15时,取得最小值36000.
所以当净水池的长为15m时,可使总造价最低.
22.【解析】(1)由题意知:每件产品的销售价格为,
;
(2)由,
当且仅当,即时取等号.
答:该服装厂年的促销费用投入万元时,利润最大.
