湘教版九年级数学上册 3.4 相似三角形的性质和判定课件(第1课时 共19张PPT)
文档属性
| 名称 | 湘教版九年级数学上册 3.4 相似三角形的性质和判定课件(第1课时 共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
1.回忆全等三角形的性质:
两个全等三角形具有哪些性质?
往事新忆
全等三角形的
①对应角相等
②对应边相等
③对应高相等
④对应中线相等
⑤对应角平分线相等
展开想象的翅膀:
相似三角形的对应角、对应边、
对应高、对应中线及对应角平分线
有何关系?
对应角相等,对应边成比例。
我们来研究其它性质
J我们把对应边的比值称为相似比
猜想:
相似三角形对应高的比是否等于相似比
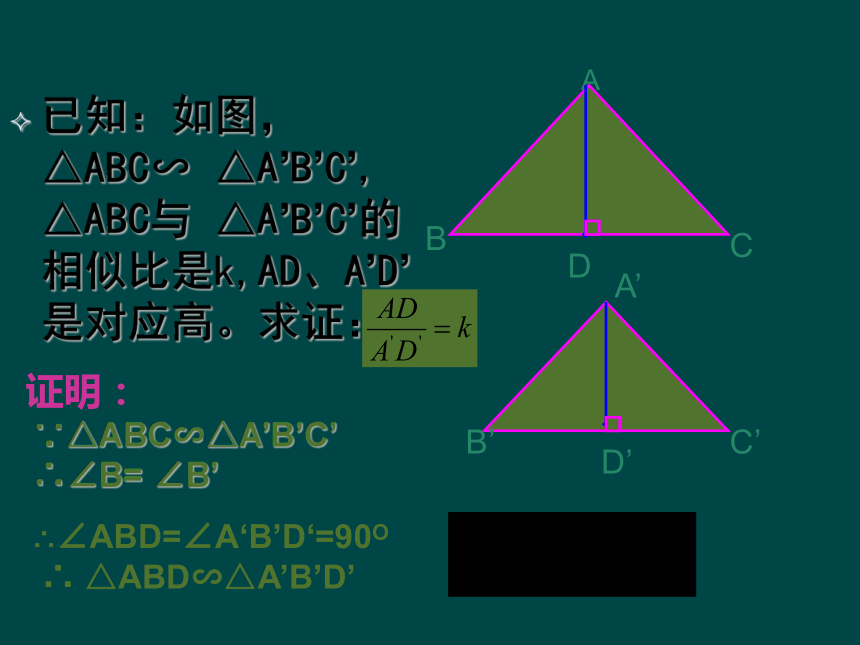
已知:如图,△ABC∽
△A’B’C’,
△ABC与
△A’B’C’的相似比是k,AD、A’D’是对应高。求证:
A
B
C
B’
A’
C’
D
D’
证明:
∵△ABC∽△A’B’C’
∴∠B=
∠B’
∴∠ABD=∠A‘B’D‘=90O
∴
△ABD∽△A’B’D’
定理:
相似三角形的对应高的比,对应中线的比与对应角平分线的比等于相似比。
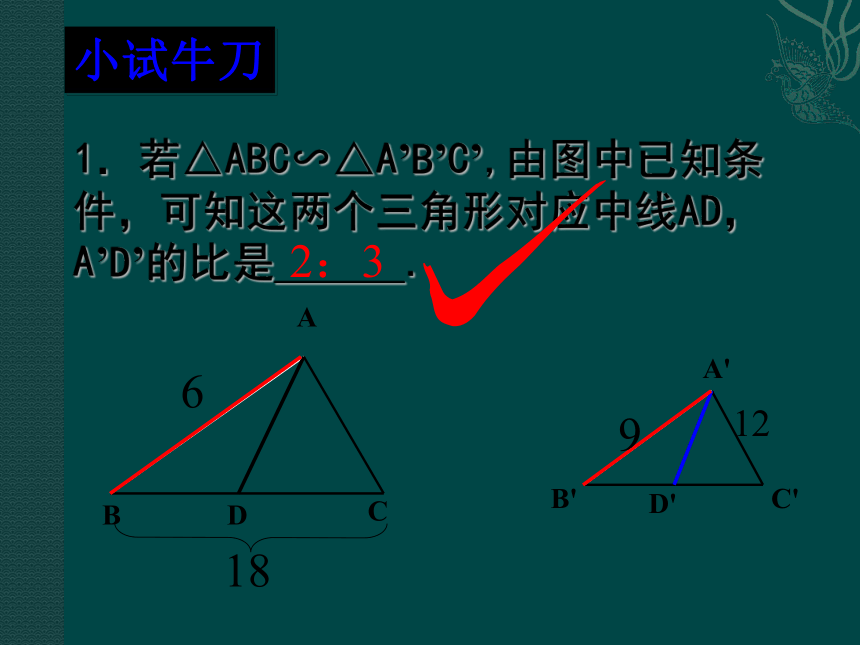
1.若△ABC∽△A’B’C’,由图中已知条件,可知这两个三角形对应中线AD,A’D’的比是
.
小试牛刀
2:3
A
B
C
D
B'
A'
C'
D'
6
9
18
12
2.若两个相似三角形对应高的比为1:3,则这两个三角形的的相似比是______
小试牛刀
1:3
3.△ABC∽△A’B’C’,AD和A’D’是
它们的对应角平分线,已知AD=4cm,
A’D’=10cm,那么对应高的比
是________
2:5
图中(1)(2)(3)分别是边长为1、2、3的
等边三角形,它们都相似?为什么?
(2)与(1)的相似比=________________,
?
(2)与(1)的周长比=________________;
?
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________,
?
(3)与(1)的周长比=________________.
?
(3)与(1)的面积比=________________.
?
由可以得出结论:
相似三角形的面积比等于
.
相似比
相似比的平方
1.相似三角形对应边的比为3∶5
,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。
变化:
相似三角形对应边的比为9∶8?
2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____,
周长比为___
.
3.两个相似三角形对应中线的比为1:4,则对应高的比为______
,面积比为______。
已知:
,
它们的周长分别为60cm和72cm,
且AB=15cm,
∽△
△
=24cm。
求:
BC,
AC,
A′B′,
A′C′
1、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。
例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为100cm2
,且
求四边形BCDE的面积。
1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12
,则较小三角形的周长____cm,面积为____
。
1:2
1:4
12
4/3
再见
Class
Over
1.回忆全等三角形的性质:
两个全等三角形具有哪些性质?
往事新忆
全等三角形的
①对应角相等
②对应边相等
③对应高相等
④对应中线相等
⑤对应角平分线相等
展开想象的翅膀:
相似三角形的对应角、对应边、
对应高、对应中线及对应角平分线
有何关系?
对应角相等,对应边成比例。
我们来研究其它性质
J我们把对应边的比值称为相似比
猜想:
相似三角形对应高的比是否等于相似比
已知:如图,△ABC∽
△A’B’C’,
△ABC与
△A’B’C’的相似比是k,AD、A’D’是对应高。求证:
A
B
C
B’
A’
C’
D
D’
证明:
∵△ABC∽△A’B’C’
∴∠B=
∠B’
∴∠ABD=∠A‘B’D‘=90O
∴
△ABD∽△A’B’D’
定理:
相似三角形的对应高的比,对应中线的比与对应角平分线的比等于相似比。
1.若△ABC∽△A’B’C’,由图中已知条件,可知这两个三角形对应中线AD,A’D’的比是
.
小试牛刀
2:3
A
B
C
D
B'
A'
C'
D'
6
9
18
12
2.若两个相似三角形对应高的比为1:3,则这两个三角形的的相似比是______
小试牛刀
1:3
3.△ABC∽△A’B’C’,AD和A’D’是
它们的对应角平分线,已知AD=4cm,
A’D’=10cm,那么对应高的比
是________
2:5
图中(1)(2)(3)分别是边长为1、2、3的
等边三角形,它们都相似?为什么?
(2)与(1)的相似比=________________,
?
(2)与(1)的周长比=________________;
?
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________,
?
(3)与(1)的周长比=________________.
?
(3)与(1)的面积比=________________.
?
由可以得出结论:
相似三角形的面积比等于
.
相似比
相似比的平方
1.相似三角形对应边的比为3∶5
,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。
变化:
相似三角形对应边的比为9∶8?
2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____,
周长比为___
.
3.两个相似三角形对应中线的比为1:4,则对应高的比为______
,面积比为______。
已知:
,
它们的周长分别为60cm和72cm,
且AB=15cm,
∽△
△
=24cm。
求:
BC,
AC,
A′B′,
A′C′
1、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。
例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为100cm2
,且
求四边形BCDE的面积。
1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12
,则较小三角形的周长____cm,面积为____
。
1:2
1:4
12
4/3
再见
Class
Over
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
